Ratio of Triangle Area in Folded Rectangle

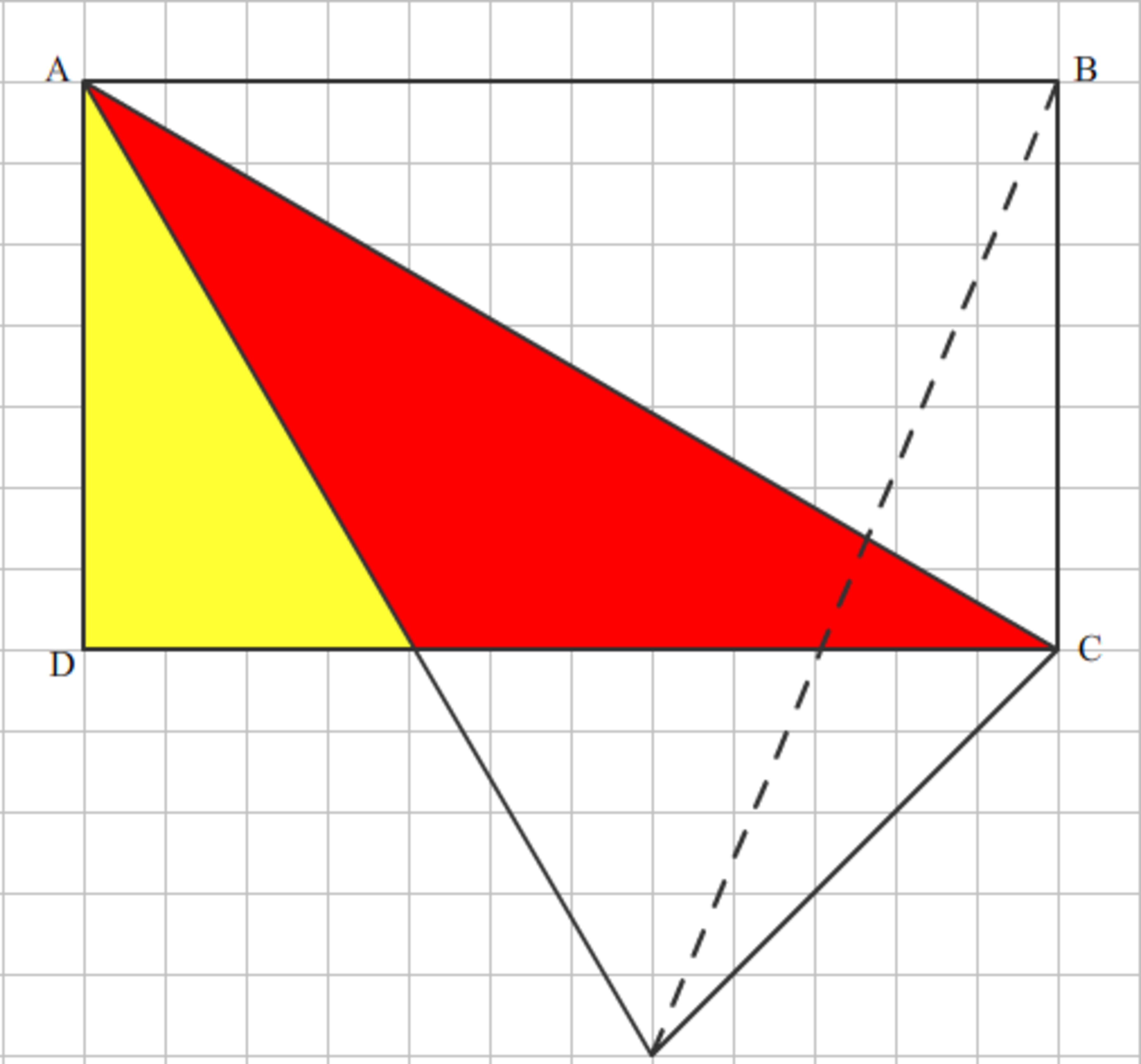
Hello again. I have a problem that occured over a year ago. But, I cannot solve it until now. The problem is: Given that the rectangle with length x and width y. This rectangle was folded based on its diagonal to form two triangles. Find the area ratio between red and yellow triangles! I've already tried to find it, but still don't get the solution. Maybe any theorems or formulas that I can use to solve this problems? Thanks

Note by Leonardo Chandra
8 years ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

First off, I think the graph is innacurate, because the botom angle is produced by a reflection of the top-right angle, which is 90 degrees. The bottom angle is not 90 degrees though. Let's not let that impede us though.

Here's my method of solving it. It is based on the double-angle formula for tangent. The slope of AC is −yx-\frac{y}{x}. Call the point on the bottom E, and the intersection of AE and DC point F. The duplication of ∠CAB\angle CAB onto ∠EAC\angle EAC produces ∠EAB\angle EAB, which the slope of AE is derived from.

My patience with LaTex is not good enough to write out all the algebra, but the slope of AE is −2xyx2−y2-\frac{2xy}{x^{2}-y^{2}}.

Next, DF is the run of line AE when the rise is −y-y Using the slope equation for AE, the run is x2−y22x\frac{x^{2}-y^{2}}{2x}. That is the base for the red triangle. The base for the yellow triangle is x−x2−y22x=x2+y22xx-\frac{x^{2}-y^{2}}{2x}=\frac{x^{2}+y^{2}}{2x}.

SInce we have found the two bases, and the height for the two is both y , the ratio of the red triangle to the yellow isx2−y2x2+y2\frac{x^{2}-y^{2}}{x^{2}+y^{2}}.

x2−y2x2+y2\frac{x^{2}-y^{2}}{x^{2}+y^{2}} is the answer.

Clarence Chen - 8 years ago

Is it supposed to be x and y, or specifically 7 and 12 ?

KATHLEEN KASPER - 8 years ago

Log in to reply

It states 'length x and width y' in the actual problem. I believe the diagram was posted so that we could see which triangles he was talking about.

Tim Ye - 8 years ago

yes, it's only tell me about the variables, x and y, no other specifics number. The picture were drawn not in the real measure, only approximation.

Leonardo Chandra - 8 years ago
×

Problem Loading...

Note Loading...

Set Loading...