Related Rates

Related rate problems take into consideration how a change in one quantity results in a change in another country. For example, when blowing up a balloon, the surface area of the balloon is changing, and so is the volume of the balloon. The rate at which the volume out these problems of the balloon changes will determine the rate at which the surface area of the balloon is changing. The two rates are related. In working out these problems, the chain rule is essential.

Here is a basic problem-solving strategy that may help when setting up related rates problems. Related rates problems usually involve functions that are changing with respect to time. It will be very important to identify the independent variable and write down appropriate formulas from geometry and trigonometry.

Read the problem carefully.

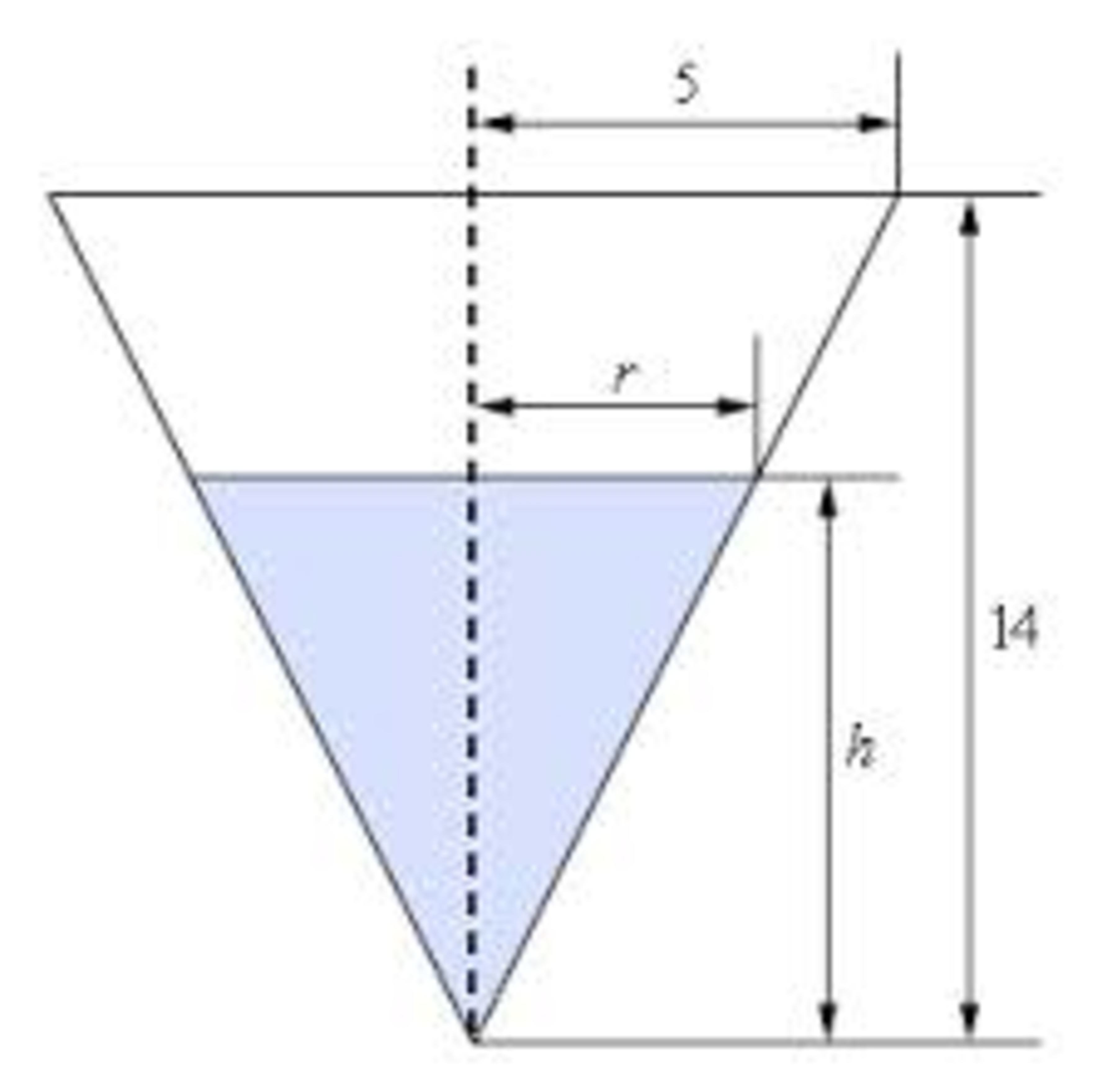
Draw a picture.

Identify the variables used to represent the quantities under consideration.

Interpret the rate information given as a derivative.

Write an equation that relates the various quantities involved in the problem. Use the geometry and trigonometry to relate some of the variables to each other to help eliminate them from the equation.

Differentiate the equation with respect to time by using the chain rule and then solve for the appropriate quantity.

Re-read the question to make sure that you have answered it completely.

#Calculus #RelatedRates

Note by Lew Sterling Jr
6 years, 7 months ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

There are no comments in this discussion.

×

Problem Loading...

Note Loading...

Set Loading...