Resolution Needed: 0^0=?

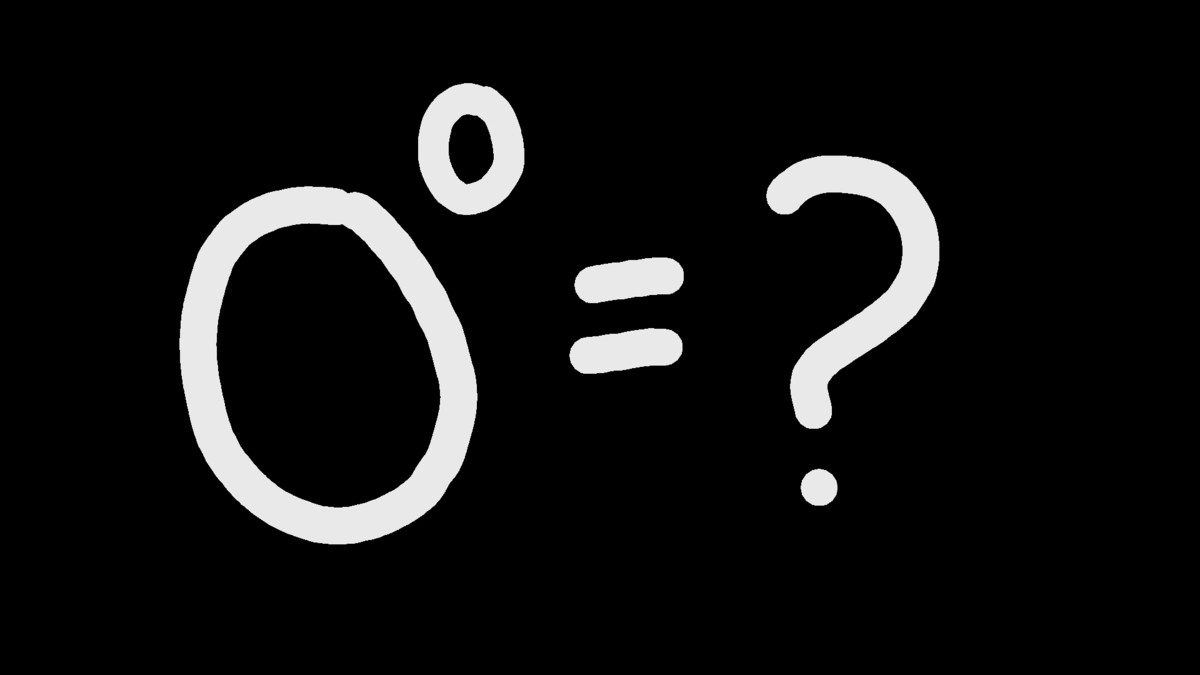
I've noticed that problems involving $0^{0}$ get a lot of reports and comments debating what the answer is. It seems that Brilliant members are divided into two sides: one saying it is indeterminate, the other saying it is $1$ .

I believe we need to come up with a collective agreement on what the value of $0^{0}$ is so that we avoid future chaos/confusion/conflicts. The purpose of this note is not to decide on the "right answer," but to decide how we can all compromise. What would be the best way to do this?

Please comment your opinion below. Thank you for reading this note!

#Algebra #Exponents #RealNumbers #Brilliant #0

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

I think it is indeterminate, waiting for the staff to give the opinion!

Swapnil Das - 6 years, 1 month ago

@Calvin Lin Mr. Lin, I would like to ask for your opinion on how this debate can be settled for problems posted on Brilliant in the future. Thank you.

Nadia Jo - 6 years, 1 month ago

I think we need to have a vote, I know some people do not have opinions, but maybe it would be okay for this to be done on a problem by problem basis. If a problem requires the solution of 0 to the 0 and they do not want it to be 1 or indeterminate(whichever we decide to make as the basis) they can state in the problem what the definition of 0 to the 0 is.

Rmflute Shrivastav - 6 years, 1 month ago

Well, many conventions defined $0^{0}$ as $1$ .

William Park - 6 years, 1 month ago

If you search "0^0" in Google, the Google calculator tells me that it's 1. Of course, I can't completely trust Google's answer, but I think it's 1.

William Park - 6 years, 1 month ago

Again, this is NOT intended for discussing what the answer is. This is intended for discussing how we can all agree on an answer.

Nadia Jo - 6 years, 1 month ago

Okay... we should vote!

William Park - 6 years, 1 month ago

Ya!

Swapnil Das - 6 years, 1 month ago

@Swapnil Das – @Calvin Lin Is it possible to have a vote?

William Park - 6 years, 1 month ago

@William Park – I guess, he will allow it!

Swapnil Das - 6 years, 1 month ago

Well, Youtube sources say that it is undefined, including the numberphile. Further, it's proof has also been derived by calculus.

Swapnil Das - 6 years, 1 month ago

I think it should be 1

Jahnvi Verma - 6 years, 1 month ago

Indeterminate. For textbooks that consider real number arithmetic only, it is often convenient to just define 0^0=1 however.

Bejoy Sen - 6 years, 1 month ago

Google says 1... But Wolfram Alpha says indefinite.

Jules Le Menestrel - 6 years, 1 month ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$