Restricted Proof Challenge : Combinatorics

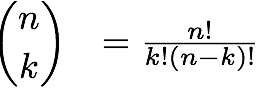
Here's the challenge.

Prove that $n$ choose k, $\binom{n}{k} = \frac{n!}{(n-k)!k!},$ is always an integer. However, you are not allowed to use the fact that this is an integer counting function ie. that this is the way of choosing $k$ objects from a set of $n$ objects and therefore an integer.

Leave a proof in the comments :)

#Combinatorics #Proofs #Nchoosek

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Let's suppose that all coefficients for a particular $n$ are integers. Check how this goes

$\dfrac { n! }{ k!(n-k)! } +\dfrac { n! }{ (k-1)!(n-k+1)! } =$

$\dfrac { n! }{ k!(n-k)! } +\dfrac { n!k }{ k!(n-k)!(n-k+1) } =$

$\dfrac { n! }{ k!(n-k)! } \left( 1+\dfrac { k }{ n-k+1 } \right) =$

$\dfrac { n! }{ k!(n-k)! } \left( \dfrac { n+1 }{ n-k+1 } \right) =$

$\dfrac { n! }{ k!(n-k)! } \left( \dfrac { n+1 }{ n+1-k } \right) =$

$\dfrac { (n+1)! }{ k!(n+1-k)! }$

We've proved by induction that the coefficients for $n+1$ are also all integers. Etc.

Michael Mendrin - 5 years, 8 months ago

Nice one :) Can you see an intuitive reason why it is an integer (with the restriction still applying) ? I feel like I am missing something obvious.

Roberto Nicolaides - 5 years, 8 months ago

The sum of two integers is an integer. The assumption is that for all coefficients for a particular $n$ are already integers. This then proves that they're all integers for $n+1$ . I can spend more time making this more rigorous, but the essential point is the same. Pascal triangle, remember? If one row is all integers, then so is the next.

I suppose you'd like a proof where we can't start with the assumption that any of them are integers?

Michael Mendrin - 5 years, 8 months ago

@Michael Mendrin – The induction argument is great :) But yeah, a proof with out assumption that any of them are integers is what I'm secretly looking for. I'm still always a little surprised that the denominators divide into the numerators every time! This doesn't seem intuitive to me when I just look at the formula. Is this the case for most people?

Roberto Nicolaides - 5 years, 8 months ago

@Roberto Nicolaides – I know what you mean. If one isn't familiar with Pascal's triangle, and you're just shown a fraction with factorials in it, how is it that it's an integer every time? Proving it directly takes a bit of effort. It becomes an tedious effort of chasing down the primes, like trying to herd cats.

Michael Mendrin - 5 years, 8 months ago

Let's make $k<= \frac{n}{2}$ .

$\binom{n}{k} = \frac{n!}{(n-k)!k!} = \frac{(n-k+1)(n-k+2)...(n-1)n}{(k)!}$

We have numbers $(n-k+1) \text{ through } n$ in the numerator and $1 \text{ through } k$ in the denominator, $k$ numbers in both cases. Consecutive natural numbers will have its multiples in the range $(n-k+1) \text{ through } n$ which will make it possible for them to simplify. In other words, any set of $k$ consecutive natural numbers will contain multiples of first $k$ natural numbers.

It would be intuitive approach to understand why, not exactly the full proof.

Maria Kozlowska - 5 years, 8 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$