Right triangle and two parallelograms
This is the first problem of #PeruMOTraining, you can see my first post here. I proposed this problem for the Peruvian Mathematical Olympiad, in 2011. Please post your solutions!
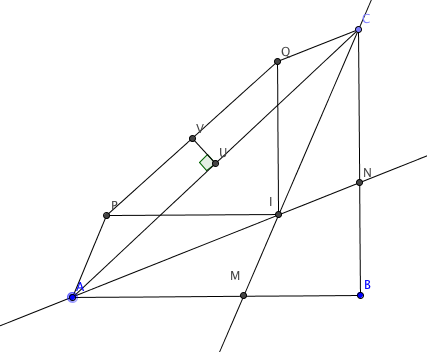
Problem Let be a right triangle, with . Let and be interior bisectors intersecting at ( is on the segment and is on the segment ). Construct the paralellograms and . If and are the midpoints of segments and , respectively. Prove that and are perpendicular.
No vote yet
1 vote
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
Let's assume AB=a, BC=b and CA=c. X is the point so that VX is parallel to AB and UX is parallel to BC. So VXU is a right triangle at X. Let r be the inradius of ABC, so r = (a+b-c)/2. Let's calculate VX and UX.
VX = (1/2)IP + r - (1/2)AB = (1/2) (AM + 2r - a) = (1/2) (AM + (b-c))
By the angle bisector theorem AM/MB = c/b, so AM/a=c/(b+c), or AM = ac/(b+c) . Hence
(b+c)(AM + (b-c)) = ac + (b^2-c^2) = ac - a^2 = a(c-a) = a(c-a)(c+a)/(a+c) = ab^2/(a+c)
So 2(a+c)(b+c)VX = ab^2 Similarly 2(a+c)(b+c)UX = ba^2
So VX/UX= b/a = CB/AB. Hence VXU is similar to CBA. This should be enough to conclude UV is perpendicular to AC.
Log in to reply
Please, can you explain why VX=(1/2)IP+r−(1/2)AB ?
Log in to reply
The (distance from V to BC) is the (distance from V to IQ) + the (distance from I to BC)
The (distance from V to IQ) = (1/2)IP
The (distance from I to BC) = r
The (distance from U to BC) = (1/2)AB
VX = (distance from V to BC) - (distance from U to BC)
Wow I'm so happy that the new features have given us not only geometry problems, but also more discussions.
This is a very nice problem here I will give a synthetic solution:
Let's take advantage of all these midpoints. We construct a point on rayAV such that V is the midpoint of AK.Now we have VU∥CK, which means we just have to prove CK⊥AC. Moreover, we get parallelogram APKQ so QK=MI,IN=QC,∠KQC=∠CIN=45. Now since ∠QCA=∠CAN=∠NAB, therefore CK⊥AC is equivalent to proving ∠KCQ=90−∠QCA=90−∠NAB=∠ANB. Since ∠KQC=45=∠NBI, thus we just have to prove △KQC∼△IBN or simply BNBI=QCQK=INMI. This is indeed true from △MIB∼△INB and here's its proof: since ∠AIM=∠ABI=45, therefore ∠NIB=∠IAM+∠IBA=∠IAM+∠AIM=∠IMB. It's already known that ∠IBM=∠IBN, so that gives us the similarity. □
I haven't been keeping up with all these posts lately, wish I had found this sooner. :)
Log in to reply
Nice solution Xuming! You find another property of a right triangle: triangles MBI and IBN are similar!
Log in to reply
I actually have a few more. I found them while trying different constructions of points and lines.
The following is a nice property about a right triangle.
[Keeping the same notation of our problem]
Property
The projections of the segments MI and IN on the line AC have the same length.
Proof Let E and F in AC such that ME and NF are perpendicular to AC. Denoting d(X,YZ) the distance from point X to line YZ, we have d(I,ME)=d(I,MB)=r=d(I,NB)=d(I,NF) . Since d(I,ME) is the length of the projection of MI on the line AC and d(I,NF) is the length of the projection of NI on the line (AC), we are done!
Could you use this property to solve our problem?
Log in to reply
OK, so if X, Y are on AC such that both PX and QY are perpendicular to AC, what you proved above implies that AX=CY as both are projections of AP and CQ onto AC. Hence U is the midpoint of XY. Since V is the midpoint of PQ, VU is parallel to PX. Hence VU is perpendicular to AC.
Log in to reply
The lemma seems to be unnecessary. Let X and Y as above, then ∠PAX=∠ACM=2C. So AX=APcos2C=IMcos2C=r. Similarly CY=r. The rest is the same as above.
Log in to reply
Basically the lemma states that AX=CY. My idea was to stand out a property concerning the points M, I, N without mention the other points.
Log in to reply
Yes, Thank you. A proof along that line was not possible for me without seeing your lemma.
Are we allowed to use co-ordinate geometry? I thought of a solution using co-ordinate geometry but it is turning out to be a bit ugly.
Log in to reply
I believe so. All solutions are welcome.
Since we have a right angle, a solution with co-ordinate geometry seems possible.
Log in to reply
Yes, I did with coordinates too, finding the coordinates of V is pretty much same as what I posted above. Then it's just a matter of verifying the slope of VU is the negative reciprocal of the slope of AC.
Please post a solution that is understandable and graceful......... I'm still in Middle School
AC is parallel PQ UV &AC are perpendicular
Log in to reply
In general, AC and PQ are not parallel.
Even AC and PQ are parallel can't conclude that VU and AC are perpendicular unless AP=CQ which is clearly not true.
Log in to reply
And AP=CQ implies that it's a 45-45-90 triangle... I'm posting this so we can have 3 people from San Diego replying to the same post. :) Such a rare scene.
Best and shortest solution here I think.