RMO 2013 problem

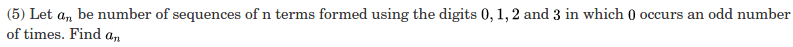
Could someone please help me with the attached RMO 2013 problem?

I got the answer to be $3^{n-1}n + [\frac{n-1}{2}]$, where the square brackets, [], imply the floor function. Is that right? I couldn't find an answer key for this (Maharashtra and Goa) anywhere.

Any help will be highly appreciated.

#NumberTheory #Sequences #RMO

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

I'm getting $2^{n-1}(2^n - 1)$ .

Siddhartha Srivastava - 5 years, 6 months ago

Could you please explain?

Shashank Rammoorthy - 5 years, 6 months ago

Let $b_n$ be the number of sequences formed which have an even number of zeros.

Then it is obvious that $4^n = a_n + b_n$ , since there $4^n$ sequences of $n$ terms, and each sequence must contain an even or odd number of zeroes.

Now, look at any sequence part of $a_n$ . It's first term is either zero (1 way), or not zero (3 ways). If the first term is zero, the remaining sequence must contain an even number of zeroes, and thus is $b_{n-1}$ . Likewise, if the first term is not zero, the remaining sequence is $a_{n-1}$ .

Therefore, $a_n = b_{n-1} + 3a{n-1}$ . Eliminating $b _n$ from both equations, we have

$a_n = 2a_{n-1} + 4^{n-1}$

or $a_n = 6a_{n-1} -8a_{n-2}$

Solving this recurrence relation, using $a_1 = 1, a_2 = 6,$ , we get $a_n = 2^{n-1}(2^n - 1)$

Siddhartha Srivastava - 5 years, 6 months ago

@Siddhartha Srivastava – Thanks!

Shashank Rammoorthy - 5 years, 6 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$