RMO 2014 Delhi Region Q.4

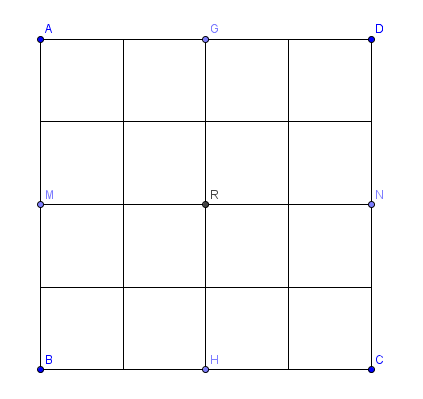
Is it possible to write the numbers $17,18,19,\ldots ,32$ in a $4\times 4$ grid on unit squares, with one number in each square, such that the product of the numbers in each $2\times 2$ sub-grids $AMRG, GRND, MBHR$ and $RHCN$ is divisible by 16?

You can find rest of the problems here
You can find the solutions here

#Combinatorics #NumberTheory #RMO #Divisibility

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

The answer is - impossible. Let us multiply all the numbers from 17 to 32 (the product will be equal to the product of four results for the sub-grids). It can easily be shown that the highest power of 2 in the product be 16. But as the number 32 (=2^5) should get in one of the sub-grids, the resultant 11th power of 2 should be distributed among three other grids. But it means that at least one of the products of the last three grids cann't be divisible by the fourth power of 2 equal to 16.

Сергей Кротов - 6 years, 6 months ago

yes , $2^{4} =16$

First let us write the prime factorization of all the even numbers ,

$18 = 2 * 9$

$20 = 2^{2} * 5$

$22 = 2 * 11$

$24 = 2^{3} * 11$

$26 = 2 * 13$

$28 = 2^{2} * 7$

$30 = 2 * 15$

$32 = 2^{5}$

The product of the numbers in 2x2 square to be divisible by 16 , each square should contain at least 2 raise to the power 4 . thus if in one 2x2 square if only 32 and other odd numbers is there - its satisfys . similarly - (18 , 20 ,22) , (20 ,28) ,(18 , 22 , 26 ,30) etc

sandeep Rathod - 6 years, 6 months ago

Nope If u place 32 in one of the sub grids u still need 12 factors of 2 (to be placed in the 3 other sub grids)but we are left with only 11 factors so such an arrangement is not possible

Aneesh Kundu - 6 years, 6 months ago

Yes, I tried combinations, but all fell in vain.

Ritu Roy - 6 years, 6 months ago

Oh yes sorry i used 18 2 times Thank you . How much you are expecting to get right?@Aneesh Kundu

sandeep Rathod - 6 years, 6 months ago

@Sandeep Rathod – I solved 4

Don't know how many are correct

Aneesh Kundu - 6 years, 6 months ago

We have $18=2\times9$ , $20=2^{2}\times5$ , $22=2\times11$ , $24=2^{3}\times3$ , $26=2\times13$ , $28=2^{2}\times7$ , $30=2\times15$ , $32=2^5$ .

I will consider the set of powers of 2, $A$ = ${1,2,1,3,1,2,1,5,0,0,0,0,0,0,0,0}$ ( $0$ corrsponds to the power of $2$ in the odd numbers).

Suppose we can partition the set $A$ into $4$ subsets $X_{1},X_{2},X_{3},X_{4}$ where $|X_{i}|=4$ where $i=1,..,4$ such that $k_{i}≥4$ where $k_{i}$ denotes the sum of the elements of $X_{i}$ .

Note that the sum of the elements of $A$ is $16$ .

Clearly ${5}$ belongs to one of the $4$ subsets,say $X_{1}$ .Then $k_{1}≥5$

Hence, $k_{2}+k_{3}+k_{4}=16-k_{1}≤11$ contradiction!(since sum of them is $≥12$ )

So, the arrangement given in the problem is impossible.

Souryajit Roy - 6 years, 6 months ago

it would have been possible if we had one number having 2^1 . by the way .. i got problems 1 ,4 right . it was my first experience in rmo . . .

Nihar Mahajan - 6 years, 6 months ago

I solved it using pigeon hole principle

Sauditya YO YO - 6 years, 5 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$