RMO 2016 Delhi Region
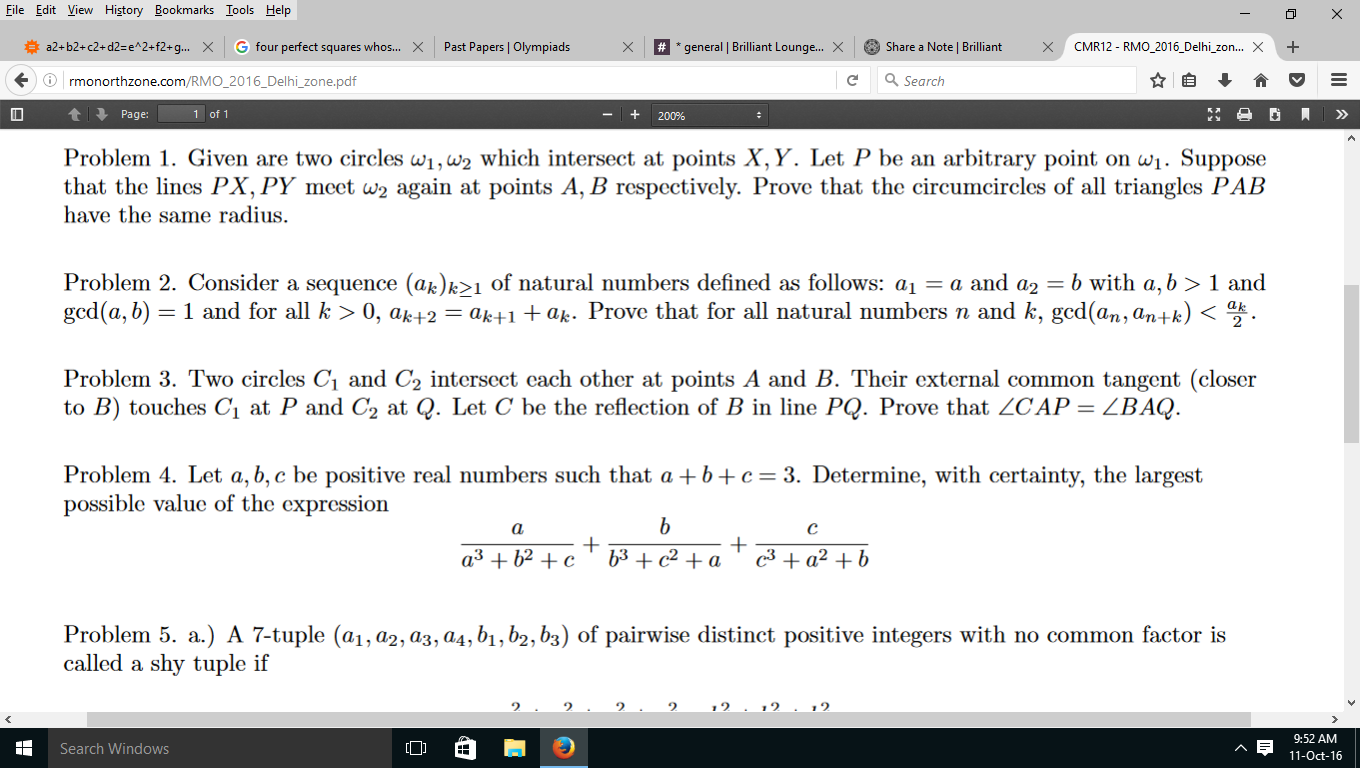
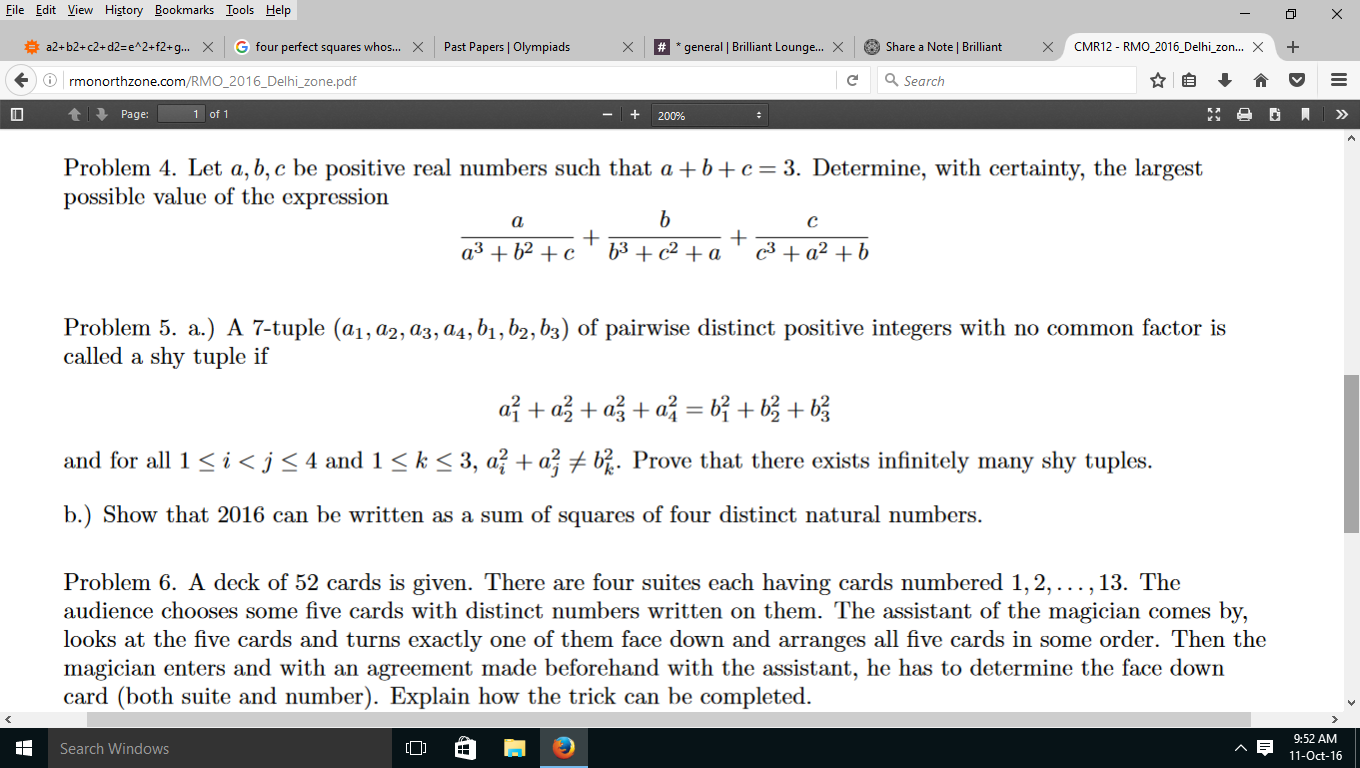
Here is the paper of RMO 2016 Delhi.Pls post answers and solutions to all questions. Also tell ur marks and estimated cut off Thanks!
No vote yet
1 vote
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
We can see that as we move the point P on the circumference of the circle[excluding X and Y],the ∠XPY=∠XP1Y remains constant.So this shows that AB=A1B1.Now we use extended sin rule to complete the problem.
Let the circum-radius of △PAB be R and △P1A1B1 be R1.
In △PAB,sin∠PAB=2R and in △P1A1B1,sin∠P1A1B1=sin∠PAB=2R1. Therefore 2R=2R1⇒R=R1.Hence Proved.
Log in to reply
nice solution
Hey can u explain in detail why A1B1=AB
Log in to reply
Because angle subtended by both of these chords at centre are equal. angle A1 X A =P X P1=P Y P1=B Y B1
Log in to reply
Which class are u in and which school?
Log in to reply
I am graduating from IIT Bombay. What is ur favourite college bro?
Log in to reply
IIT Is the one Bombay ,Perhaps
Log in to reply
Prefered Jee rank?mine was 17
Log in to reply
Hi Where Can I find some good material for RMO this year? Last time I failed miserably :'( could solve just one... Thanks :)
Log in to reply
would u like to join my RMO/INMO group. if yes then give ur email.
Log in to reply
Yeah he is good.Invite him
Log in to reply
what about u?
Log in to reply
what about me?
Log in to reply
wont u join our group?
Log in to reply
he is already in there @ayush rai
is dis question addressed to me?
My email [email protected] Sorry for the late reply I do not often open up Brilliant Thanks!!!
My email is [email protected] I know that this is a really late reply but I didn't know about it earlier ;)
first solve all previous year question papers, then use brilliant if ur aspiration is limited to rmo not inmo or selection camp P.S. i did 4 at my time
Do u remember books you used for iit preparation.I am an iit aspirant
Log in to reply
hcv,Bmsharma,resnick,irodov,krotov,kolenkow -Phy atkins,rc mukerje,bahadur,jd lee-Chm sl loney,hallknight,mostly tatamcgraw buks and tons of practise question papers here at allen.u can download them online also.Ncert is must .Hope it helps.
I m in class 10 And from bbps dw. But ur profile says u live in noida
Problem 5 1)its the easiest- use the identity (x+y+z)2+(x+y−z)2+(x−y+z)2+(−x+y+z)2=(2x)2+(2y)2+(2z)2 which gives infinite solutions in integers x,y,z.u can check it satisfis all other cond.s 2)solve this one other way round, assume 2016 = (2x)2+(2y)2+(2z)2 then it implies 504 = (x)2+(y)2+(z)2 by inspection x=22 y=4 z=6, then use the identity Problem 2 -we obtain nth term in terms of n,a,b then use strong induction.
Log in to reply
the question says pairwise distinct positive integers with no common factor, doesn't that mean they're pairwise coprime?
Log in to reply
The question mentions that they all don't have a factor in common, and that doesn't mean they are pairwise relatively prime. If x,y, and z are relatively prime, then we are done because then the gcd of these 7 terms would be 1 :)
Log in to reply
oh, thank you i didn't understand the question properly then
Can anyone post complete solution to 2nd and last problem?
Problem 4
By the Cauchy-Schwarz inequality, (a1+1+c)(a3+b2+c)≥(a+b+c)2=9
⟹(ac+a+1)(a3+b2+c)≥9a
Thus, we get
f(a,b,c)=∑(ac+a+1)(a3+b2+c)(ac+a+1)a≤∑9aa(ac+a+1)
⟹f(a,b,c)≤91[(ac+a+1)+(ba+b+1)+(cb+c+1)]
=91[(a+b+c)+(1+1+1)+(ab+bc+ca)]≤91[3+3+3]=1
Here we used the identity (a+b+c)2≥3(ab+bc+ca) to get ab+bc+ca≤3
Solution to Problem 1. Let P1 and P2 be the two points on ⊙ω1 as P varies across the circumference of ⊙ω1. Similarly, let P1X and P1Y meet ⊙ω2 at A1 , B1 and P2X and P2Y meet ⊙ω2 at A2 , B2 respectively.
Clearly , ∠XP1Y=∠XP2Y and ∠XB1Y=∠XB2Y
Adding these two eqn we get:: ∠A1XB1=∠A2XB2 => A1B1=A2B2.
Also, ΔXP1Y∼ΔA1P1B1 => RadiusA1P1B1RadiusXP1Y = A1B1XY ........[ 1 ]
Similarly, ΔXP2Y∼ΔA2P2B2
=> RadiusA2P2B2RadiusXP2Y = A2B2XY
=> RadiusA2P2B2RadiusXP1Y = A1B1XY ........[ 2 ]
[Because ΔXP1Y and △XP2Y have the same circumcircle. & A1B1=A2B2]
From eqn [1] and [2] we get that :: Radius A1P1B1 = Radius A2P2B2.
K.I.P.K.I.G
Diagram to problem 1.........
Log in to reply
Can anyone give complete solution of 2 and 6
Log in to reply
@Azimuddin Sheikh At least two cards have same suit let P1, P2 has same suit then the assistant will turn down one of P1, P2 (say P1) and arrange P2, P3, P4, P5 in such a way that P2 takes first position so the magician know that the card turned down and the card having first position have same suit. This will help him to identify suit of P1 now there are 6 ways to arrange P3 P4 P5 as LMH, LHM, MLH, MHL, HLM, HML (low number, middle number, high number) If difference of numbers obtained on P1 and P2 is 6 then turn down the higher one and give first position to lower one. Let us assume P1 has number k and P2 has no k + 1, k + 2, k + 3, k + 4, k + 5 or k + 6. If P2 has k + 1 then show LMH. If P2 has k + 2 then show LHM and soon. If difference is > 6 then turn down lower one and give first position to higher one and add 1,2,3,4,5,6 for arrangements LMH, LHM, MLH, MHL, HLM, HML in the higher number for example adding 4 to 11 indicates 2.
Log in to reply
The last combinatorics question is more or less the same as the first question in the chapter combinatorics from the book 'The art and craft of problem-solving'
@Azimuddin Sheikh Idk latex so cant post soln to 2
Pls do provide the solution of the last problem
Diagram to problem 3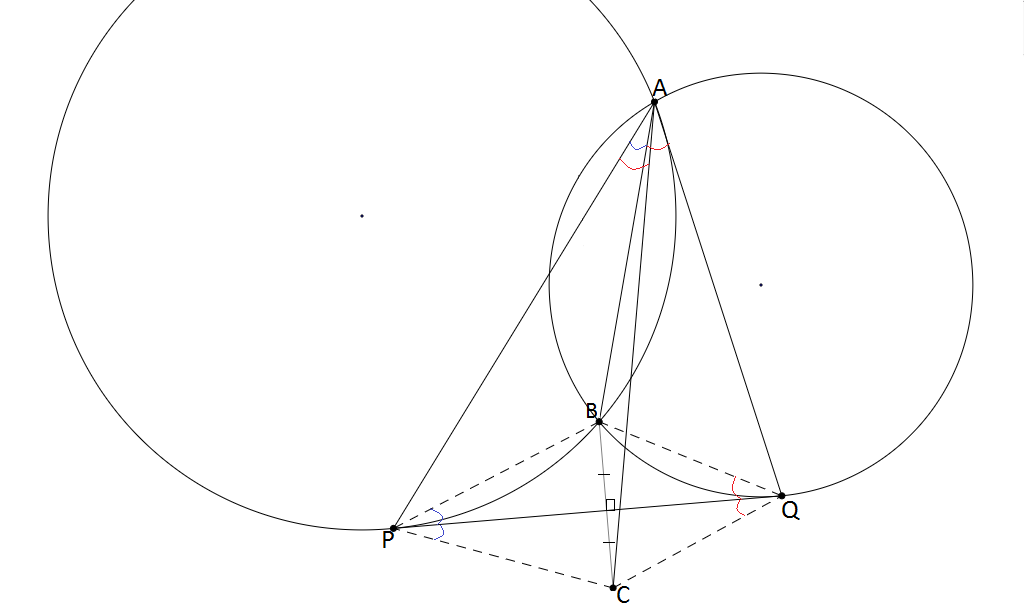
Log in to reply
Instead,use A-Humpty point lemma, which proves it without anything.
Log in to reply
Yup, and then repeat the same procedure to prove the lemma in examination.
Log in to reply
So in exam, to do any inequality, we can use only upto am-gm? not even cauchy? or can we not use even weighted am-gm?
Log in to reply
Hm... All those words go above me. Humpty-Dumpty theorem (Both different) are well-known. Although not that standard to be used directly in exams. I have seen guys proving each and every lemma, all for the sake of marks only/.
Log in to reply
so by standard textbooks, do they mean ncert?
Log in to reply
What? No.......
You can use AM-GM and weighted AM-GM because at times some problems are not easy to prove without weighted AM-GM{RMO 2012 paper1 p3}. Use Cauchy-Schwarz too because it is of the basic inequalities. If you use a lemma like the Titu's lemma, then better prove it for RMO, I guess no need to prove that in INMO, not IMO definitely!
Solution to 3
Const:-- Join BP , BQ , CP & CQ.
Clearly, Using Alternate Segment Theorem , we get:∠BAQ=∠BQP and ∠BAP=∠BPQ.--- [1]
Also Using the isosceles triangle property, we get :: ∠PQC=∠BQP & ∠QPC=∠BPQ-----[2]
Thus from eqn [1] and [2] we get: ∠BAQ=∠PQC & ∠BAP=∠QPC.
Adding these two results we get: ∠BAQ+∠BAP = ∠PQC+∠QPC
Thus ∠PCQ = 180∘−[∠PQC+∠QPC] = 180∘−[∠BAQ+∠BAP]
Therefore, ∠PCQ+PAQ = 180∘−[∠BAQ+∠BAP]+[∠BAP+∠BAQ] = 180∘
=>APCQ is cyclic
=> ∠PAC=∠PQC=∠BAQ
=> ∠PAC=∠BAQ
Need a solution for q 2 and 6
Please explain the statement above the concluding statement