RMO Board Part 2

Since the previous board was overcrowded with comments , I decided to create a new note so as to keep this step lively. If this also gets crowded , eventually we will again have new RMO board.What you have to do:

1) Propose a problem in the comments. Then I will add that problem here in this note content by giving the respective credit. And after I add the problem , the comment of proposing the problem must be deleted by the problem poster.

2) The problem poster must not post solution to his/her own problem unless someone from our community posts or no one gets it right even after considerable period of time.

3) Inappropriate / trivial comments are not allowed and must be deleted if posted by chance.An enthusiastic discussion is expected.

4) Please reshare this note so that we can reach most of the Brilliantians.

5)The problems to which solutions are posted will be accompanied by a checkmark $\large(\checkmark)$ at the end.

Problems:

Q1) Find all prime numbers $p$ for which there are integers $x,y$ satisfying $p+1=2x^2$ and $p^2+1=2y^2$ . $\large\checkmark$

Q2) The roots of the equation $x^3-3ax^2+bx+18c=0$ form a non-constant arithmetic progression and the roots of the equation $x^3+bx^2+x-c^3=0$ form a non-constant geometric progression. Given that $a,b,c$ are real numbers, find all positive integral values $a$ and $b$ .(Shared by Mycobacterium Tuberculae) $\large\checkmark$

Q3) In an equilateral $\Delta ABC$ , $P$ is a point inside the triangle such that $PA^2=PB^2+PC^2$ .Prove that $m\angle BPC = 150^\circ$ .(Shared by Raven Herd) $\large\checkmark$

Q4) Evaluate $\large\binom{n}{0} + \binom{n}{3} + \binom{n}{6} + \binom{n}{9} + ... \binom{n}{n}$ with respect to $n$ . (Shared by Svatejas) $\large\checkmark$

Q5) Consider a cyclic quadrilateral $ABCD$ such that $AC$ is the diameter of its circumcircle. Construct points $A'$ and $C'$ on $BD$ such that $AA' \perp BD$ and $CC' \perp BD$ . Show that $DA'=C'B$ .(Shared by Karthik V)

Q6) Prove that polynomial $az^n+z+1$ has at least one root in $|z|\leq 2$ . (Shared by Shivamani P)

Q7) If $a,b,c$ are positive reals , determine the minimum value of the expression $ab(a-c)+bc(b-a)+ca(c-b)$ with proof. (Posed by Nihar M) $\large\checkmark$

Q8)a) How many ways are there to represent a natural number $n$ as a sum of $k$ natural numbers?

Q8)b) How many ways are there to represent a natural number $n$ as a sum of $k$ non-negative numbers?

Q9) Find all ordered pairs of integers $(m,n)$ satisfying: $3\times 2^m + 1= n^2$ .

Q10)a) Prove that if $x^2+px-q$ and $x^2-px+q$ both factorize into linear factors with integral coefficients, then the positive integers and are respectively the hypotenuse and area of a right angled triangle sides of integer lengths.

Q10)b) Show further that if $x^2+px-q = (x-\alpha)(x-\beta) \ and \ x^2-px+q = (x-\gamma)(x-\delta)$ where $p,q,\alpha,\beta,\gamma,\delta$ are integers, $\alpha,\beta,\gamma,\delta$ then are numerically the radii of the incircle and the three excircles of the triangle. (Shared by Svatejas S)

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Q4) Let $f(x) = (1+x)^{n} ={n \choose 0}+ {n \choose 1} x + \ldots + {n \choose n} x^{n}$

Now, $f(1) + f(\omega) +f(\omega ^2) = {n \choose 0} (1+ \omega + \omega ^2) + {n \choose 1} (1+ \omega ^{2} + \omega ^{4}) + \ldots + {n \choose n} (1+ \omega ^n + \omega ^2n)$ $= 3 \left( {n \choose 0} + {n \choose 3}+ {n \choose 6} + \ldots \right)$

So, ${n \choose 0} + {n \choose 3}+ {n \choose 6} + \ldots = \dfrac{f(1) + f(\omega) +f(\omega ^2)}{3} = \dfrac{2^n + (- \omega ^2)^n + ( - \omega)^n}{3}$ .

So, we can manipulate the value of this expression by knowing the value of $n$ .

Surya Prakash - 5 years, 8 months ago

@Surya Prakash Great job!! Can you simply this further to eliminate $\omega$ ?

A Former Brilliant Member - 5 years, 8 months ago

Q1) It is clear that $p(p-1) = 2(y+x)(y-x)$ . If $p|y-x$ it implies that $p \leq y-x$ , then it should imply that $p-1 \geq 2(y+x)$ . But it is not possible. So, $p$ does not divide $y-x$ . So, $p|y+x$ it implies that $p \leq y+x$ , but this implies that $p-1 \geq 2(y-x)$ . So, we get $p +1 \leq 4x$ . Which reduces to $2x^2 \leq 4x$ , $x \leq 2$ . If $x=1$ , then $p=1$ , a contradiction. And $x=2$ implies that $p=7$ . Therefore, $p=\boxed{7}$ is the only solution.

For the $2nd$ question,

Let the roots of first equation be $m-d,m,m+d$

Therefore we get that, $m-d+m+m+d=3a=3m$ . Hence $m=a$

Then by applying Vieta's formula for other two, we get that, $3{m}^{2}-{d}^{2}=b$ and ${m}^{3}-m{d}^{2}=-18c$

Let the roots for the second equation be $n/r,n,nr$

Therefore by applying Vieta's fomula,we get that, $n=c$ and $n(1/r+1+r)=-b$ and ${n}^{2}(1/r+1+r)=1$

From here we get that, $n=-1/b=c$

Substituting these values in the previously acquired equations we get that, ${m}^{3}-m(3{m}^{2}-b)=18/b$

Simplifying we get that, $a{b}^{2}-2{a}^{3}b-18=0$

Applying formula for quadratic roots, $b=\frac{{a}^{3}\pm \sqrt{{a}^{6}+18a}}{a}$

For $b$ to be an integer, ${a}^{6}+18a={k}^{2}$

We see that, ${a}^{3}<k<{a}^{3}+3$

From here we see that, $a=2$ only satisfies. Therefore the required solutions are $a=2$ and $b=9$ .

Saarthak Marathe - 5 years, 8 months ago

My solution for the $3rd$ one is quite big. I will just give some hints to solve it.

Try it by co-ordinate geometry.
Take $B$ as $(-1/2,0)$ and $C$ as $(1/2,0)$ .Therefore,we get $A$ as $(\sqrt{3}/2,0)$ .
Then take $P$ as $(x,y)$ use the provided equation of ${PA}^{2}={PB}^{2}+{PC}^{2}$ to get the equation of locus of $P$ .The equation comes out to be ${x}^{2}+{y}^{2}+\sqrt{3}y-1/4=0$
Then take the $X-Y$ plane as the Argand plane and apply the Rotation theorem of Complex numbers for $B,P,C$ in order.Here the complex numbers are, i. $B=-1/2$ , ii. $C=1/2$ and iii. $P=x+iy$
By simplifying the equation obtained in the $4th$ step, we get that $\angle{BPC}={150}^{\circ}$

You may consider this as a solution because I have provided all the steps required.(But this step completely depends on you :P )

$Nice one:$ But Here is a still simpler one :)

Solution to $3rd$ stuff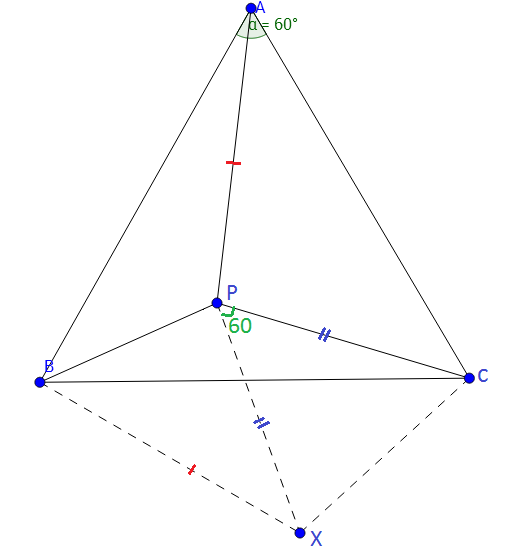 $Construction$ : Draw $PX$ = $PC$ such that $\angle CPX = 60^{\circ}$ . Finally join $BX$ and $CX$ .

Clearly $\Delta CPX$ is equilateral. => $CX$ = $PC$ ------ $1$ and Also, $\angle PCX = \angle ACB$ = $60^{\circ}$ => $\angle PCX - \angle PCB = \angle ACB - \angle PCB$ => $\angle BCX = \angle ACP$ ------- $2$

From the results in $eq^{n}$ $1$ , $2$ and that $BC$ = $AC$ , we conclude that $\Delta BCX \cong \Delta ACP$ . => $BX$ = $PA$

But $Given$ $PB^{2} + PC^{2}$ = $PA^{2}$

=> $PB^{2} + PX^{2}$ = $BX^{2}$ ............... [ $PC$ = $PX$ and $BX = PA$ ]

Therefore by the converse of $Pythagoras... theorem$ , it is obvious that $\angle BPX$ = $90^{\circ}$

Thus the required angle = $\angle BPC$ = $\angle BPX + \angle CPX$ = $90^{\circ}$ + $60^{\circ}$ = $150^{\circ}$ .

Vishwash Kumar ΓΞΩ - 4 years, 2 months ago

1) p = 7

$p(p - 1) = 2(y + x)(y - x)$

comparing of y + x and p gives p = 7

Dev Sharma - 5 years, 8 months ago

Sorry to say , but you have dropped out some cases. This solution is incomplete.

Nihar Mahajan - 5 years, 8 months ago

let me check

p can't divide 2 and y - x so p divides only y + x and by some observations, i found x is equal to or smaller than 2, so when x = 1 then p = 1. No. then x = 2 so p = 7

@Dev Sharma – Include this in your previous comment and complete your solution. Don't make parts of your solution.

@Dev Sharma Kindly always post a full solution.

Mehul Arora - 5 years, 8 months ago

7) @Nihar Mahajan We have $ab(a-c)+bc(b-a)+ca(c-b)$ .

Multiplying we get $a^2b+b^2c+c^2a-3abc= abc(\frac {a}{c}+ \frac {b}{a} + \frac {c}{b}-3$ ).

By AM-GM inequality, $\frac {a}{c}+ \frac {b}{a} + \frac {c}{b} \ge 3$ .

Therefore, minimum value of the expression $\frac {a}{c}+ \frac {b}{a} + \frac {c}{b}$ is $3$ .

Therefore, minimum value of $ab(a-c)+bc(b-a)+ca(c-b)$ is $0$ and equality occurs when $a=b=c=0$ .

@Surya Prakash @Nihar Mahajan @Svatejas Shivakumar There seems to be a blunder in problem statement of Q4). I guess it meant " Simplify $\large \binom{n}{0} + \binom{n}{3} + \binom{n}{6} + \binom{n}{9} + ... \binom{n}{ 3 \cdot \lfloor \frac{n}{3} \rfloor }$ ." The last summand being $\binom{n}{n}$ doesn't make sense at all if $n$ is not a multiple of $3$ .

Venkata Karthik Bandaru - 5 years, 8 months ago

Its correct.

Try substituting $n = 4$ in the summation. The link between last term of the summation ( i.e. last summand ) and previous summands is not clear.

@Venkata Karthik Bandaru – It satisfies.

@Saarthak Marathe – Let $f(n) = \large\binom{n}{0} + \binom{n}{3} + \binom{n}{6} + \binom{n}{9} + ... \binom{n}{n}$ .Then $f(4) = \binom{4}{0} + \binom{4}{3} + \binom{4}{4}$ ? I am certainly sure about the last summand being $\binom{n}{ 3 \cdot \lfloor \frac{n}{3} \rfloor }$ , contrary to $\binom{n}{n}$ mentioned in the question.

@Venkata Karthik Bandaru – In that way!!!!! Then it is understood that it should be $3.[\frac{n}{3}]$

@Saarthak Marathe – I guess it would have been understood if it was just ..... , but rather it mentioned the last summand wrong 😓.

1) Solve $y^3 = x^3 + 8x^2 - 6x + 8$ for positive integer x and y.

2) Two positive integer a and b such that $a^{a}b^{b}$ is divisible by 2000. What is least possible value of ab?

3) Find all real a for which $x^4-2ax^2+x+a^2- a$ has all real root

Hey Nihar plead post solution for question(9). Thanks!

Harsh Shrivastava - 5 years, 6 months ago

$Question 5: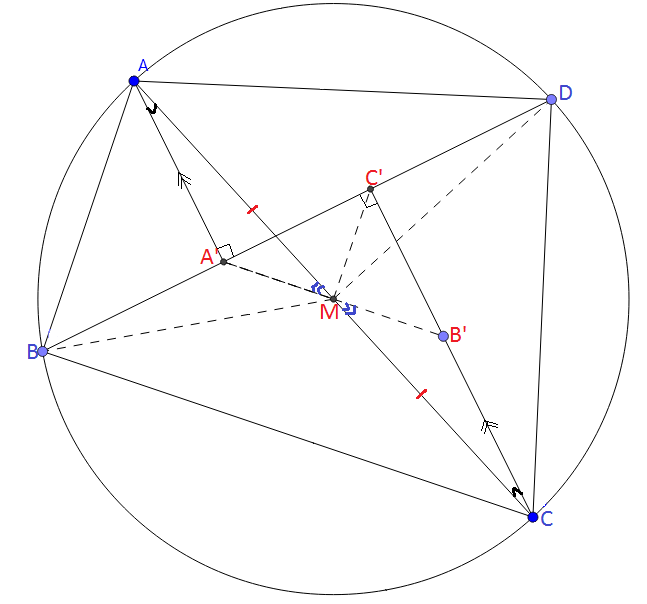$ $Const:$ The constructions are clearly shown in the above $diagram.$ Join $BM$ , $DM$ , $C'M$ ,finally join $A'M$ and produce it to meet $CC'$ at $B'$ .

$AB$ is the diameter of the $\odot ABCD.$

=> $\angle ABC$ = $\angle ADC$ = $90^{\circ}$ => $BM$ = $DM$ [= $1/2AC$ ] => $\angle MBC'$ = $\angle MDC'$ --- $1$

Clearly, $\Delta AA'M \cong \Delta CB'M$ => $A'M$ = $B'M$ => $M$ is the midpoint of $A'B'$ .

But $\Delta A'B'C'$ is right angled at $C'$ and also $M$ is the midpoint of $A'B'.$ => $C'M$ = $A'M$ ---- $2$

=> $\angle MC'B$ = $\angle MDA'$ ----- $3$

From the $eq^{n}$ $1$ , $2$ and $3$ : $\Delta MC'B \cong \Delta MDA'$ => $BC'$ = $A'D.$

$K.I.P.K.I.G.$

Would anyone help me in problem number 10

Rupam Maiti - 8 months, 2 weeks ago

If $x^{5}-x^{3}+x=\eta$ , the minimum value of $x^{6}$ in terms of $\eta$ .

Shivam Jadhav - 5 years, 8 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$