Roots of Unity (and Beyond)

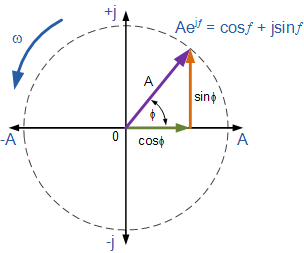
In this note, we will explain the mechanics for solving the roots of a complex number. It begins with a simple argument, then many elegant results follow.

We begin with the complex plane, where the vertical axis represents the imaginary numbers and the horizontal axis represents the real numbers (as pictured above). Normally, we define a complex number as $z = a+bi$, where $a, b$ are real numbers. We can also express the number in polar coordinates: $r = \sqrt{{a}^{2}+{b}^{2}}$ and $\theta = arctan\left( \frac{b}{a} \right).$

(Sorry, engineers like to use phi for angles, and j for imaginary numbers)

If we treat $a$ and $b$ as the components of a vector with magnitude $r$ from the origin, we can represent all imaginary numbers in polar form $z=r\left(cos \theta + isin \theta\right).$

By the well-known Taylor expansions of $cos x$, $sin x$, and ${e}^{x}$, we can easily show that ${e}^{i\theta} =\left(cos \theta + isin \theta\right).$

See proof

By treating this identity from a trigonometric perspective, we discover that ${e}^{i2\pi k} =1$; hence, if we solve for ${z}^{n} =1$, it follows that ${r}^{n}{e}^{in\theta} = {e}^{2\pi ik}.$ This implies that $r=1$ and $\theta = \frac{2\pi k}{n}$ where $k =0,1,2,...,n-1$. Consequently, the roots of unity are $cos\left(\frac{2\pi k}{n}\right)+isin\left(\frac{2\pi k}{n}\right).$

But what do we do to solve the roots of any complex number? Well, we have to make a transformation by finding the ${n}^{th}$ root of $r$ and adding $\frac{2\pi k}{n}$ to the angle value for the particular complex number! To visualize this, we look back at the diagram and notice the following:

1)For $z = 1$, the initial angle $\theta$ is zero. However, for $z=a+ib$ we have $\theta = arctan\left( \frac{b}{a} \right)$.

2)For $z = 1$, the magnitude is one. However, for $z=a+ib$ we have $r = \sqrt{{a}^{2}+{b}^{2}}$.

Hence the roots of a complex number are

${r}^{\frac{1}{n}}\left[cos\left(\theta +\frac{2\pi k}{n}\right)+isin\left(\theta + \frac{2\pi k}{n}\right)\right]$

for $k = 0,1,2,...,n-1$.

Check out my other notes at Proof, Disproof, and Derivation