Rotational Dynamics Problem!
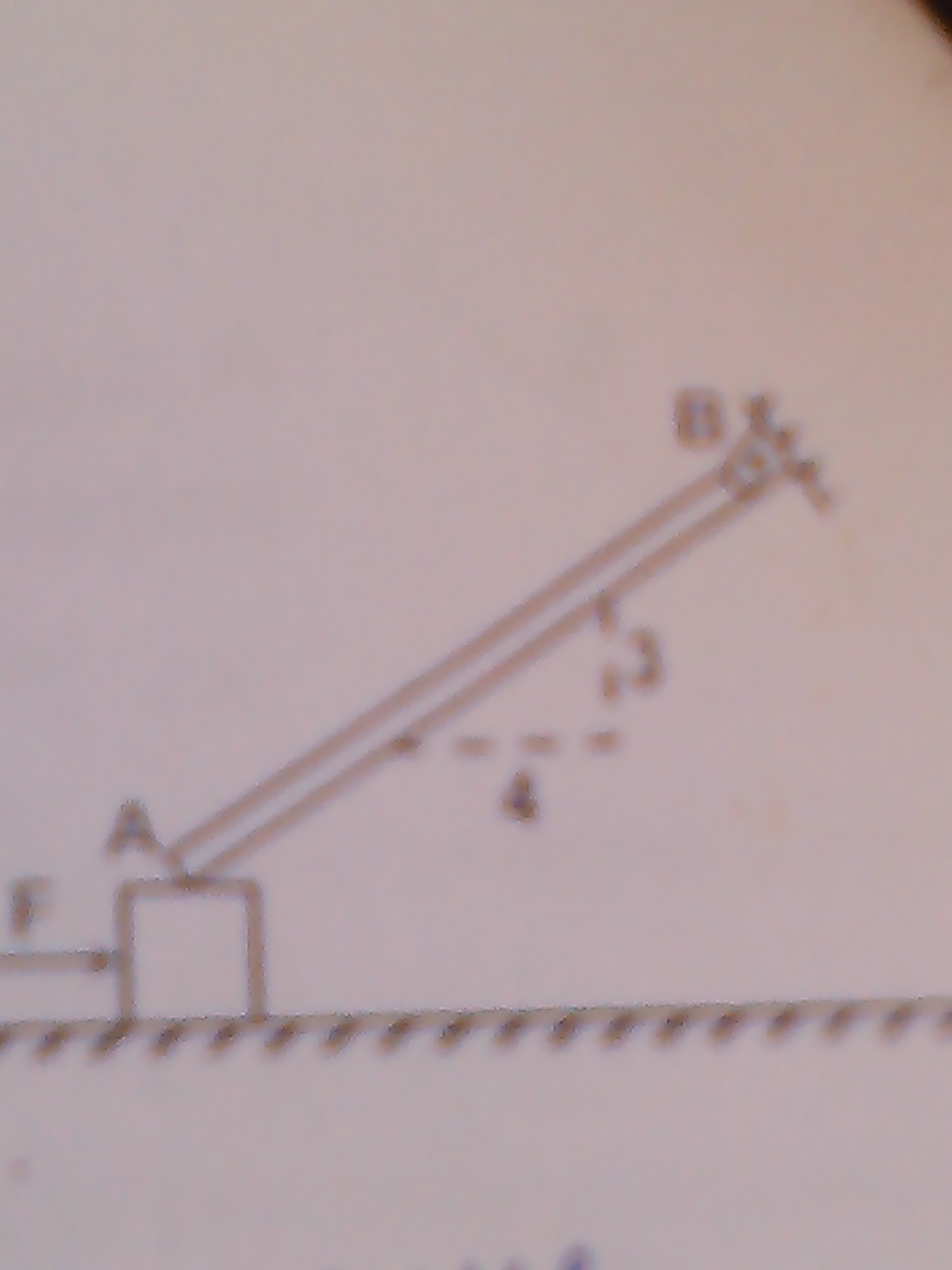
A uniform bar AB 10 m long and weighing 280 N is hinged at B and rests upon a 400 N block as shown. If the coefficient of friction at all contact surfaces is 0.4. The value of horizontal force F required to start the motion of the 400 N block is...?
For a better image(not much better): http://bit.ly/18yUu8D
No vote yet
2 votes
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
272 N .
Log in to reply
I am sorry but the correct answer is 320 N. Could you tell me how you approached the problem???
Log in to reply
Ok i got my mistake , i was not considering torque due to friction on the rod.
Draw proper FBD. Let N1 and N2 be the normal reactions between rod and block and between ground block respectively. Let f1 and f2 be corresponding frictions.
At the verge of slipping , f1=0.4N1,f2=0.4N2
On the rod , we can balance torque apout the hinge.
Anticlockwise torque due to friction and weight = clockwise torque due to normal reaction.
⇒2mglsinθ+0.4N1lcosθ=N1lsinθ ,
⇒N1=200N
Analysing FBD of block ,
N2=Wblock+N1=600N
F≥f1+f2=0.4(N1+N2) = 0.4×800=320N
Log in to reply
Thanks!!! I figured my mistake too. i was not considering torque due to normal reaction.
But when I solved the torque equation, I got N1 as 300N. Can you check why?
Log in to reply
Sorry , i can't check without your equations.
Log in to reply
No sorry never mind, I got it.
A uniform bar AB 10 m long and weighing 280 N is hinged at B and rests upon a 400 N block as shown. If the coefficient of friction at all contact surfaces is 0.4. The value of horizontal force F required to start the motion of the 400 N block is...? what is the solution