Six intersecting cylinders and the Brilliant logo

Six cylinders of unit radius are arranged so that each of their central axes passes through the centres of opposite faces of a dodecahedron. What is the volume common to all six cylinders?

This question, or something similar, was posed by a community member a few months ago. I've enjoyed working on it and meeting several new polyhedra in the process.

The first step in answering this problem is to visualise the shape of the solid formed by this intersection. Solid shapes formed by the intersection of cylinders meeting at a common point are known as Steinmetz solids. It’s almost possible for me to visualise the shape of two cylinders intersecting at right angles. Any more than that becomes very difficult for me. I can readily find pictures on the internet of Steinmetz solids formed by the intersection of two or three cylinders along with formulae for their volumes. I can’t easily find an image for this arrangement of six cylinders though.

Faced with six cylinders, how can we see the resulting solid of intersection? The first thing to note is the symmetry. It’s based on a dodecahedron or, equivalently an icosahedron (the dual solid of the dodecahedron) with the cylinder axes passing through the vertices of the icosahedron.

The Steinmetz solid will have faces that are each portions of a cylinder's surface. Each face is the region of the surface of the cylinder that is closer than any other to the common centre, $O$, of the solid. Each face will be curved rather than flat as they are part of the surface of a cylinder. Lines on this surface parallel to the axis of the cylinder will be straight and parallel to each other following the longitudinal lines of the cylinder’s surface.

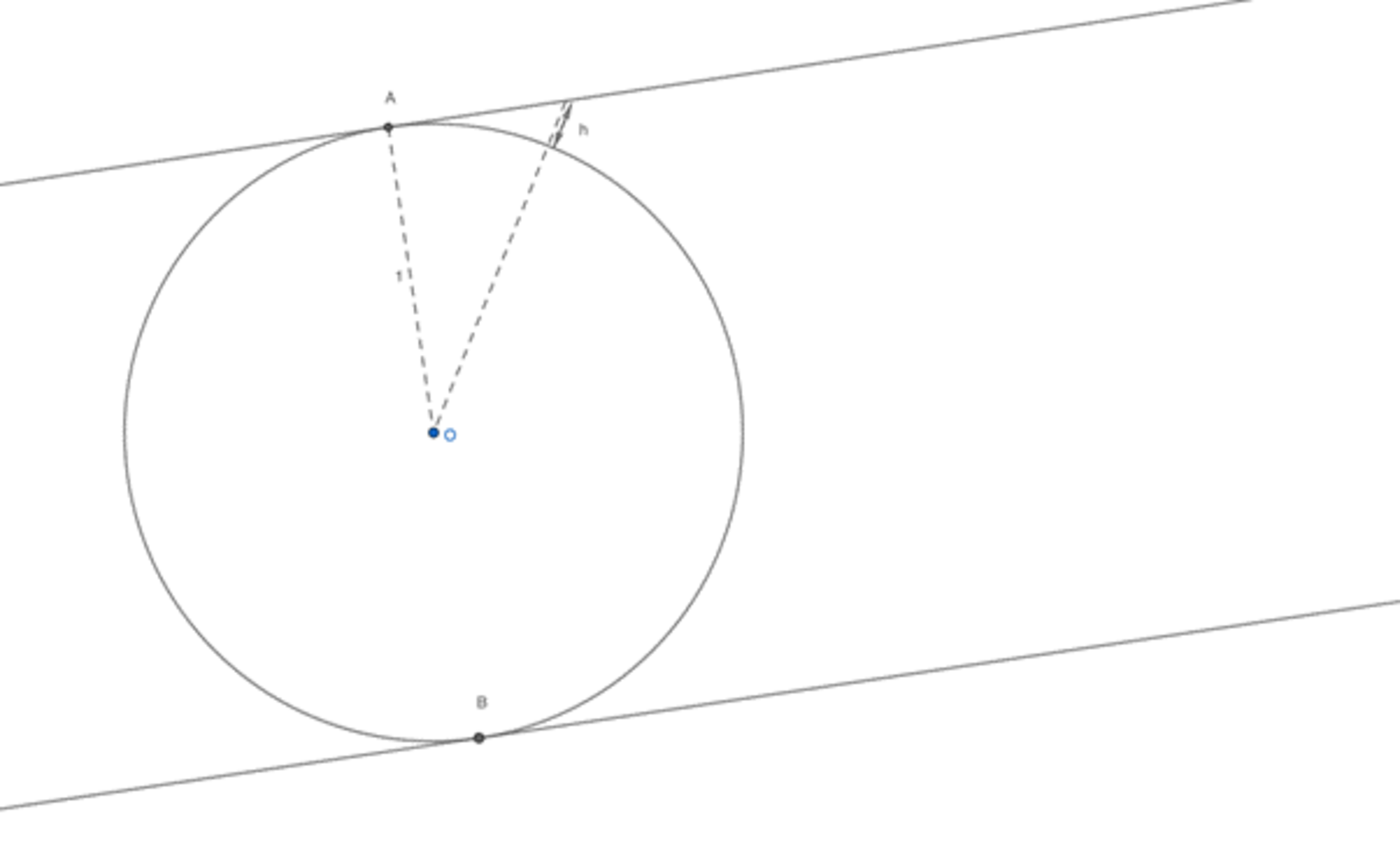
What is the shape of the region(s) on the cylinder surface that are closer to $O$ than any other cylinder? The closest the surface gets to $O$ is 1 unit when a line from the surface to $O$ is perpendicular to the surface. In two dimensions, this corresponds to points A and B in the diagram below. In three dimensions, it corresponds to a great circle around the unit sphere centred on $O$.

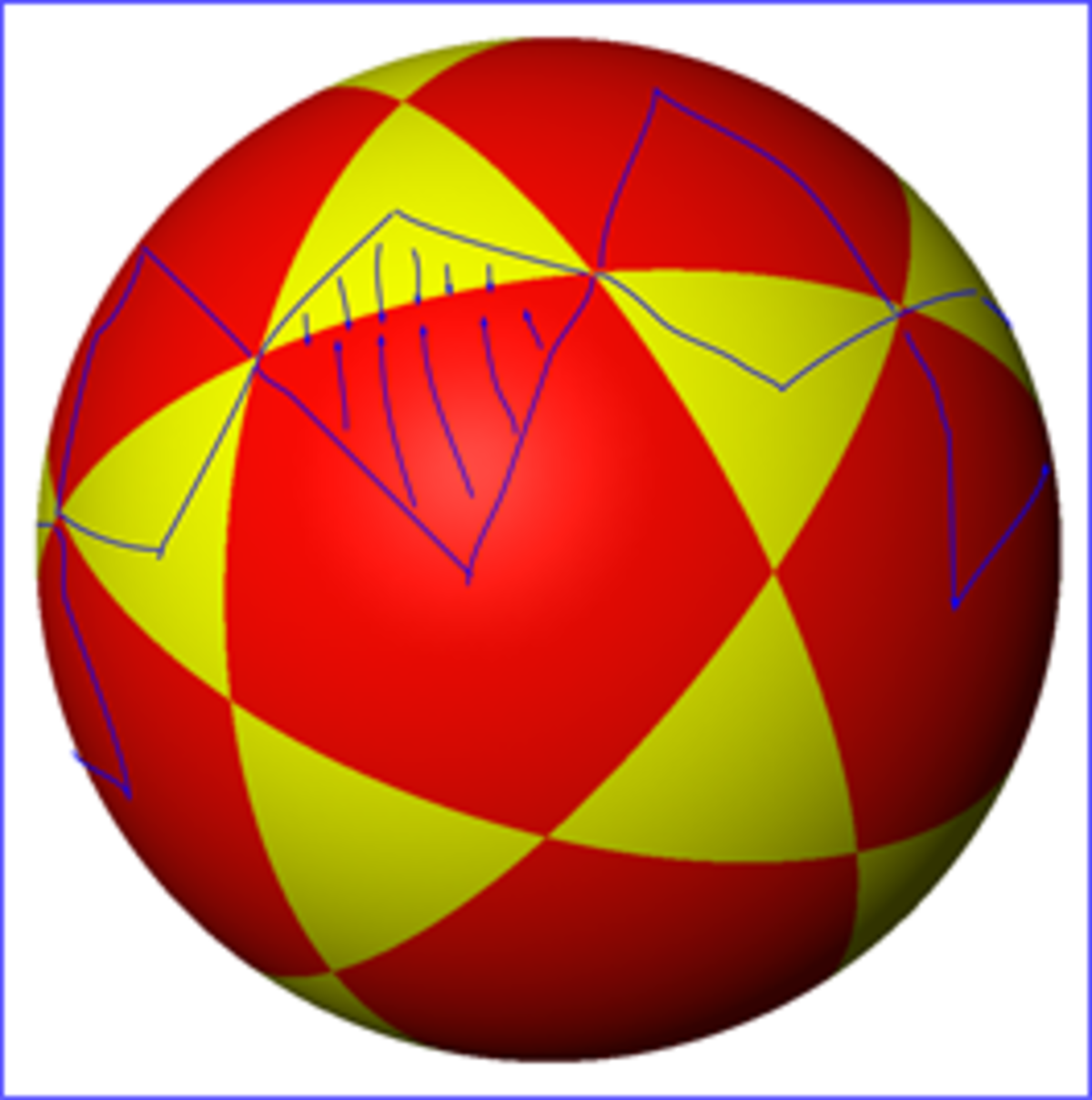
Harnessing the symmetry, we can ask which solid has six great circles and icosahedral symmetry? It’s this thing: a projection of an icosidodecahedron onto a unit sphere. It splits the sphere into triangle and pentagon-like shapes. Each great circle will be on the surface of the final Steinmetz solid.

Any distance away from one of these great circles (either on the sphere or on a cylinder surface) increases the distance between the cylinder surface and $O$ to $1+h$ where $h$ is strictly increasing with increasing distance. (see 2D diagram above). So for any point on the sphere, the cylinder closest to $O$ will be the one that has the closest tangent great circle. Let’s roughly draw these areas near one tangent great circle. Arrows point to the nearest great circle.

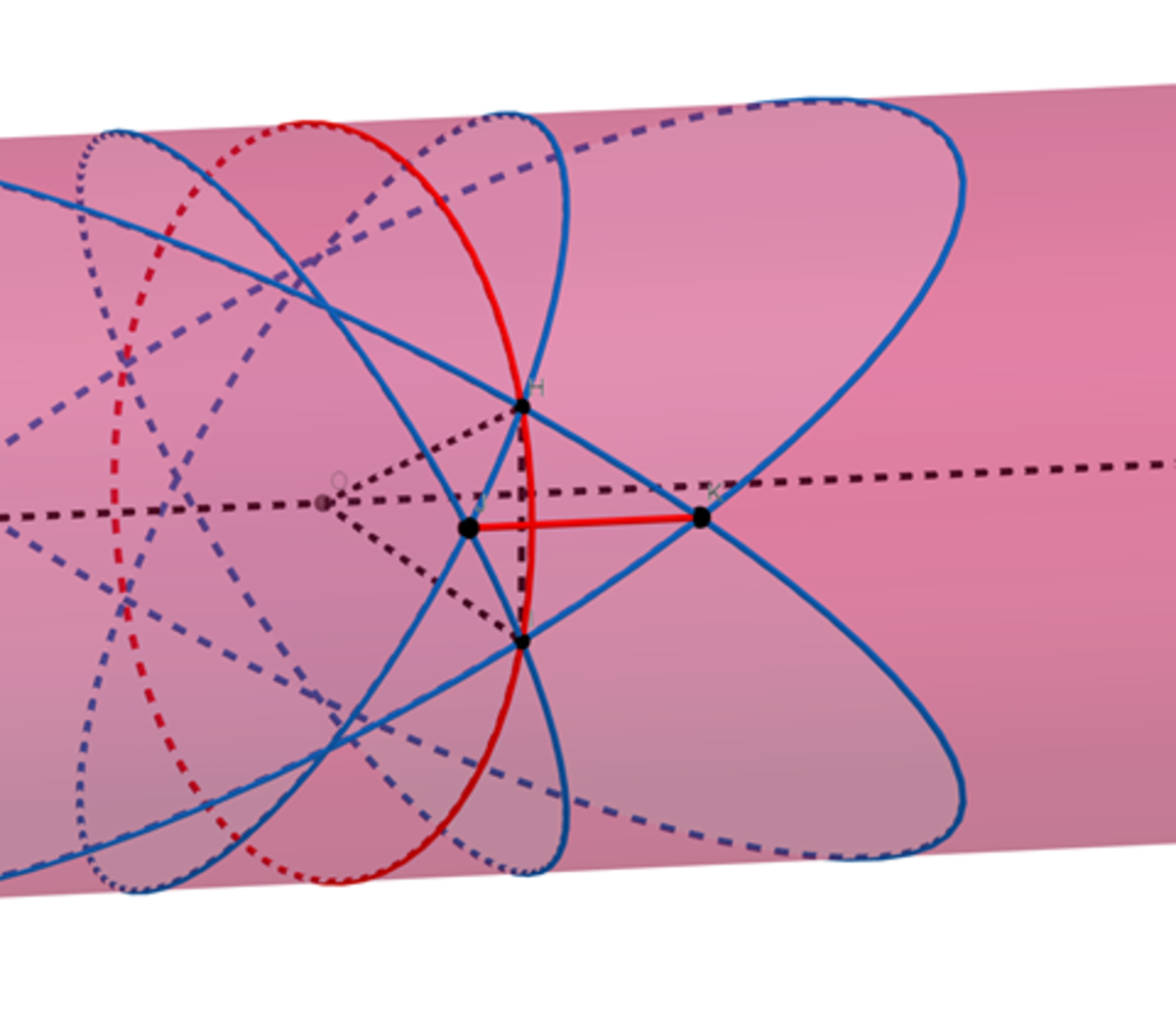
The regions of the cylinder surface we are interested in are roughly kite-shaped and push into adjacent triangle and pentagon-like areas. One diameter, call it $d$, of the kite is an arc of the circle and is curved. The other diameter, $D$, is a longitudinal line on the cylinder and is straight. In the diagram below, the kite-shaped face is formed on the pink cylinder by the four blue ellipses. $D$ runs from J to K while d runs from H to I.

There are ten such faces for each such cylinder alternating in orientation. They encompass the circumference of the tangent great circle. Each face occupies one tenth of the circumference. Six cylinders makes 6 times 10 or 60 faces in total. The resulting solid shape is like a deltoidal hexecontahedron:

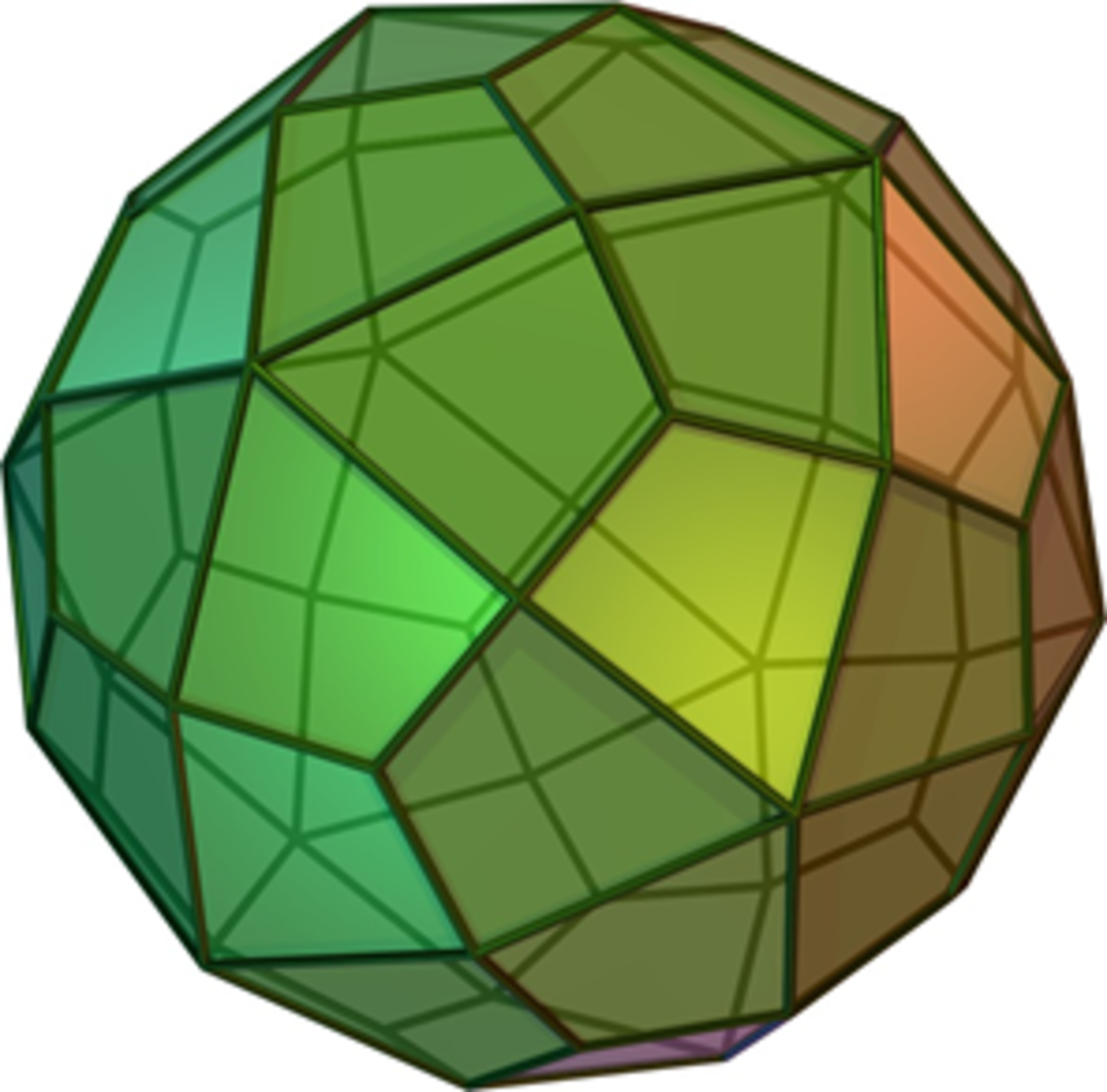
but with curved rather than flat faces, one of which is shown below.

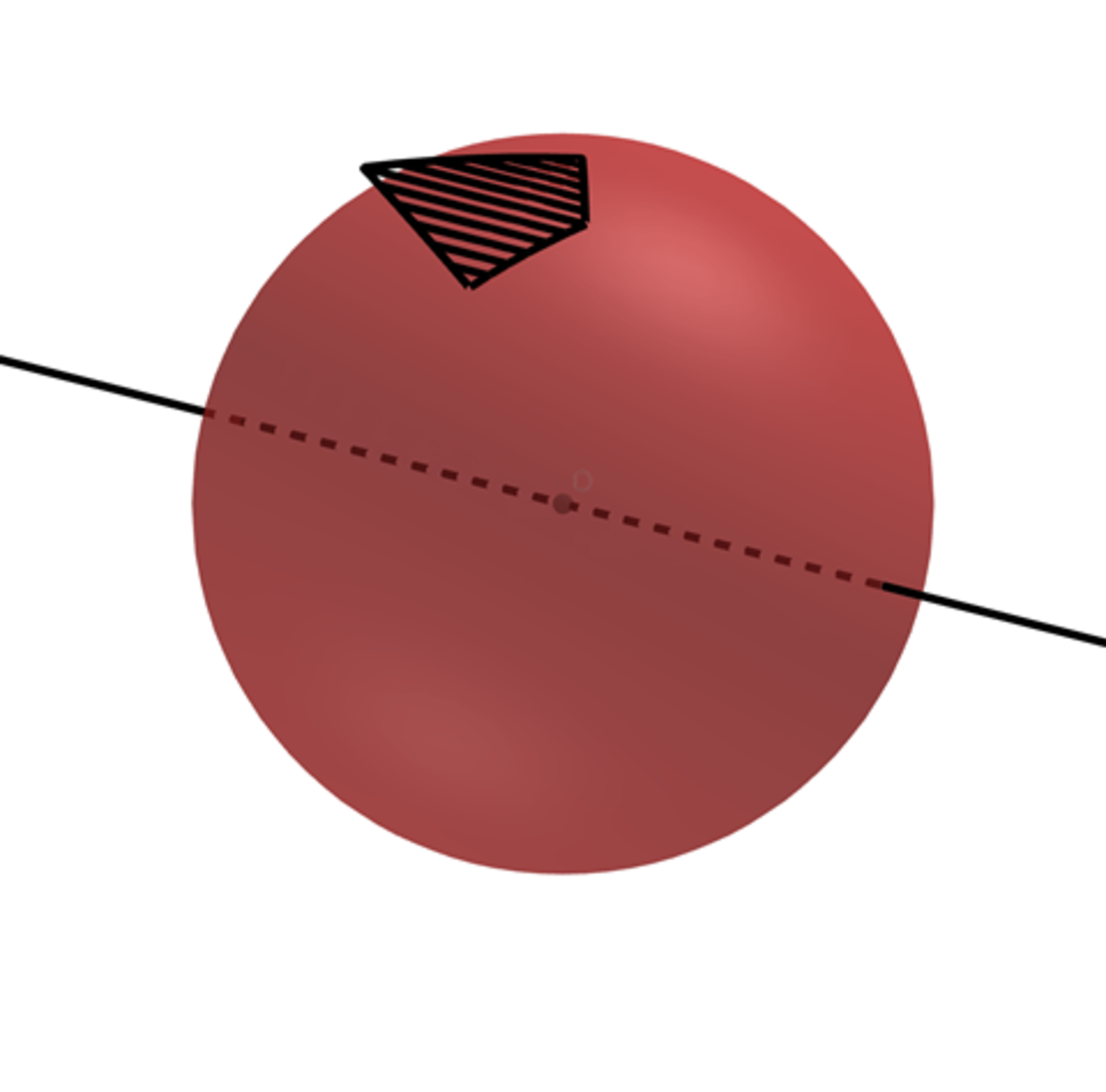
If we add in the straight diagonals, $D$, of each kite shaped face, we get a close approximation of the required Steinmetz solid, a 120-face solid called the disdyakis triacontahedron:

The projection of this shape onto the sphere should be familiar to users of this website:

So that’s an approximation of the shape. What is its volume? If we could work out the volume of the pyramid-like shape with one face as the base and $O$ as the peak, we could multiply by 60 to find the volume. Since the kite-shaped face has an axis of symmetry, we can more easily work out half the volume and multiply by 120.

It’s hard to work with the edges of the face because they are arcs of ellipses. The central diagonal, $D$, of each curved face is however a straight line. Considering only these straight diagonals, $D$, we get yet another polyhedron, a rhombic tricontahedron:

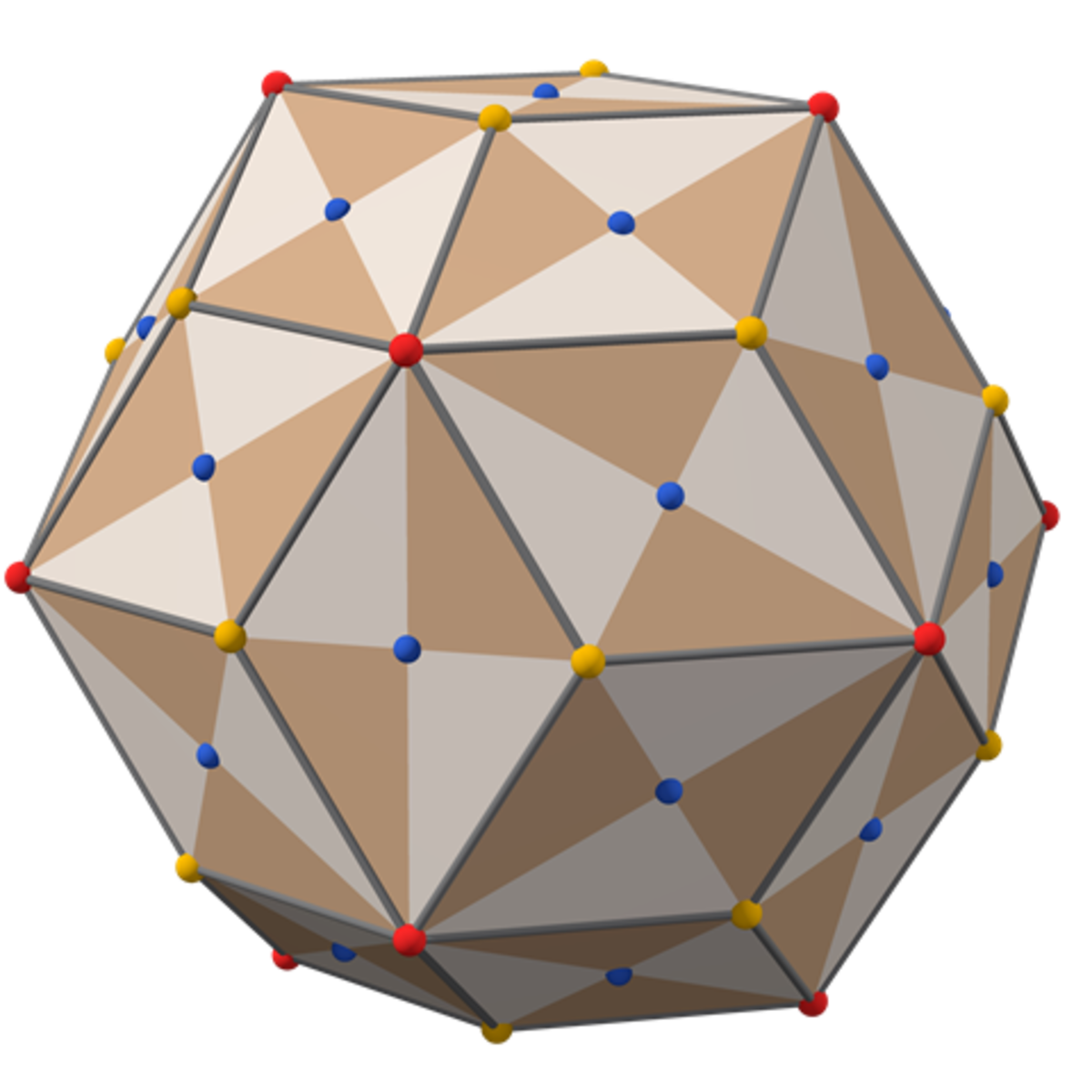
The faces of a rhombic tricontahedron are golden rhombuses; their diagonals are in the golden ratio $\phi$. The parallel lines are separated by a curved arc of length $d = \pi/5$ being one tenth of the circumference of the unit circle. The straight-line distance, $s$, is slightly shorter and is $1/\phi$ being the side length of a decagon inscribed in a unit circle.

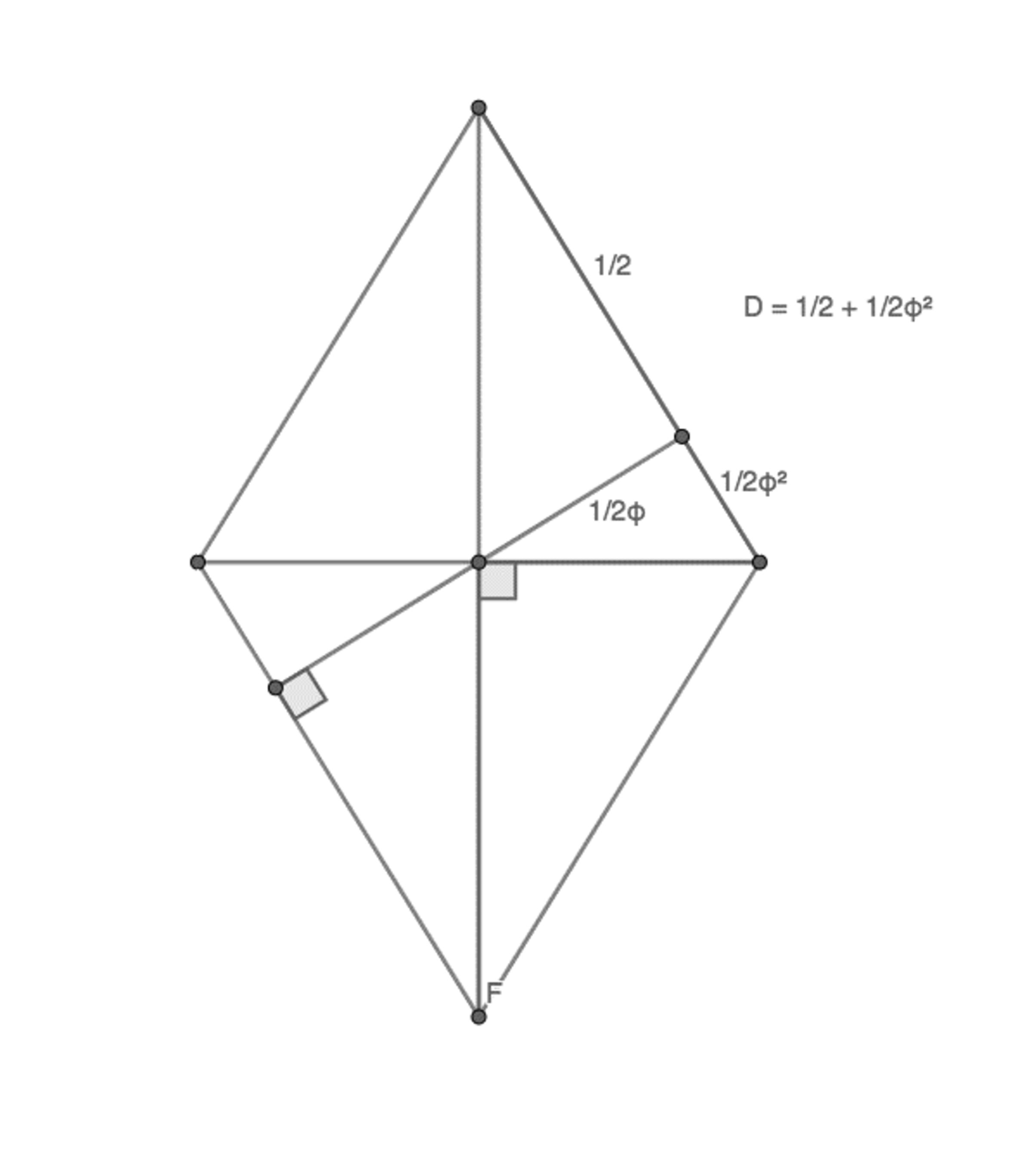
These facts and a little geometry allow us to work out the length of $D$ as $\frac{1}{2} + \frac{1}{2 \phi^2}$ or approximately 0.691 units.

We now have the dimensions we need. Although there are two different triangle shapes making up one half of the kite shape, they have the same area and volume as one triangle with base $D$ and height $d$.

The diagram shows in black the shape and dimensions of this triangular sliver of the whole Steinmetz solid:

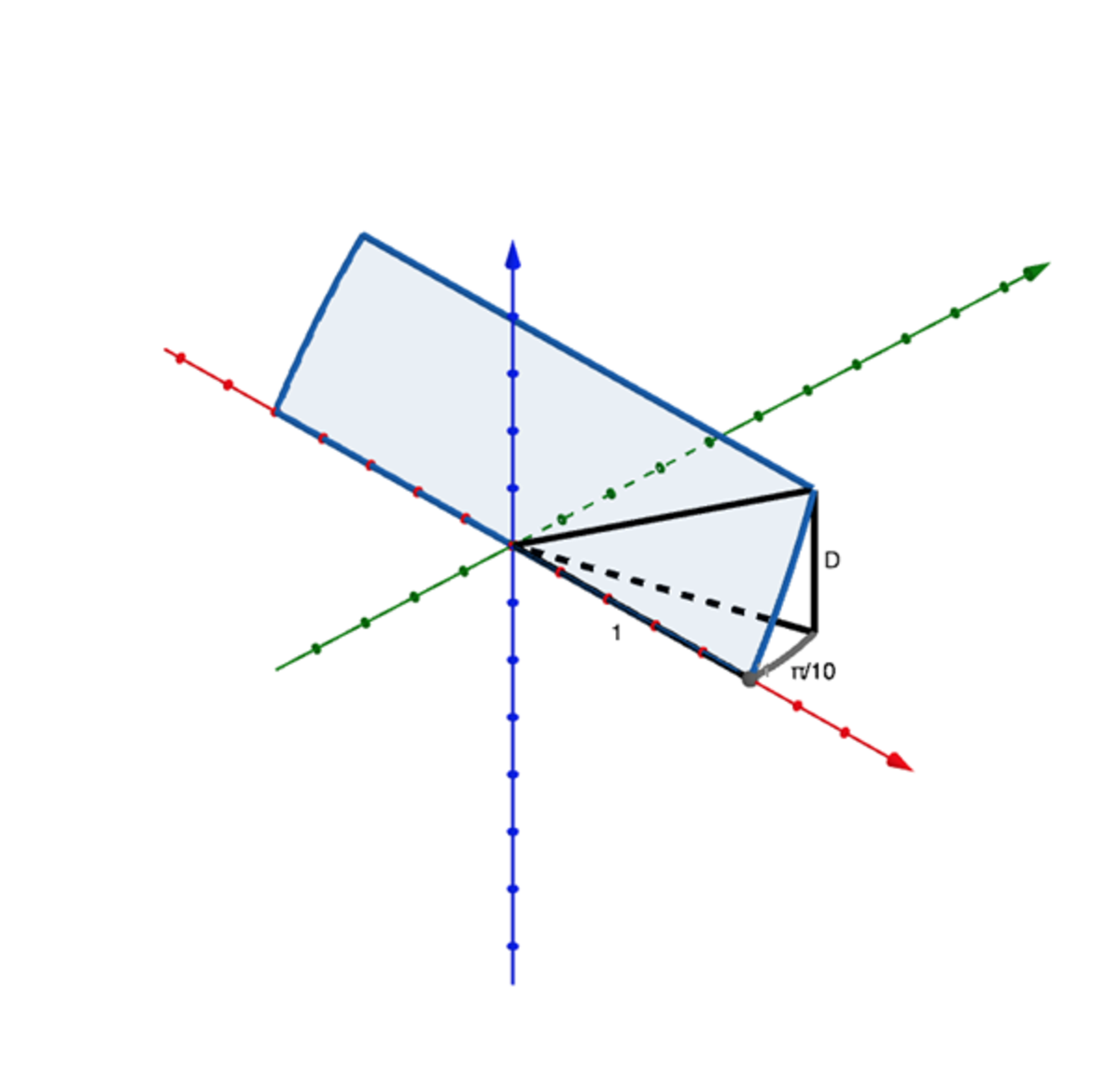
In polar coordinates, the volume of this shape is:

$\int_{0}^{1}\int_{0}^{\pi/10} (height function)\ r\ dr\ d\theta$

where the height function is $y$ multiplied by the slope of the blue plane, $D/\frac{s}{2}\ =\ 2\ \phi\ D$ so the height function in polar coordinates is:

$2\ \phi\ D\ r\ \sin \theta$

Taking the constant out of the integral gives:

$2\ \phi\ D\int_{0}^{1}\int_{0}^{\pi/10} r\ \sin\theta\ r\ dr\ d\theta$

$=2\ \phi\ D\int_{0}^{1} r^2\ \left [-\cos\theta\right ]^{\pi/10}_{0} dr$

$=2\ \phi\ D\ S\int_{0}^{1} r^2\ dr$ , where $S= 1-\cos (\pi/10)$ is the sagitta of a decagon in a unit circle, approximately 0.049

$=2\ \phi\ D\ S\left [\frac{r^3}{3} \right ]^{1}_{0}$

$=2\ \phi\ D\ S\ \frac{r^3}{3}$

It’s interesting to see that this volume scales with the cube of the radius of the cylinders, as expected and follows the pattern of the volume of a pyramid or cone where $V= 1/3 (area\ of\ base)\ times\ height$

Here $r=1$ so $V= \frac{2\ \phi\ D\ S}{3}$ and total volume $= 120\ V = 80\ \phi\ D\ S$. This is 4.378 cubic units, a little more than 4.189 cubic units, the volume of the unit sphere, as expected.

This exploration can be extended in different ways. What is the common volume of intersecting cylinders that are face, edge or vertex-centered with respect to a cube, an octahedron or some other shape? What other pyramids with curved bases have volume as 1/3 base times height? Is there a simpler expression for the volume? I’m interested in your comments.