I LOVE THE DREAM SMP!
There are many ways to look at this problem. Three good ways would be:

1. Directly calculate if you know the formula for frustum volume.

The formula for frustum volume, given bottom radius $R$, top radius $r$ and height $h$, is $V=\frac{1}{3}\pi h(R^2+r^2+Rr).$ Therefore we can plug in $\pi\approx \frac{22}{7}, ~~h=70,~~R=40,~~r=70$ to find the volume (must be converted to Liters): $V=\frac{1}{3}\times \frac{22}{7}\times 70(40^2+70^2+40\times 70=682000 (\text{cm}^3)=\color{#D61F06}682 \text{L}.$

2. Calculate difference of cones not knowing the formula for frustum volume.

Extending the cone by imagination and using similarity, we get the pic below: 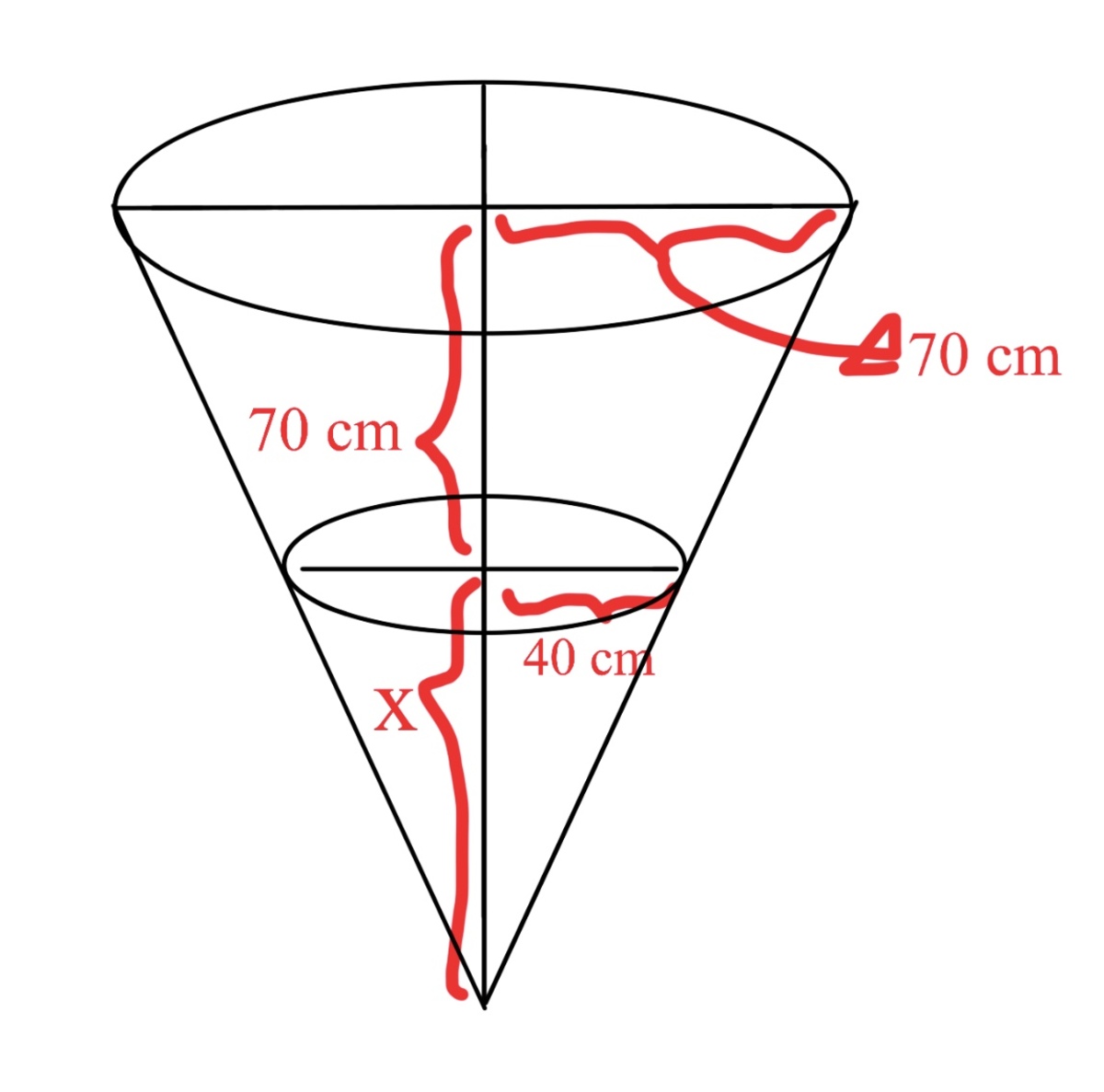Let the height of the increased cone be $x$. By similarity, we get $\frac{40}{x}=\frac{70}{70+x}$. Solve this to get $x=\frac{280}{3}$.
So the volume of the frustum is the volume of the larger cone minus the volume of the smaller cone (the formula for cone volume is $\frac{1}{3}\pi r^2h$ where $r$ stands for bottom radius and $h$ stands for height): $V_{\text{frustum}}=V_{\text{big cone}}-V_{\text{small cone}}=\frac{1}{3}\pi \times 70^2\times (70+\frac{280}{3})-\frac{1}{3}\pi \times 40^2\times \dfrac{280}{3}=682000(\text{cm}^3)~~~\color{#D61F06}\pi~\text{is replaced with}~\frac{1}{3}~\text{here}$

3. Use the ‘Baumkuchen’ integral.

$\scriptsize \color{#D61F06} \text{If under 18, do NOT do at home without adult supervision to avoid brain explosion.}$
This is mentioned in a book I read which finds volumes of 3D-shapes created by rotating the shape bounded by functions $f(x)$ and $g(x)$ in region $a\le x\le b$: $V=2\pi \int_a^b|x||f(x)-g(x)| dx.$ The absolute value brackets are there to make sure $V$ is positive. THIS WORKS ONLY IF THE ROTATED BOUND IS ON THE SAME SIDE OF THE Y-AXIS.
Why is it called Baumkuchen?
It is because Baumkuchen is ‘log-like dessert’ in German, and the integral is like one!
Baumkuchen has log-like stripes Explanation:
We can split the integral into rings formed by the original bound split and rotated around the y-axis individually. 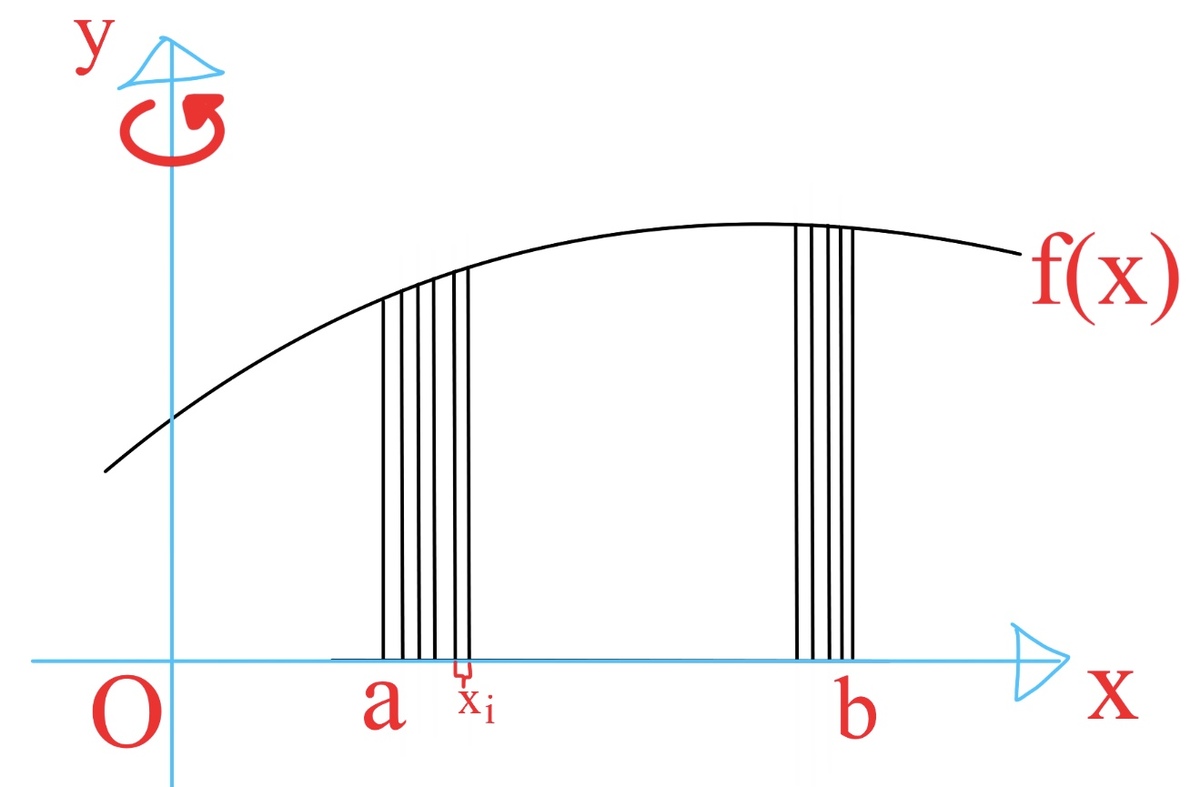Here I made a little mistake when labelling :P $x_i$ should be replaced with $dx$ :)
For simplicity, here I let $g(x)=0$. Of course this can be generalised to other functions as well, given above.
If we cut a single ‘ring’ open, we get its volume by seeing it as a cuboid: 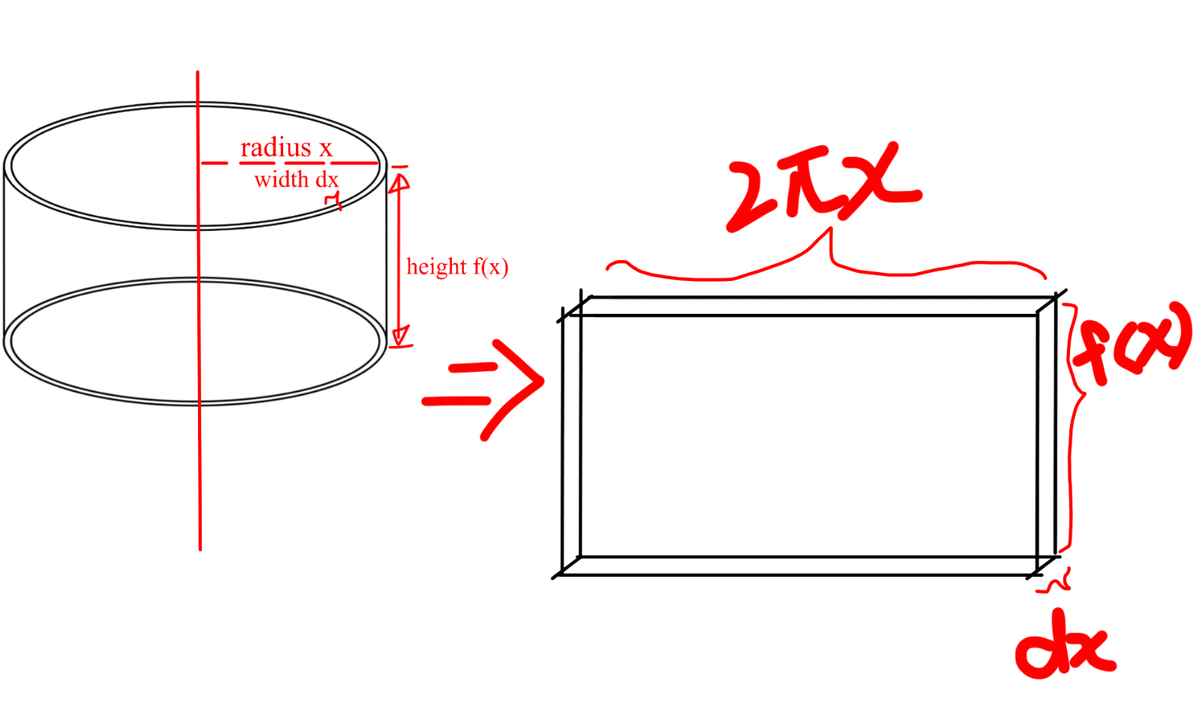I forgot the absolute value brackets :P Enlarge to see clearer :)
Here the volume of the cuboid is $2\pi |x||f(x)|$ because $g(x)=0$ and the $-g(x)$ term is therefore neglected. Summing infinite cuboids gives $V=2\pi \int_a^b|x||f(x)-g(x)| dx.$ So we can see the frustum as a cone chopped off from another as in example 2. This way, the volume of the big cone is the integral with $a=0,b=70$, $f(x)=70$ and $g(x)=\frac{7}{3}x-\frac{280}{3}$. Plug in these to get $V_1=2\pi\int_0^{70} |x||70-(\frac73x-\frac{280}{3})=2\pi \int_0^{70} \frac{490}{3}x-\frac{7}{3}x^2\approx 2\times\frac{22}{7}(\left. \frac{245}{3}x^2-\frac79x^3\right|_0^{70})=75460009.$ Similarly we can apply the same to the small cone to get $V_2=\frac{1894000}{9}$. $V_1-V_2=628000.$ Convert to liters: $628$.