Solve this physics problem

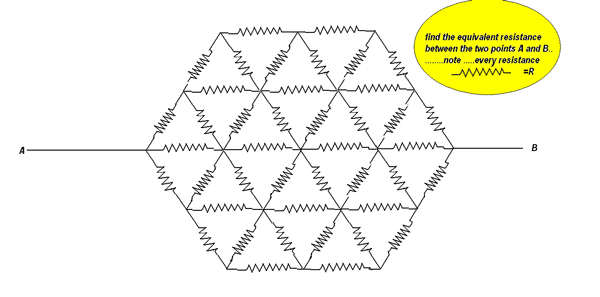
Thanks to all who join this discussion and make it a success....Anyone willing to solve the problem is welcomed. Enjoy it ...!!

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

The correct answer is $\frac{299R}{330} \approx .906R$ .

Using Pranav A.'s method of folding the circuit, and then applying a Delta-Y transformation (http://en.wikipedia.org/wiki/Y-%CE%94transform), I was able to reduce the circuit to a 13-resistor,10-node circuit(https://i.imgur.com/OQ0t9f8.png). From there, you can use the Node-Voltage method (http://en.wikipedia.org/wiki/Nodalanalysis), along with assuming a test voltage applied across A and B, to solve the circuit, although it requires using a rather large system of equations. If anyone knows of a way to further reduce the circuit from the 13-resistor state so that you don't have to get such a large system please tell me.

Ricky Escobar - 8 years, 1 month ago

I too had the same problem. I had to apply the Y-delta transform again and again but it wasn't ending up with nice values so I gave up.

Pranav Arora - 8 years, 1 month ago

IF ANYONE OF YOU FIND THIS PROBLEM IN A BOOK,DON'T THINK I HAVE COPIED IT....I CREATED IT MYSELF....

Sayan Chaudhuri - 8 years, 1 month ago

Do you know the answer?

Sreehari Vp - 8 years, 1 month ago

no, sorry i don't know it..but if anyone describes me how to approach, i could understand....

Sayan Chaudhuri - 8 years, 1 month ago

Thanks Ricky E. !! ... You've been brilliant.

Sung Moo Hong - 8 years, 1 month ago

Is that a pun on the word brilliant? lol! :P

Shourya Pandey - 8 years, 1 month ago

I am not sure about it but first step is obviously folding the circuit about AB. This step retains only the half portion of circuit with all the resistors equal to R/2 except the middle line of four resistors which still have R resistance. The second step involves removing "fake" nodes but I still need to figure out those nodes.

Pranav Arora - 8 years, 1 month ago

there is a great theory to compute the equivalent resistance of such big complicated circuits of resistance....it opines that if any system of resistance is symmetrical about its two opposite point here the two points "A" and "B" then all the points equidistant from this two terminal would be at same potential ......i knew this fact or theorem but i don't know how to apply it here.......i think it would have to be applied here.....try it....

Sayan Chaudhuri - 8 years, 1 month ago

Very complicated......

Sreehari Vp - 8 years, 1 month ago

What are the values of the resistors...are they all same or different

Mukesh G - 8 years, 1 month ago

you have not seen the whole problem..... i have written it in the right corner........ however, each and every resistor have equivalent resistance=R.......

Sayan Chaudhuri - 8 years, 1 month ago

Image Link I simulated this problem. these resistors have 21/19R ohms. I think It is hard to solve by hand.

Sung Moo Hong - 8 years, 1 month ago

Turns out to be 'R' (I think so)

Kashyap Mahler - 8 years, 1 month ago

well really...... current had to do lot of hard work!!!!! please clearly mention your problem, the question is not clearly visible.

DIKSHA VERMA - 8 years, 1 month ago

Delta Y transformation is the only way(known to me), and you will definitely need a good calculator!!

Shourya Pandey - 8 years, 1 month ago

first we change the delta connection into star connection and now we solve it easy series and parallal combination

Attain k Gupta - 8 years, 1 month ago

would you please elaborate it....?...i'm unaware of these connections.....

Sayan Chaudhuri - 8 years, 1 month ago

http://en.wikipedia.org/wiki/Y-%CE%94_transform

Ricky Escobar - 8 years, 1 month ago

Consider each resistor 'R' Fold the circuit along AB. When resistors overlap, consider it a parallel combination and replace it by 'R/2'.

So, except the 4 resistors in the AB line, you get half the circuit where each resistor is 'R/2'. Now, draw a line of symmetry along the perpendicular bisector of AB. There are two nodes on this line, the mid point of AB and the midpoint of the bottom line. Remove these connections as follows : for the top:

something like --------- ^

and for the bottom, something like : v

Now use the normal laws and solve the problem.

Kashyap Mahler - 8 years, 1 month ago

What's your answer??

Kaustubh Olpadkar - 7 years, 10 months ago

I think the answer is 52R/45.

Rafael Saboya - 8 years, 1 month ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$