Solve this!
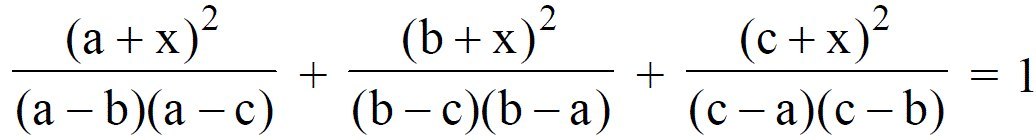
Look Closely...it's a quadratic equation. Now find the number of solutions it has.
No vote yet
3 votes
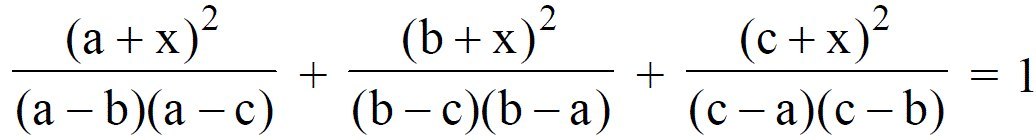
Look Closely...it's a quadratic equation. Now find the number of solutions it has.
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
take L.H.S=f(x), and it is easy to show that f'(x)=0; for all x. ie, f(x)= k = f(-a)= 1, so for all x f(x)=1;
Log in to reply
That is a good observation. A simpler approach would be to make common denominator and consider the quadratic polynomial in x, and easily see that the quadratic coefficient and linear coefficient are both 0.
If the L.H.S=f(x) (if none of the a,b,c's are equal to each other) then f(x)=1 for all x in R. So f(x)-1=0 for all x in R. Thus f(x)-1=p(x) is the zero polynomial and not a quadratic.
its, not a quadratic equation as such because it has 3 real roots
Log in to reply
yah! u r right its an identity............ just for confusion.
yes, my answer of -a, -b, -c is not correct as indeed it is an identity function the equation is satisfied for all x belonging to R.
the roots are -a,-b,-c, assuming a, b, c are distinct real numbers
Log in to reply
how did you got the answer? plzzz explain....i'm not able to solve! :|
Log in to reply
You got 1 on both sides?
Log in to reply
i am not getting a clear solution
Log in to reply
Because if you take lcm of the denominators and expand, and do some algebra there is no x left, infact u get 1=1
Log in to reply
arey.....i took the denominator on the r.h.s. and got 0=0
but m wondering how to get solutions......
this equation is forming an identity i guess
Log in to reply
1=1 implies 1-1=0 so 0=0 :P right?
Log in to reply
very funny.......ha! :/
yes
Log in to reply
can u write the solution plsss....
I wonder. Did you get this from Praveen Tyagi's FB profile?
Log in to reply
??
Log in to reply
Look, you just liked my comment. lol