Speeding up the calculation of $\zeta(2)$ .

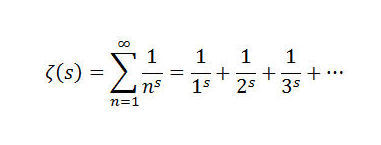
A year ago, I have posted this article, it states that if you want the correct result close by $0.01$ you should calculate about 100 terms which is huge by hand (Euler hadn't W|A to help him at the time he Calculated it ).

A way to speed up the convergence is to use $\zeta(2)=2\sum_{n>0} \frac{(-1)^{n+1}}{n^2}$ , our goal is to see how much is it faster. We set : $a_m= \sum_{n=1}^{m} \frac{1}{n^2} \ \ \ \ \ , \ \ \ \ \ b_m=2\sum_{n=1}^{m} \frac{(-1)^{n+1}}{n^2}\ \ \ \ \ , m>1$

Prove or disprove that : $n \left|\frac{\zeta(2) -b_n}{\zeta(2) - a_n} \right|\to 1$ This means that $(b_n)$ converge a lot quicker than $(a_n)$ .

Image credit : Recovering Lutheran blog .

#Calculus #RiemannZetaFunction #Convergence #SummationOfSeries

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Are there any established series that converge faster than $(bn)$ ?

حكيم الفيلسوف الضائع - 6 years, 11 months ago

Yes of course, check this page.

Euler did not know all these fancy series (but the first) but he managed to get $20$ decimals using the Euler-Maclaurin summation formula which is also better than $b_n$ .

Haroun Meghaichi - 6 years, 10 months ago

Alright thanks!

حكيم الفيلسوف الضائع - 6 years, 10 months ago

@Pratik Shastri @Ronak Agarwal @Kishlaya Jaiswal @Azhaghu Roopesh M

U Z - 6 years, 3 months ago

@Pranav Arora ,@Michael Lee ,@Tunk-Fey Ariawan, @Michael Mendrin (and all calculus guys). What do you think of this problem ? I can post hints if you want.

Another thing, what kind of calculus problems do prefer ? AFAIS, it is integration.

Haroun Meghaichi - 6 years, 10 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Speeding up the calculation of ζ(2)\zeta(2)ζ(2).

Comments

Speeding up the calculation of $\zeta(2)$ .