Spring Potential Energy Problem

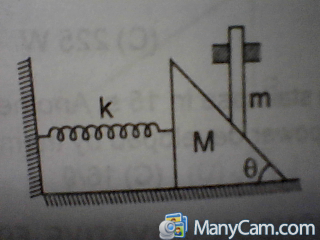
A wedge of mass M fitted with a spring of stiffness 'k' is kept on a smooth horizontal surface. A rod of mass m is kept on the wedge as shown in the figure. System is in equilibrium. Assuming that all surfaces are smooth, the potential energy stored on the spring is:

A) $\frac{mg^2tan^2\theta}{2k}$ B) $\frac{m^2gtan^2\theta}{2k}$ C) $\frac{m^2g^2tan^2\theta}{2k}$ D) $\frac{m^2g^2tan^2\theta}{k}$

#Physics

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Make free body diagram of forces on both the blocks one by one. For wedge of mass M the forces acting along the floor are N sinθ (normal reaction from block of mass m) and kx. Next, make free body diagram of block of mass m. Forces acting on it perpendicular to the floor are N cosθ and mg. Solving these equations

Nsinθ = kx,

Ncosθ = mg,

We get the value of x, hence value of potential energy can be evaluated.

Lokesh Sharma - 8 years, 1 month ago

vijay sakhamudi - 8 years, 1 month ago

Solution????

Shubham Srivastava - 8 years, 1 month ago

Start with determining the state of spring at equilibrium. Should it be compressed or stretched to keep the system at equilibrium?

Pranav Arora - 8 years, 1 month ago

My attitude towards the problem is this: The weight, mg, of the rod will have 2 components- mgsin0 and mgcos0. The component, mgcos0, can be again resolved into two vectors having a horizontal component, mgcos0sin0. For equilibrium, the spring force should be equal to horizontal force. Therefore, mgcos0sin0= kx. We can now substitute value of x from this equation in the equation for spring potential energy, i.e., 0.5kx^2.

Shubham Srivastava - 8 years, 1 month ago

I fear your reasoning is not accurate. You are making components of components. This is probably wrong way and you will get the wrong answer I think.

Lokesh Sharma - 8 years, 1 month ago

mgcos0 (0 to be read as theta) is not a component but the normal reaction of m on M... So there are two forces on M....one is the spring force kx which is horizontal and towards right...and the other is the normal reaction of m on M which towards left, and downwards making an angle of (ninty - theta) with the horizontal...So, on resolving mgcos0 in the horizontal left direction, we get mgcos0sin0...and for M to remain in equillibrium, kx should be equal to mgcos0sin0...

so,

mgcos0sin0 = kx

x=(mgcos0sin0)/k

the potential energy stored in spring = 1/2(k . x^2)..

solvong further will give the answer... So the explanation of Shubham S is accurate....

SAMARTH M.O. - 8 years ago

kx=mgtan@

x=mgtan@/2k

1/2 kx^2 = m^2g^2tan^2/2k

ANONYMOUS . - 3 years, 2 months ago

BY DIMENSIONAL ANALYSIS IT CAN ONLY BE C OR D MOSTLY C

Vasanth Balakrishnan - 8 years, 1 month ago

Mind keeping Caps Lock off. :P

Pranav Arora - 8 years, 1 month ago

how can u say it is mostly c)?

suresh muthuraman - 8 years, 1 month ago

make forces acting on M, weight of m & a force F which is acts opposite to spring force to keep system is in equilibrium. then \Tan\theta\ = F\mg. from this find out F and substituted in P.E = F*2\ 2K get the ans... (C) is correct

Srinivas Santoshi - 8 years, 1 month ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$