Straightedge and compass constructions

This is a quick note about straightedge and compass constructions, in relation to my set.

A quick definition: a straightedge is an arbitrarily long straight edge, and a compass is a circle drawing tool. Specifically, with a straight edge you can:

  • Pick any two lines and draw the line through them

  • Pick a point and draw a line through it

  • Draw an arbitrary line

And with a compass you can:

  • Pick two points, A,BA,B and draw a circle centered at AA with radius ∣AB∣|AB|

  • Pick a point and draw a circle centered at that point

  • Draw an arbitrary circle going through a point

  • Draw an arbitrary circle

Just a quick note about a compass, assume in the questions that you are using a non-collapsing compass, that is, if you draw a circle then you can make your next circle have the same radius as the circle you constructed free of charge.

I'll call a geometric construction constructible if it can be constructed with a straightedge and compass. For example

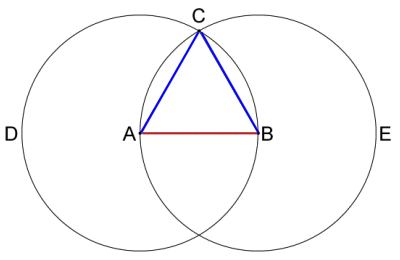
which shows that an equilateral triangle is constructible.

A constructible number, say xx, is defined as follows:

If given a unit length, it is possible to construct a segment of length xx.

Also a shape is constructible given another shape if it is possible to construct another shape given the first one. So although a 2222-gon is not constructible, it is constructible given an 1111-gon.

Lastly a use is a single use of a compass or straightedge, as defined above. So the equilateral triangle takes 5 moves.

Again this is in relation to my set.

#Geometry

Note by Wen Z
4 years, 9 months ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

There are no comments in this discussion.

×

Problem Loading...

Note Loading...

Set Loading...