Stubborn Rectangle
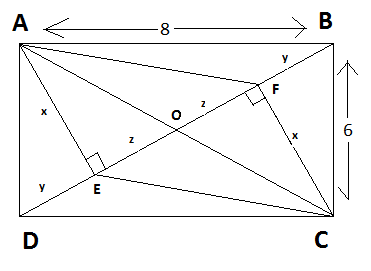
ABCD is a rectengle.\(AE \perp BD\) and \(CF \perp BD\).Let AE=x unit,ED=BF=y unit and OE=OF=z unit.AB=\(8\) unit;BC=\(6\) unit.What is the value of \(\left \lfloor (x+y+z)^2 \right \rfloor\)
No vote yet
1 vote
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
Well this problem looks simple First we see by Pythagoras theorem in triangle ADB that BD=10 So We conclude that y+z=10/2=5 Now area of triangle ADB is 24 So 24=21×BD×AE i.e.24=21×10×AE i.e. AE=1048 So we get what we desire
The diagonals of a rectangle bisect each other. Furthermore, by Pythagorean's theorem, AC=10, so AO=DO=5. Using these same results, we get
y+z=5
x2+z2=25
x2+y2=36
Subtracting the last two equations we get y2−z2=11, so (y−z)(y+z)=11. Substituting the first equation, we get y−z=511. Doing a linear combination with y+z=5 we get 2y=536 so y=518 and z=57. Using one of the equations to find x we get that (x+y+z)2=(549)2=252401, and the greatest integer less than or equal to that is 96.
Motivations in this problem: Nothing really too fancy, just finding what we're given using pythagorean's theorem (which should be obvious given the right angles and side lengths of 6 and 8) and then solving a system of equations.
Log in to reply
Wow nice approach. Thanks for one more method.
(24/5 + 5)^2
I thnk answer is 96.04 In triangle ABC = AB^2 + BC^2 = AC^2 64 + 36 = 100 AC = 10 AC = BD = 10 then 2(y+z) = 10 y+z = 5 z = 5-y (1) AD = BC= 6 then AD^2 = DE2 + AE2 36 = X2 + Y2 (2) In Triangle AOE and COF OE = OF ANGLE AEO = ANGLE CFO ANGLE AOE = ANGLE COF TRIANGLE AOE CONGRUENT TO TRIANGLE COF THEN AO = OC so AC= 10 then AO = 5 Also In Triangle AOE AO2 = AE2+OE2 25 = x2 + z2 (3) 25 = x2 + (y-5)2 25 = x2 + y2 + 25 - 10y 0 = x2+y2 - 10y(4) subtracting 4 from 2 we get 10y = 36 y = 3.6 from (1) we get z = 1.4 putting value of z in 3rd equation we get 25 = x2 + 1.96 x2 = 23.04 x = 4.8 x+y+z = 1.4+3.6+4.8 = 9.8 (x+y+z)2 = (9.8)2 = 96 .04
Ans is 96.04
96.04
(9.8)^2 means 96.04 is the answer.
96.04
answer is 96.04 as here BO=5cm and area boc=68/4=12=1/25*x this means x=24/5=4.8 so value=(5+4.8)square=(9.8)square=96.04
96.04 is the ans
96.04
96.04
96.04
96.04
correct ans : 96.04
my answer is 96.04
In triangle ADB, by using Pythagoras theorem, we can say that BD=10.Area of triangle ABD=24=1/2(10)(AE), thus, AE=x=4.8.And as O is the mid-point of BD, DO=z+y=5. Therefore, (x+y+z)^2=(4.8+5)^2=96.04
(x+y+z)power2 =100
Log in to reply
true
2z+2y=10 & (z+y=5) _(1) ((2z+y)^2)+(x^2)=64 4z^2+y^2+4yz+x^2=64 ((5-z)^2 -z^2=11 25+z^2-10z=11 z=7/5 y=(18/5) x=(24/5) z+y+x=(7/5)+(18/5)+(24/5)) z+x+y=10
(z+x+y)^2=100 unit
Log in to reply
true
SOLVE THIS PROBLEM
SOLVE THIS PROBLEM
96.04
96.04
96.04
96.04
96.04
96.04
121
The answer is 289
121
96 should b d answer
2401/25
ans is 84