Substitution easy question

Hello, could anyone help me a bit? I don't know how I could determine that g' measures how much a small interval shrinks or stretches from that graph. And the step in derivation marked with red arrow.

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

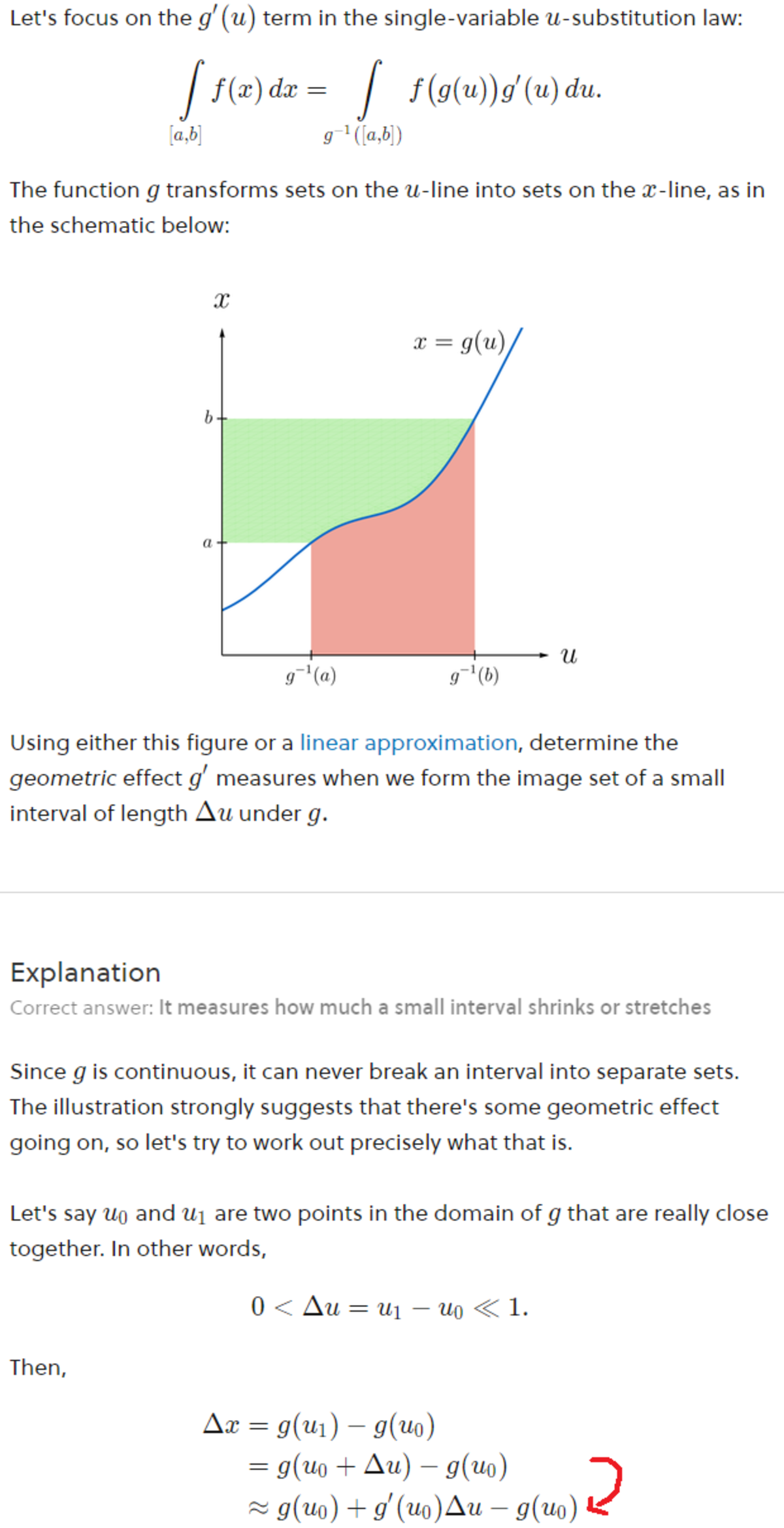
Hi Nezajem123 Nezajem123, I believe you're referring to this problem.

the reasoning goes like this:

The (infinitesimal) change in $x$ ( $\Delta x$ ) is the difference between the images of the corresponding endpoints of the interval along the $u$ direction under $g$ . In short, $\Delta x = g(u_1)-g(u_0)$ with $\Delta u = u_1-u_0$ .

We want to get a relationship between $\Delta x$ and $\Delta u$ from this expression. We start by writing $u_1$ as $u_0+ \Delta u$ , which implies $\Delta x = g(u_0+\Delta u) - g(u_0)$ . Because $\Delta u$ is so very small, we can use a linear approximation to replace $g(u_0 +\Delta u )$ by $g(u_0) + g’(u_0) \Delta u$ . This implies that $\Delta x \approx g(u_0) + g’(u_0) \Delta u - g(u_0)$ , and so $\Delta x \approx g’(u_0) \Delta u$ . Another way of expressing this is as $\Delta x/ \Delta u = g’(u_0)$ , so $g’(u_0)$ measure how much $g$ stretches/shrinks small intervals along the $u$ -direction into small intervals in the $x$ -direction.

Hope that helps!

Brilliant Mathematics Staff - 1 year ago

Thank you very much. The step I didn't catch is linear approximation, another quiz solved it for me :) https://brilliant.org/practice/linear-approximation/?p=1

nezajem123 nezajem123 - 12 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$