Sum of Harmonic Series

It is well known that the sum of a harmonic series does not have a closed form. Here is a formula which gives us a good approximation.

We need to find the sum of the following series

\[\dfrac{1}{a}+\dfrac{1}{a+d}+\dfrac{1}{a+2d}+\ldots+\dfrac{1}{a+(n-1)d}\]

Consider the function $f(x)=\frac{1}{x}$ , we intend to take middle riemann sums with rectangles of width $d$ starting from $x=a$ to $x=a+(n-1)d$ .

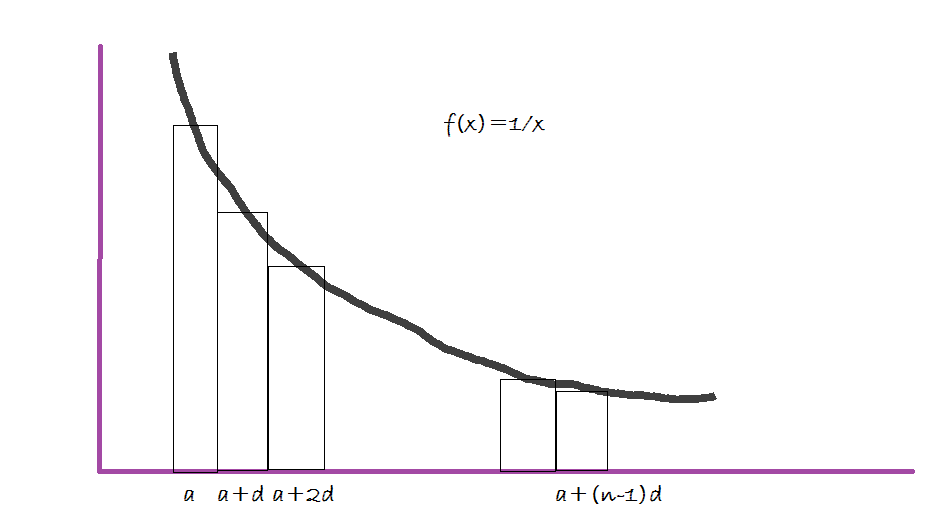
Each rectangle in the figure has a width $d$ . The height of the $i\text{th}$ rectangle is $\frac{1}{a+(i-1)d}$ . The sum of the area of the rectangles is approximately equal to the area under the curve.

Area under f(x) from $x=a-\frac{d}{2}$ to $x=a+\left(n-\frac{1}{2}\right)d \approx\displaystyle\sum_{n=1}^{n} \frac{d}{a+(n-1)d}$

$\large\Rightarrow \int_{a-\frac{d}{2}}^{a+\left(n-\frac{1}{2}\right)d} \dfrac{\mathrm{d}x}{x}\approx \displaystyle\sum_{n=1}^{n} \frac{d}{a+(n-1)d}$

Let $S_n =\displaystyle\sum_{n=1}^{n} \frac{1}{a+(n-1)d}$

$\large\ln\dfrac{2a+(2n-1)d}{2a-d}\approx d\times S_n$

$\large\boxed{\Rightarrow s_n\approx\dfrac{\ln\dfrac{2a+(2n-1)d}{2a-d}}{d}}$

Note

Apologies for the shabby graph.
$d\neq 0$

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Thanks! This is a very good and useful note.

Akshay Yadav - 5 years, 8 months ago

Thanks. :)

Aneesh Kundu - 5 years, 7 months ago

Hey how you have assigned limit of $x$ can you please clarify

Atul Shivam - 5 years, 7 months ago

$x$ varies from $a-\frac{d}{2}$ to $a+\left(n-\frac{1}{2}\right)d$ .

yaa ,I got this but also you can't use this formula for finding sum of similar terms

i.e. $S_n= \frac {1}{2}+ \frac {1}{2}+ \frac {1}{2}+ \frac {1}{2}+.... \frac {1}{2}(n^{th} term)$ as common difference is $0$ so it will be in indeterminate form

@Atul Shivam – Thanks for the suggestion, I added this point in the note.

@Aneesh Kundu – by the way is it real???

@Atul Shivam – This formula gives really good approximations when $d\rightarrow 0$ or for large values of $n$ with a not so big $d$ .

@Aneesh Kundu – Yes Absolutely

@Aneesh Kundu – Just followed you :-)

@Aneesh Kundu – I mean to is it original(your own)???

@Atul Shivam – Nope, its not purely original. I was reading about the convergence tests and I happened came across the Integral test, which inspired this note.

@Aneesh Kundu – it's really fantastic

@Atul Shivam – Thanks. :)

your above expression will be incorrect when $\boxed{2a=d}$

In this case calculate the sum from $a_2$ to $a_n$ , using the given formula and then add $a_1$ to both sides.

How can area under that curve=d×Sn ??here d is denoted as width

Emran Hossain - 5 years, 4 months ago

Area under the curve $A=\frac{1}{a} d +\frac{1}{a+d} d+ \frac{1}{a+2d} d \ldots$ $\frac{A}{d}= ( \frac{1}{a}+ \frac{1}{a+d} \ldots )$ $A=d\dot S_{n}$

Aneesh Kundu - 5 years, 4 months ago

Ohoo now i understand clearly. Thanks bro...

@Aneesh Kundu I have just added your formula to Harmonic Progression wiki. I have also added important points from your discussion with Atul. You can also contribute to the wiki.

Akshay Yadav - 5 years, 3 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$