Supporting at 2 points

I have a problem calculating tensions on 2 ropes

acting in the same direction supporting an object at 2 points

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

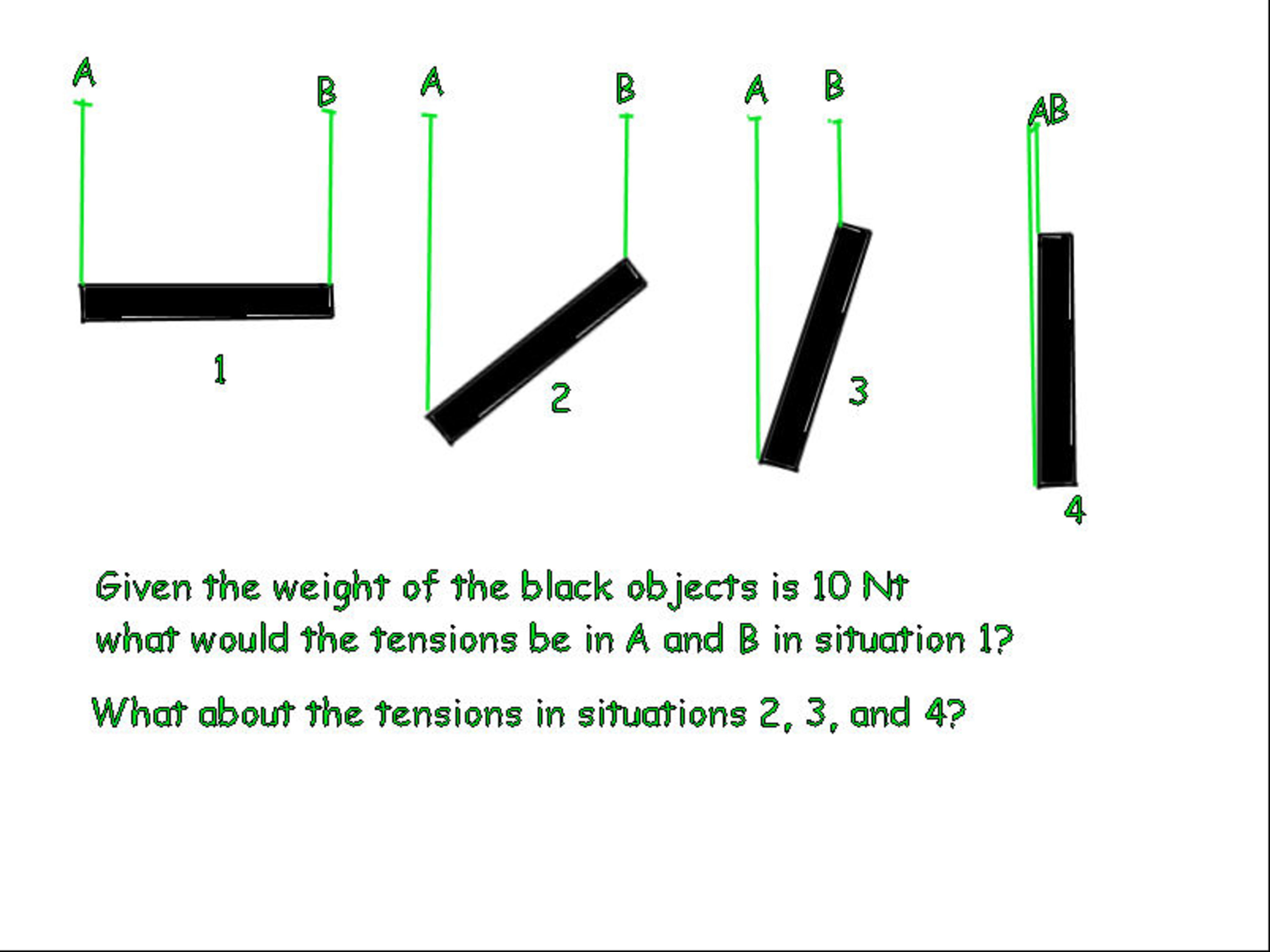
The block is in equilibrium in each case. This means that the net force and the net torque on the block are both zero. Balancing the torques about the center of mass, and the left and right points of suspension will give a set of linear equations which can be used to find the tensions. Do you know how to proceed now?

Pranshu Gaba - 3 years, 6 months ago

Suppose the block has uniform density and has a mass of 1 kg and it has the slope of 1, what are the tensions on each of the vertical ropes?

Guiseppi Butel - 3 years, 6 months ago

I' m sorry, I don't. The tangential forces on each end are equal and the arms are equal therefore the tensions will be equal , however my intuition concludes that there is a greater tension on the rope attached to the higher end of the bar.

Guiseppi Butel - 3 years, 6 months ago

Your answer is correct. It may seem unintuitive, but as long as the ropes are vertical and the rod is uniformly distributed, the tension will be equal in both ropes. If the rod is tilted by angle $\theta$ , you may look at it as a horizontal rod of length $l \cos \theta$ .

Pranshu Gaba - 3 years, 6 months ago

@Pranshu Gaba – I don't believe that the tensions on both ropes are equal regardless of the bars orientation. If the bar is vertical the rope attached to the top will support the total weight and the other will have 0 tension. What am I missing?

Guiseppi Butel - 3 years, 6 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$