Symmetry in quadratic equations mod n

Inspired by this problem

The problem is about a quadratic function modulo 53, and it asks for which function values you can compose this function multiple times to get a result of 18.

What's interesting, is that the solutions come in pairs whose sum is always 51, and actually $\forall a,b \in (\mathbb{Z}/53\mathbb{Z}) (a+b=51 \Rightarrow f(a)=f(b))$ with the ring of integers modulo 53 $\mathbb{Z}/53\mathbb{Z}$.

Is this a consequence of mod 53 or always true for quadratic equations?

This is the graph that shows for each value what the function gives and where you would continue and it is really symmetric and I think beautiful (except for a few links that break the patterns)

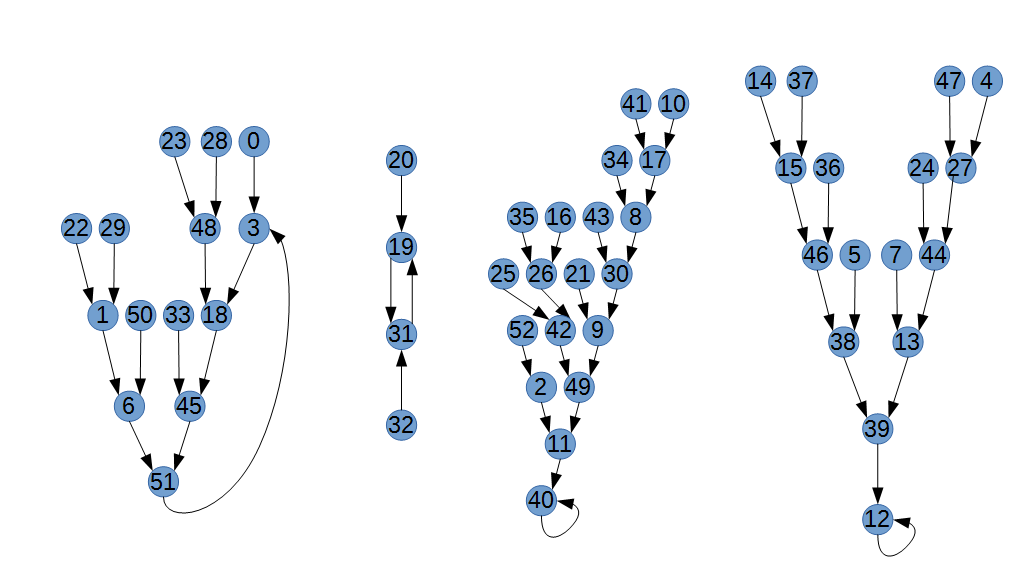
Proof

So this is a proof for this particular polynomial

$(51-n)^2+2(51-n)+3$

$= n^2-104n+2706$

$\equiv (n^2 \pmod {53}) + (-104n \pmod {53}) + (2706 \pmod {53})$

$\equiv n^2+2n+3 \pmod {53}$

and for some prime $p$

$((p-2)-n)^2+2((p-2)-n)+3$

$= n^2-2pn+2n+p^2-2p+3$

$\equiv (n^2 \pmod p) + (-2pn+2n \pmod p) + (p^2-2p+3 \pmod p) \equiv (n^2 \pmod p) + (2n \pmod p) + (3 \pmod p)$

$\equiv n^2+2n+3 \pmod p$

In general

For a general quadratic polynomial $an^2+bn+c \pmod p$ with $a,b,c \in \mathbb{N}, p \in \mathbb{P}, a \neq 0$

$a((p-2)-n)^2+b((p-2)-n)+c$

$= ((a)n^2+(4a-2ap-b)n+(ap^2+bp-4ap+c-2b+4a))$

$\equiv (an^2 \pmod p) + (4an-2apn-bn \pmod p) + (ap^2-4ap+bp+4a-2b+c \pmod p)$

$\equiv (an^2 \pmod p) + (4an-bn \pmod p) + (4a-2b+c \pmod p)$

$\equiv ((an^2) + (4an-bn) + (4a-2b+c)) \pmod p$

For this to be congruent to the original polynomial, we require

$a \equiv a \pmod p$

$4a-b \equiv b \pmod p$

$4a-2b+c \equiv c \pmod p$

The first condition is always true, the other two are equivalent and can be rewritten as

$2a \equiv b \pmod p$

So $c$ actually has no influence and we have only one condition on the coefficients (and $p$ must be prime).

Degree 4

Let's try to do the same thing with a polynomial of degree 4 (because 3 doesn't work well), so $an^4+bn^3+cn^2+dn+e$ with $a,b,c,d,e \in \mathbb{N}, p \in \mathbb{P}, a \neq 0$

$a(p-2-n)^4+b(p-2-n)^3+c(p-2-n)^2+d(p-2-n)+e$

$= (\text{stuff}) \cdot p + an^4 + 8an^3-bn^3 + 24an^2-6bn^2+cn^2 + 32an-12bn+4cn-dn + 16a-8b+4c-2d+e$

$\equiv ((a)n^4 + (8a-b)n^3 + (24a-6b+c)n^2 + (32a-12b+4c-d)n + (16a-8b+4c-2d+e)) \pmod p$

By equating coefficients, we get

$a \equiv a \pmod p$

$8a-b \equiv b \pmod p$

$24a-6b+c \equiv c \pmod p$

$32a-12b+4c-d \equiv d \pmod p$

$16a-8b+4c-2d+e \equiv \pmod p$

Again, the first congruence is trivial and the second and third are equivalent. By pluging the second into the fourth and fifth, we find that they are also equivalent. So, we end up with two congruences

$4a-b \equiv 0 \pmod p$

$-2b+2c-d \equiv 0 \pmod p$

If we want we can pick some numbers, maybe $a=1$ to have a normalized polynomial, then $b$ has to be $4$. For $c$ and $d$, we can pick $5$ and $2$ and since $e$ is without any restriction, let's make it nice and take $e=3$. This gives the polynomial

$f(n) = n^4+4n^3+5n^2+2n+3$

and if we try we see that it really follows our rule

$\forall a,b \in (\mathbb{Z}/53\mathbb{Z}) (a+b=51 \Rightarrow f(a)=f(b))$