If R is the radius of the bigger semi-circle and r1,r2 are the radii of the smaller semi-circles then,
Areaoftheshadedregion=2R2cos−1(1−R48C)−R22CR4−4CwhereC=(R2−r1r2)r1r2
This discussion board is a place to discuss our Daily Challenges and the math and science
related to those challenges. Explanations are more than just a solution — they should
explain the steps and thinking strategies that you used to obtain the solution. Comments
should further the discussion of math and science.
When posting on Brilliant:
Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.
Markdown
Appears as
*italics* or _italics_
italics
**bold** or __bold__
bold
- bulleted - list
bulleted
list
1. numbered 2. list
numbered
list
Note: you must add a full line of space before and after lists for them to show up correctly
Using just "elementary" geometry:
Let r1 be the radius of the left semicircle and r2 the radius of the right one. WLOG we take r1≥r2. Denote by d=OD the apothem of the cord FE. Denote by K, O and L the centers of the three semicircles as seen in the figure. Let G, H be the points of tangency of the cord with the semicircles. Let LN and OP be perpendicular to KG.
Then we have,
R=r1+r2⇒KO=AO−AK=R−r1=r2
Since right triangles PKO and NKL are similar,
KOPK=KLNK⇒r2r1−d=r1+r2r1−r2⇒r2r1−d=Rr1−r2
which solves to
d=R1(2r12−2Rr1+R2)
Now, the area of the circular segment gets maximised when its cord is maximised, which in turn occurs when the apothem d is minimised.
The latter happens when r1 equals the x-coordinate of the vertex of the parabola y=R1(2x2−2Rx+R2), i.e. when r1=2R.
In this case, d=2R which is the apothem of the inscribed equilateral triangle, thus ∠FOE=32π and the maximal area of the circular segment is
A=2132πR2−21R2sin32π=(3π−43)R2
In general, the area of the circular segment can be expressed as
A=2R2cos−1(2R2d2−1)−dR2−d2
where
d=R1(2r12−2Rr1+R2)=R1(r12+r22)
Then,
Area=2R2cos−1(1−R48C)−R22CR4−4C=2R2cos−1(R22d2−1)−dR2−d2whereC=(R2−x(R−x))x(R−x),d=R2x2−2Rx+R2
The Graph of the equation looks like this
The maxima of the graph is x=2R (solved by @Thanos Petropoulos )
⇒A=R2(3π−43)
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
@Charley Shi @Hosam Hajjir @David Vreken @Thanos Petropoulos @Valentin Duringer @Fletcher Mattox @Mahdi Raza @Aryan Sanghi
Neat problem. How did you arrive at the area of the shaded region? Area of the sector - triangle = Segment?
Log in to reply
The whole Process:
I took the whole case in a coordinate plane with the center of the large semi-circle as the origin and it's diameter as x-axis.
Then the equation of the tangent became : y=2r1r2x(r2−r1)+r12+t22
Then I found the length of PQ=R4R2−r1r2r1r2
It is then easier to find the area of the shaded region as you now know the length of the chord...
This Might Help to understand better
Log in to reply
Oh wow! That’s well made
Using just "elementary" geometry: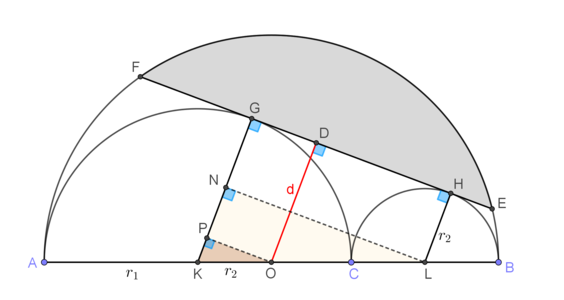 Let r1 be the radius of the left semicircle and r2 the radius of the right one. WLOG we take r1≥r2. Denote by d=OD the apothem of the cord FE. Denote by K, O and L the centers of the three semicircles as seen in the figure. Let G, H be the points of tangency of the cord with the semicircles. Let LN and OP be perpendicular to KG.
Then we have,
Let r1 be the radius of the left semicircle and r2 the radius of the right one. WLOG we take r1≥r2. Denote by d=OD the apothem of the cord FE. Denote by K, O and L the centers of the three semicircles as seen in the figure. Let G, H be the points of tangency of the cord with the semicircles. Let LN and OP be perpendicular to KG.
Then we have,
R=r1+r2⇒KO=AO−AK=R−r1=r2 Since right triangles PKO and NKL are similar, KOPK=KLNK⇒r2r1−d=r1+r2r1−r2⇒r2r1−d=Rr1−r2 which solves to
d=R1(2r12−2Rr1+R2) Now, the area of the circular segment gets maximised when its cord is maximised, which in turn occurs when the apothem d is minimised. The latter happens when r1 equals the x-coordinate of the vertex of the parabola y=R1(2x2−2Rx+R2), i.e. when r1=2R.
In this case, d=2R which is the apothem of the inscribed equilateral triangle, thus ∠FOE=32π and the maximal area of the circular segment is
A=2132πR2−21R2sin32π=(3π−43)R2
In general, the area of the circular segment can be expressed as
A=2R2cos−1(2R2d2−1)−dR2−d2 where d=R1(2r12−2Rr1+R2)=R1(r12+r22)
Log in to reply
Very neat solution, I didn't even thought of Apothem!
I found a mistake in my previous formula so fixed it, now it's absolutely correct
We can substitute r1=x,r2=R−x
Then, Area=2R2cos−1(1−R48C)−R22CR4−4C=2R2cos−1(R22d2−1)−dR2−d2 where C=(R2−x(R−x))x(R−x),d=R2x2−2Rx+R2 The Graph of the equation looks like this
The maxima of the graph is x=2R (solved by @Thanos Petropoulos ) ⇒A=R2(3π−43)