Tear the question paper, then throw it away

After the APMOPS, here are some questions that I translated:

A magician made a six-digit number $A$ , and the digit sum of $A$ be $B$ . The magician called out a spectactor to evaluate $A$ - $B$ . The spectactor said out 5 numbers, namely $0,2,4,6$ and $8$ .The magician successfully revealed the last number. What number is it? Explain your reason.

*Bonus question: Find the minimum and maximum value for $A$ .

The eight vertexes of an octagon are attached with circles, each required to fill up the numbers from 1 to 8. Can the sum of four consecutive attaching circles be:

a)larger than 16?

b) larger than 17?

If possible, find a way of doing so; if not, explain your reason.

Wong cycled from station A to station B. Buses form station A and B each give out a bus at the same interval time (e.g. when station A gives out a bus every 30 minutes, station B does the same), but at different times. Every 6 minutes Wong meets up with a bus coming from the opposite, and every 9 minutes he is overtaken by a bus traveling at the same direction with him. It is known that all the buses from stations A & B take 50 minutes to travel to the other side ( it means that buses from station A travel 50 minutes to station B, and vice versa ). How long does it take for Wong to travel from station A to B?

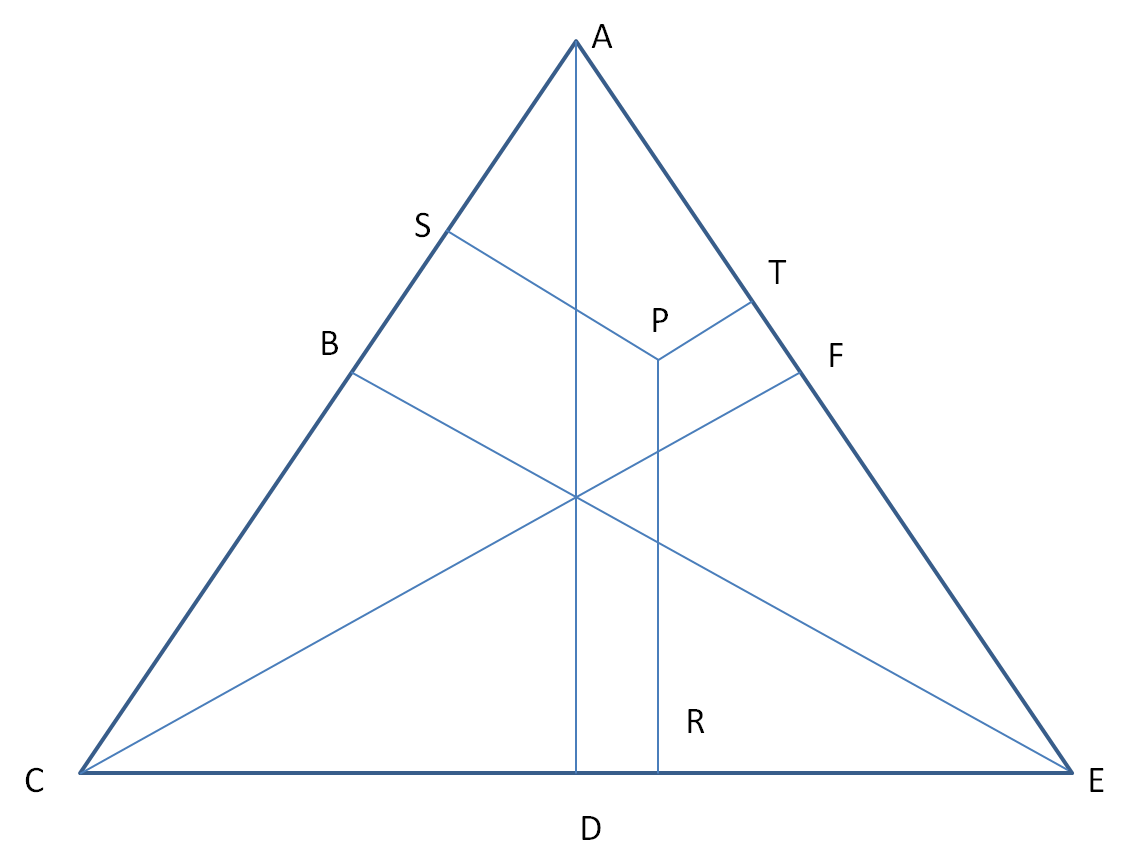
4.In the figure below, 3 different heights of the triangle move from the bases to the vertexes of the triangle. P is a point in the triangle such that another 3 lines move from point P to the triangle, causing each of the lines to be parallel with AD, BE and CF respectively. If AD=2010 cm, BE= 2013 cm, CF = 2016 cm and PR = 1005 cm, PS= 671 cm, find the length of PT. (Oh, and I forgot, each line extending to the base is straight, or 90 degrees)

Feel free to discuss! Enjoy!

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Q1: The last number is $7$ . $A$ can be expressed as $(10^5\times a+10^4\times b+10^3\times c+10^2\times d+10\times e+f)$ where $a,b,c,d,e$ and $f$ are the digits of $A$ .

$B$ can be expressed as $(a+b+c+d+e+f)$ .

Now, $A-B=99999a+9999b+999c+99d+9e$ .

$A-B=9(11111a+1111b+111c+11d+e)$ implying that $A-B$ is a multiple of $9$ .

Since, $A-B$ is a multiple of $9$ , the digit sum of $A-B$ must also be divisible by $9$ (Divisibility Test of $9$ ).

Now, we are provided with $5$ digits of $A-B$ and we have to find the sixth one. The sum of these $5$ digits comes out to be $20$ and so for $A-B$ to be divisible by $9$ , the sixth digit should be $7$ so that it sums out to be a multiple of $9$ .

NOTE: There is a trick here. If the spectator would have called out $2,4,6,7$ and $8$ and then we were to find out the sixth digit, we could have $2$ different answers namely $0$ and $9$ . Can you figure it out why?

Yash Singhal - 6 years ago

Because 2+4+6+7+8 IS a multiple of 9

Bryan Lee Shi Yang - 6 years ago

Yes, it has to be a multiple of $9$ . This is true for all numbers and can be generalized easily for $n$ -digit numbers.

Q4 is 336.

Saya Suka - 2 years ago

Q3 is 250 minutes.

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$