Tessellate S.T.E.M.S - Physics - School - Set 1 - Subjective Problem

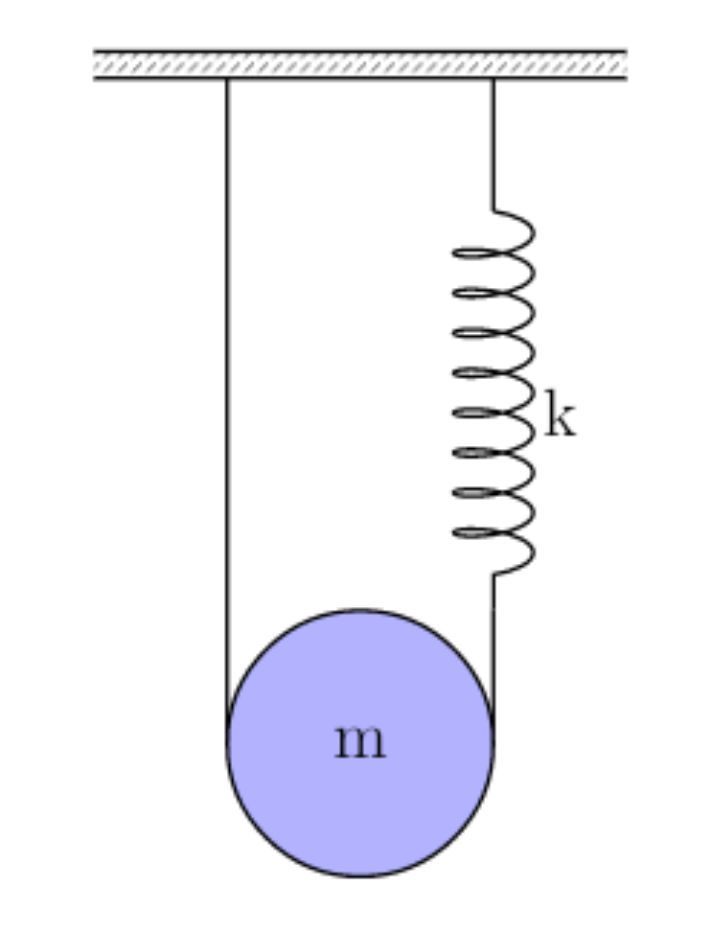
A pulley in the form of a circular disc of mass $m$ and radius $r$ has the groove cut all along the perimeter. A string whose one end is attached over to the ceiling passes over this disc pulley and its other end is attached to a spring of spring constant k. The other end of the spring is attached to the ceiling as shown in the figure. Find the time period of vertical oscillations of the centre of mass assuming that the string does not slip over the pulley?

This problem is a part of Tessellate S.T.E.M.S.

#Mechanics

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

$\omega ^2=\frac {4kx}{1+\frac {I_{cm}}{mR^2}}$ ,therefore here $\omega =\sqrt \frac {8k}{3m}$

Spandan Senapati - 3 years, 5 months ago

how u derived the first formula

Arun Palaniappan - 3 years, 5 months ago

Refer HC Verma. The question had been directly copied from there

Spandan Senapati - 3 years, 5 months ago

@Spandan Senapati – your answer is dimensionally incorrect it would be better if u correct it

omswostik mishra - 3 years, 5 months ago

@Omswostik Mishra – I am not used to doing such mistakes.Kindly check it correctly the answer is correct as are the dimensions.

Spandan Senapati - 3 years, 5 months ago

2pi_/(3m/8k)

Arunava Das - 3 years, 5 months ago

When studying at school, I always do not have enough time for the normal completion of my homework. Sometimes you have to come up with new ways to solve this problem, https://edubirdie.com/words-to-minutes-converter - here you can find words to minutes converter and other useful tools that will help you quickly deal with all problems and save your time.

Jamie Henry - 1 year, 9 months ago

π(m/k)^(1/2)

Ankitesh kumar - 3 years, 5 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$