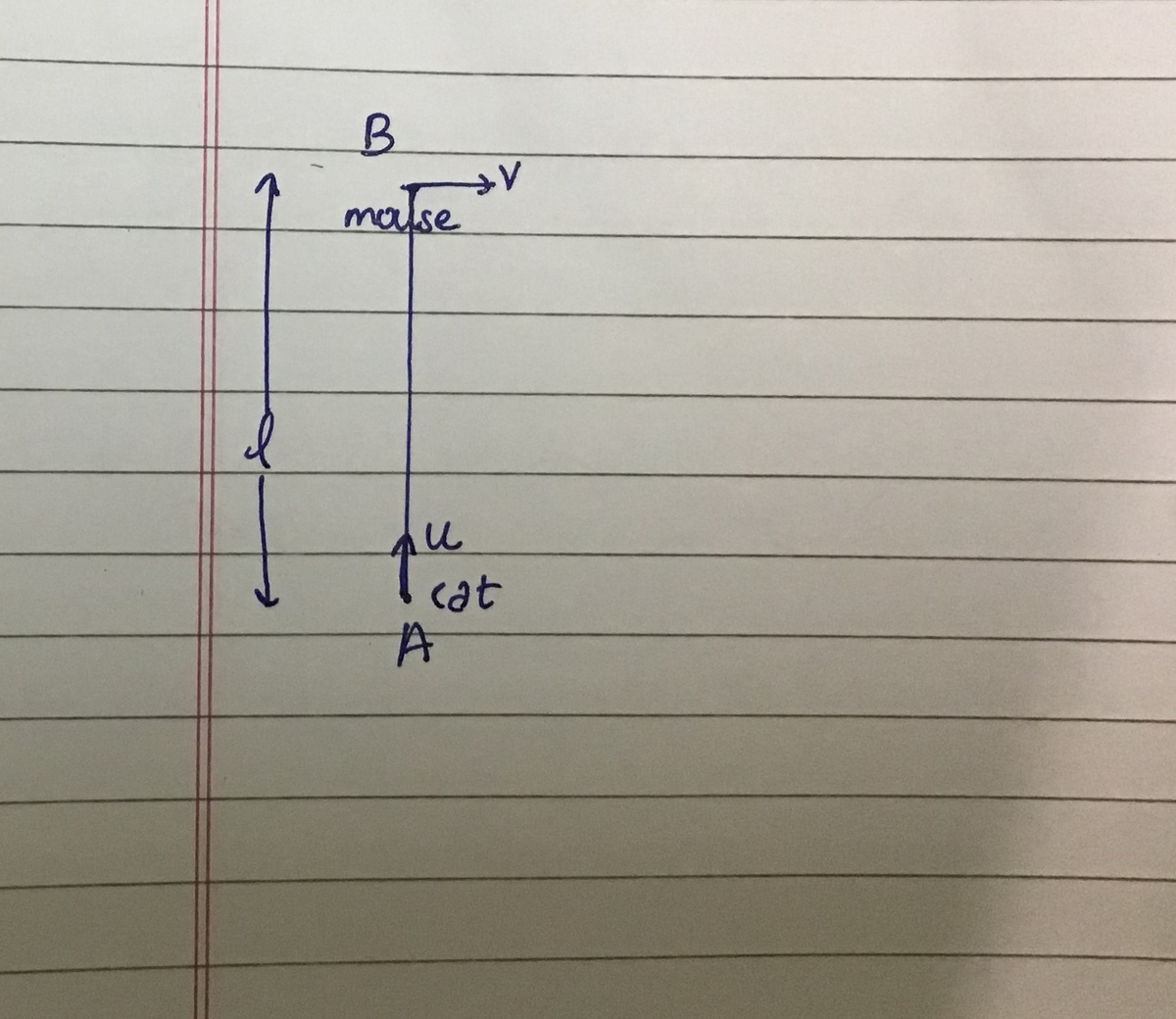
The cat mouse trajectory

A cat is initially at A and a mouse at B. The mouse starts moving perpendicular to AB with constant speed v.The cat moves towards the mouse with constant speed u, in order to catch it in such a way that it’s velocity vector always points towards the mouse. Find the trajectory traced by the cat.

#Mechanics

Note by Ayan Sharma
1 year, 6 months ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

The trajectory can be obtained by solving the following set of coupled differential equations:

dxdt=u(vt−x)(vt−x)2+(L−y)2\frac{dx}{dt} = \frac{u(vt-x)}{\sqrt{(vt-x)^2 + (L-y)^2}} dydt=u(L−y)(vt−x)2+(L−y)2\frac{dy}{dt} = \frac{u(L-y)}{\sqrt{(vt-x)^2 + (L-y)^2}}

x(0)=y(0)=0x(0) = y(0) = 0

The way these equations are derived are as such:

  • At a general time tt the coordinates of the mouse are P1: (vt,L)P1: \ (vt,L) and that of the cat are P2: (x,y)P2: \ (x,y).
  • Say the velocity vector of the cat makes an angle θ\theta with the horizontal. Then the velocity vector is along the line joining the points P1P1 and P2P2.
  • So, this gives three equations:

tan⁡θ=L−yvt−x\tan{\theta} = \frac{L-y}{vt-x} dxdt=ucos⁡θ\frac{dx}{dt} = u\cos{\theta} dydt=usin⁡θ\frac{dy}{dt} = u\sin{\theta}

Eliminating θ\theta gives the equations listed above. This set of equations needs to be solved numerically. If you want more information like plots, etc., I will post if requested.

Karan Chatrath - 1 year, 6 months ago
×

Problem Loading...

Note Loading...

Set Loading...