The continuity of Thomae's Function

The Thomae's function is an area of great interest in real analysis. It is given by:

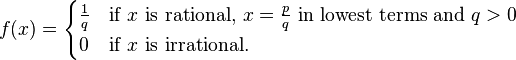
In this note, I will discuss the continuity of the function at different points in the interval [0,1]. First we shall check whether this function is continuous at rational points in the domain or not. Let $c\in Q$, the set of rationals. Then $f(c)\neq 0$. Now we attempt to choose a sequence ${ \left( { x }_{ n } \right) }_{ n\ge 1 }$ of irrationals in [0,1] which converge to c. Clearly, such a sequence can always be chosen owing to the density property of irrationals. Then ${ \left( { f(x }_{ n }) \right) }_{ n\ge 1 }$ is a constant sequence (the zero sequence), which is clearly not convergent to f(c). So the function is discontinuous at every rational point. Now, let us choose an irrational point, say, b. So, $f(b)=0$ Examining the continuity of the function at irrational points is a bit tricky and needs use of the $\varepsilon -\delta$ criterion of continuity. We see that the $\frac { 1 }{ q }$ thing implies the need of using the Archimedean property in proving (or disproving) the continuity. According the $\varepsilon -\delta$ definition, for an arbitrary $\varepsilon >0$, we have to find a $\delta >0$ such that: $\left| x-b \right| <\delta \\ \Longrightarrow \left| f(x)-f(b) \right| =\left| f(x) \right| <\varepsilon$ Now, if we choose such an x from the irrationals then $f(x)=0$, and the above condition holds for any $\delta >0$. However the problem comes if we are to choose such an x from the rationals. But aha, the Archimedean Property comes to rescue. We see, that for any $\varepsilon >0$ $\exists { n }_{ 0 }\in N,\quad s.t.\quad \forall n\ge { n }_{ 0 },\quad n\in N,\frac { 1 }{ n } <\varepsilon$. Thus we see that each of $\frac { 1 }{ 1 } ,\frac { 1 }{ 2 } ,\frac { 1 }{ 3 } ,..,\frac { 1 }{ { n }_{ 0 }-1 }$ is greater than $\varepsilon$. Again, we see, that for any $n\in N$ there are $(n+1)$ rationals lying in [0,1], which are mapped to $\frac { 1 }{ n }$ under the Thomae's function, viz., $\frac { 0 }{ n } ,\frac { 1 }{ n } ,\frac { 2 }{ n } ,\frac { 3 }{ n } ,..,\frac { n }{ n }$. Thus for the ${ n }_{ 0 }$ that we have found, we see that there are $(n-1)$ rationals each with numerator 1, that are greater than or equal to $\varepsilon$, and hence there are ${(1+1)+(2+1)+(3+1)+..({ n }_{ 0 }-1+1)}$ many rationals which disturb the inequality $\left| x-b \right| <\delta$ and affect our choice of $\delta$. Thus we are to choose $\delta$ so as to exclude all these disturbing rationals from the open interval $\left( b-\delta ,b+\delta \right)$. This can be effected by choosing:$\delta =\frac { 1 }{ 2 } min\left\{ \left| \frac { m }{ n } -b \right| ,\quad where\quad m=0(1)n,n=1(1)({ n }_{ 0 }-1) \right\}$,i.e., making the gap of $\delta$ and b even lesser than the gap between b and the disturbing rational nearest to b. Thus we see, that for an arbitrary $\varepsilon >0$, we can find a $\delta >0$ such that: $\left| x-b \right| <\delta \\ \Longrightarrow \left| f(x)-f(b) \right| =\left| f(x) \right| <\varepsilon$. Thus Thomae's function is continuous at irrationals.