The Faded Document Puzzle

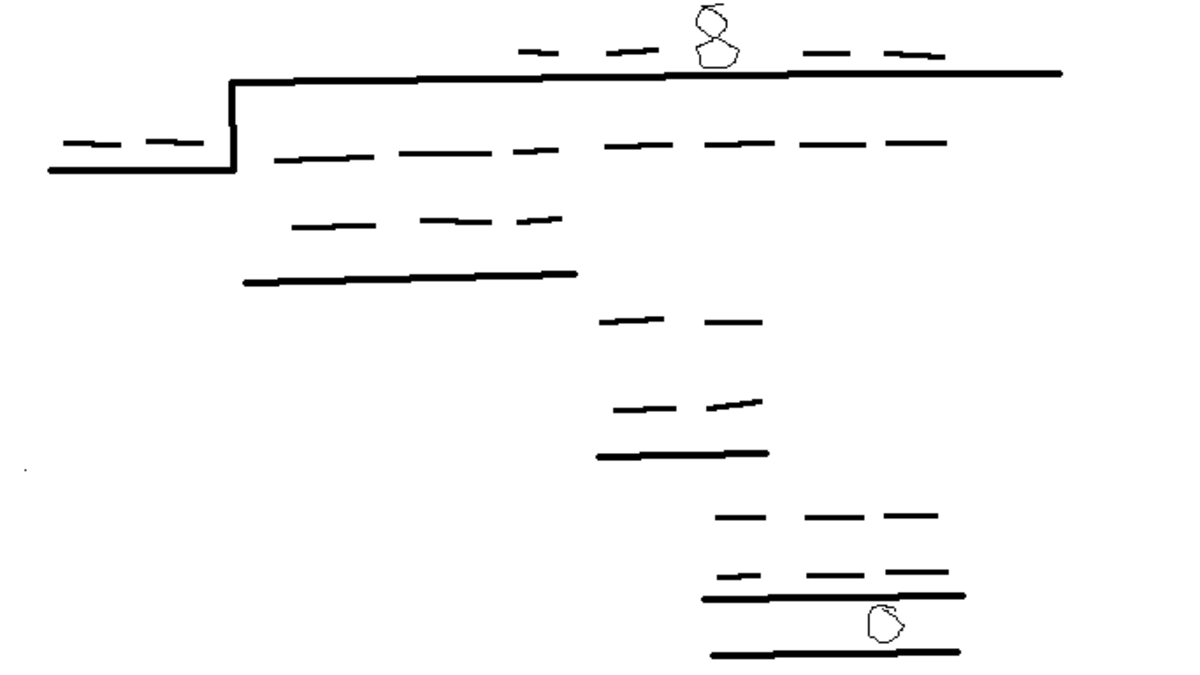
I had posted this as a problem earlier, but I think some people were easily using option analysis to solve it, so I am putting it as a note.

The task is to fill in the blanks with the right digits. Only an 8 is visible. There may be other 8s in the document.

It looks difficult, but is pretty simple. You just have to imagine you are doing long division and see what constraints arise from that.

The source is Joseph Degrazia, Math Tricks, Twisters and Riddles.

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Firstly, there should be a zero before and after the 8 in the quotient-only then is the division possible, following the rules of 'carry-down'. Next, looking at the second line of division-a 2-digit divisor multiplied by 8 gives a 2-digit number. This is only true if the divisor is 10, 11 or 12. Next, looking at the first line of division, a 2-digit divisor multiplied by a one-digit number gives a 3-digit number. This can only happen if the divisor is 12 and the first digit of the quotient is 9.12*9=108 Apply the same logic in the last line of the division. Then fill in the few remaining blanks-it becomes self-evident how to.

Sachetan Debray - 5 months, 2 weeks ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$