The Golden Ratio: 3-4-5

Here is the previous post concerning the Golden Ratio. For a collection of all the posts concerning the Golden Ratio, click #GoldenRatio below.

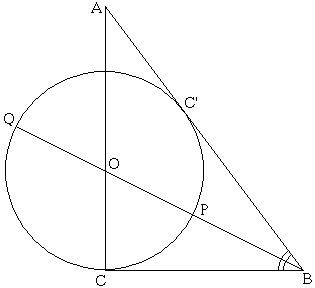
Since we have already talked about several Golden figures, we are going to delve more deeply into where exactly we can find the golden ratio in other figures. Today we will talk about the ubiquitous 3−4−53-4-5 triangle. Everyone has learned that this is the simplest of all integral right triangles. But interestingly enough, it also contains the golden ratio. Here is the construction:

Above is the triangle ABCABC with AB=5AB = 5, AC=4AC = 4, and BC=3BC = 3. Let OO be the foot of the angle bisector from BB. Draw a circle centered at OO with radius COCO. Then extend BOBO until it hits circle OO again at QQ. Let PP be the other point of intersection of these two curves. Then

PQBP=ϕ\frac{PQ}{BP} = \phi

Problem 1) Can you prove the above proposition?

Problem 2) Extra: In the figure above, there is another point C′C'. Prove that the circle OO intersects the line segment ABAB at only one point C′C'. Also, why might it be called C′C'?

Credit: Cut-the-Knot

Here is the next post.

#Geometry #Construction #CosinesGroup #Triangles #GoldenRatio

Note by Bob Krueger
7 years, 5 months ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

For problem 2, simply reflect the entire figure about ACAC. You will find the circle in the center is the incircle from an incircle's definition of being the circle with center being the intersection of the angle bisectors, and the result follows.

Daniel Liu - 7 years, 5 months ago

Log in to reply

This is probably the easiest way to prove it.

Bob Krueger - 7 years, 5 months ago

Since no one has answered the first problem, I will assume that it was either too easy or too hard. As a hint for those who thought it was hard, try using the half angle formula for tangent, but do not calculate the angles directly.

Bob Krueger - 7 years, 5 months ago
×

Problem Loading...

Note Loading...

Set Loading...