The Golden Ratio: Beginning the Geometry of

Here is the previous post concerning the Golden Ratio. For a collection of all the posts concerning the Golden Ratio, click #GoldenRatio below.

Now that we know what the golden ratio is, and why people like it, let's look at it in a geometrical sense, as the greeks would have. One definition of the golden ratio is the one that started this series, based on the golden rectangle. Another definition is as follows:

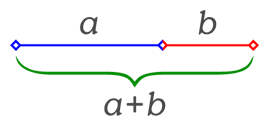
Divide a line segment into two parts. The Golden Ratio is the ratio of the larger part to the whole, when that ratio is also equal to the ratio of the smaller part to the larger part.

Basically, imagine the line segment pictured above. When we set the two proportions equal to each other we get

a+ba=ab=ϕ\frac{a+b}{a} = \frac{a}{b} = \phi

Solving this like we did in the first post will indeed yield 1+52\frac{1+\sqrt{5}}{2}.

Since this post is kind of short too, I'll add in a teaser. If someone can effectively answer my question before this evening (in the next ten hours), I'll put up the tomorrow's post tonight.

Here's the question: What are the lengths of the diagonals of a regular unit pentagon? Prove it.

See the full proof in here

#Geometry #CosinesGroup #GoldenRatio #EpsilonGroup

Note by Bob Krueger
7 years, 5 months ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

Click here for the image

ABCDE is a regular pentagon with side length 1

AD,AC & EB is the diagonals of the pentagon

AD intersect EB at point F,AC intersect EB at point G

AF=EF=y, so △AEF\bigtriangleup AEF is a isosceles triangle

△DEF\bigtriangleup DEF is a isoceles triangle, so ED=FD=1 ED=FD=1

So,the diagonals=1+y = 1+y

∠FAE=∠AEF=∠EDF=36∘\angle FAE=\angle AEF=\angle EDF=36^\circ

∠AED=∠AFE=108∘\angle AED=\angle AFE=108^\circ

△AFE∼△ADE \bigtriangleup AFE \sim \bigtriangleup ADE So that, 1+y1=1y \frac{1+y}{1}=\frac{1}{y}

a+ba=ab=ϕ \frac{a+b}{a}=\frac{a}{b}=\phi

By substituting a=1,b=ya=1, b=y

We get, 1+y1=1y=ϕ \frac{1+y}{1}=\frac{1}{y}=\phi

The length of the diagonals is ϕ≈1.618 \phi \approx 1.618

Lim Zi Heng - 7 years, 5 months ago

Log in to reply

Is there another way?

Bob Krueger - 7 years, 5 months ago

Log in to reply

An alternate way is to apply cosine rule in one of the triangles.

If a is the length of the diagonal, use cosine rule to get a2=2.618 a^2 = 2.618approximately equal to 1+ϕ1 + \phi and from here recall that 1+ϕ=ϕ21 + \phi = \phi^{2}it is easy to get a=ϕa = \phi .

Harman Kahlon - 7 years, 5 months ago

Log in to reply

@Harman Kahlon – Right. This is the way I first discovered it.

Bob Krueger - 7 years, 5 months ago

this is the way I think

Lim Zi Heng - 7 years, 5 months ago

I will attach an image after I know how to attach an image

Lim Zi Heng - 7 years, 5 months ago

I attach the image already

Lim Zi Heng - 7 years, 5 months ago

it is very interesting to know that the equivalent resistance of thiscircuit where all the resistances are 1 ohm is GOLDEN RATIO. I think this is because of the existence of the ratio in the radical form

ayush chowdhury - 7 years, 5 months ago

Log in to reply

Very interesting indeed.

Bob Krueger - 7 years, 5 months ago
×

Problem Loading...

Note Loading...

Set Loading...