The Golden Ratio: Golden Triangles

Here is the previous post concerning the Golden Ratio. For a collection of all the posts concerning the Golden Ratio, click #GoldenRatio below. A knowledge of trigonometry would be useful in understanding this post.

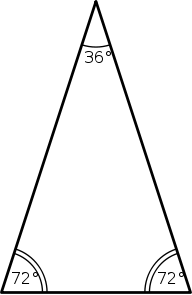
The last question of the previous post inspired this one. There are certainly more interesting things that result from this pentagon than we would expect. For example, take $\Delta ABF$, or an isoceles triangle with angles $36^{\circ}$, $72^{\circ}$, $72^{\circ}$. Extend the angle bisector from one of the larger angles to the other side. What do you get? If you draw a picture (strongly encouraged) and do some angle chasing, you will find that one of the triangles made is similar to the original triangle! The other resulting triangle should be a familiar $108^{\circ}-36^{\circ}-36^{\circ}$ triangle. Note what happens too when you divide the $108^{\circ}$ angle into $72^{\circ}$ and $36^{\circ}$. What if you trisect the $108^{\circ}$ angle in this triangle? What other dissections can you make? Feel free to post your findings below. The acute triangle is called the golden triangle, while the obtuse triangle is called the golden gnomon.

In my examinations of these figures, I found this especially interesting bit. Let's apply the Law of Cosines on the golden triangle with respect to the $36^{\circ}$ angle:

$1^2 = \phi^2 + \phi^2 - 2 \cdot \phi \cdot \phi \cdot \cos 36^{\circ}$

$\rightarrow 1 = 2\phi^2 (1-\cos 36^{\circ})$

$\rightarrow \cos 36^{\circ} = 1 - \frac{1}{2\phi^2}$

$= 1 - \frac{1}{2 \left( \frac{1 + \sqrt{5}}{2} \right)^2}$

$= 1 - \frac{2}{\left(1 + \sqrt{5}\right)^2}$

$= 1 - \frac{2}{6 + 2\sqrt{5}}$

$= 1 - \frac{1}{3 + \sqrt{5}}$

$= 1 - \frac{3 - \sqrt{5}}{4}$

$= \frac{4 - 3 + \sqrt{5}}{4}$

$= \frac{1}{2} \phi$

Woah! We used to think that sines and cosines of only $30^{\circ}$, $45^{\circ}$, and $60^{\circ}$ (and halves, sums, and multiples thereof) could be expressed nicely. Not any more!

Problem 1: What are the areas of the golden gnomon and golden rhombus? Is there such a thing as a "golden rhombus?" Can you use this information to find the area of a unit pentagon? Post your findings below.

Problem 2: Make a table or list of the sines, cosines, and tangents of some sums and multiples of $36^{\circ}$. Post your findings below.

Click here to learn about another triangle involving the golden ratio.