The Golden Ratio: Kepler Triangle

Here is the previous post concerning the Golden Ratio. For a collection of all the posts concerning the Golden Ratio, click #GoldenRatio below.

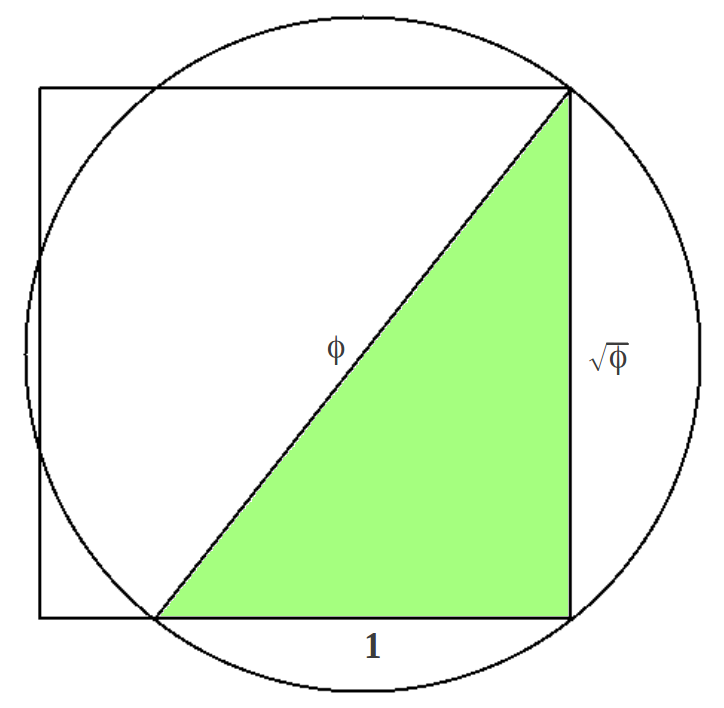
I propose a question for you: If the smallest side of a right triangle is 11, and the sides are in geometric proportion, what are the other sides of the triangle? Try and answer this question yourself before reading further.

If the smallest side is 11, we can call the next leg rr and the hypotenuse r2r^2. By the Pythagorean Theorem, we know that 12+r2=r41^2 + r^2 = r^4. To make this equation look especially familiar, we will use the substitution a=r2a=r^2. Then 1+a=a21 + a = a^2. Thus a=r2=ϕa = r^2 = \phi and r=ϕr = \sqrt{\phi} are the remaining two sides of the triangle. This is called a Kepler Triangle.

The Kepler Triangle has interesting properties. Half the base, height, and slant height of the great pyramid at Giza form a Kepler Triangle.

Next, let's construct a square with side length ϕ\sqrt{\phi} and the circumcircle of our Kepler Triangle. What are the perimeters of each? Well, the square has perimeter 4ϕ≈5.0884\sqrt{\phi} \approx 5.088 and the circumcircle (whose diameter is the hypotenuse of the Kepler Triangle) has circumference πϕ≈5.083\pi \phi \approx 5.083. These are strikingly similar! In fact, the error between them is less than a tenth of a percent! From this, we can get the approximation coincidence

π≈4ϕ\pi \approx \frac{4}{\sqrt{\phi}}

The next post

#Geometry #CosinesGroup #GoldenRatio

Note by Bob Krueger
7 years, 5 months ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

I didn't know that this triangle had a name! Learning something new everyday. Thanks!

Calvin Lin Staff - 7 years, 5 months ago

Log in to reply

Kepler said that the two most interesting things from geometry were the Pythagorean Theorem and the golden ratio (from Wikipedia). So this special triangle is named after him.

Bob Krueger - 7 years, 5 months ago

Woah

faraz masroor - 7 years, 5 months ago

It is the real information. Really nice,

Muh. Amin Widyatama - 7 years, 5 months ago

Proof that the shortest edge length of a Kepler right triangle is equal in measure to the circumference of a circle with a diameter that is equal in measure to 1 quarter of the second longest edge length of the Kepler right triangle:

The shortest edge length of the Kepler right triangle is 12.

If the hypotenuse of a Kepler right triangle is divided by the measure for the shortest edge length of the Kepler right triangle the result is the Golden ratio of cosine (36) multiplied by 2 = Phi = 1.618033988749895.

The shortest edge length of the Kepler right triangle is 12. 12 multiplied by the Golden ratio of cosine (36) multiplied by 2 = Phi = 1.618033988749895 = 19.41640786499874.

The hypotenuse of a Kepler right triangle that has its shortest edge length equal to 12 is equal to 19.41640786499874.

Apply the Pythagorean theorem to the hypotenuse of the Kepler right triangle and the shortest edge length of the Kepler right triangle to get the measure for the second longest edge length of the Kepler right triangle.

19.41640786499874 squared = 376.996894379984929.

12 squared = 144.

376.996894379984929 subtract 144 = 232.996894379984929.

The square root of 232.996894379984929 = 15.26423579416883.

The second longest edge length of the Kepler right triangle that has its shortest edge length equal to 12 is equal to 15.26423579416883.

15.26423579416883 divided by 4 = 3.816058948542208 the diameter of the circle.

15.26423579416883 divided by the square root of the Golden ratio = 1.272019649514069 = 12. 12 is the measure for both the circumference of the circle and the shortest edge length of the Kepler right triangle that has its hypotenuse equal to 19.41640786499874 while the second longest edge length of the Kepler right triangle is equal to 15.26423579416883.

Circumference of circle and the shortest edge length of the mentioned Kepler right triangle are both equal to 12.

1 quarter of the second longest edge length of the Kepler right triangle and the diameter of the circle are both equal to 3.816058948542208.

12 divided by 3.816058948542208 = Pi = 3.144605511029692.

Slimzie Maygen - 2 years, 11 months ago

Pi can also be calculated from a square and a circle with the same surface area because if the edge of a square is multiplied by √√φ = 1.127838485561682 then the result is the diameter of a circle with the same surface area as the square and if the perimeter of a square is divided by √√φ = 1.127838485561682 the result is the circumference of a circle with the same surface area as the square. Circumference of circle divided by diameter of circle = π = 3.144605511029693144.

Also you do NOT need Pi to create a circle and a square with the same surface area instead you MUST use √√φ = 1.127838485561682: http://www.wolframalpha.com/input/?i=√√φ

The creation of a circle and a square with the same surface area can also be used to find Pi

If only the surface area for a circle is known and the desire is to know both the measure of the circumference and the diameter of the circle a solution for finding the measure for the diameter of the circle is to multiply the square root for the surface area by the ratio 1.127838485561682. To find the measure for the circumference of a circle when only the surface area of a circle is known a solution is to multiply the square root of the circle's surface area by 4 then divide the result of multiplying the square root of the circle's surface area by 4 by the ratio 1.127838485561682.Please remember that the ratio 1.127838485561682 is the square root of the ratio 1.272019649514069 and the ratio 1.272019649514069 is the square root of the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.

If only the surface area for a circle is known and the desire is to know both the measure of the circumference and the diameter of the circle a solution for finding the measure for the diameter of the circle and the circumference of the circle is to divide the square root for the surface area of the circle by the ratio 1.127838485561682 resulting in quarter of the circle’s circumference. If 1 quarter of a circle’s circumference is multiplied by the square root of the Golden ratio = 1.272019649514069 the result is the diameter for the circle. Please remember that the ratio 1.127838485561682 is the square root of the ratio 1.272019649514069 and the ratio 1.272019649514069 is the square root of the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.

For example.

The edge of square is equal to 3.383515456685047.

3.383515456685047 divided by 3 = √√φ = 1.127838485561682.

3.383515456685047 multiplied by √√φ = 1.127838485561682 =

3.816058948542207 the diameter of a circle with the same surface area as the square with a width equal to 3.383515456685047.

3.383515456685047 multiplied by 4 = 13.534061826740188 the perimeter of the square.

13.534061826740188 divided by √√φ = 1.127838485561682 = 12 the circumference of a circle with the same surface area as the square with a width equal to 3.383515456685047.

12 divided by 3.816058948542207 = Pi = 3.144605511029693.

Quadrature of the circle constants again:

The Golden ratio Phi = Cosine (36) multiplied by 2 = 1.618033988749895.

The square root of Phi = 1.272019649514069.

1.272019649514069 squared = 1.618033988749895.

The square root of the square root of Phi = 1.127838485561682.

1.127838485561682 squared = 1.272019649514069.

The true value of Pi = 4 divided by 1.272019649514069 = 3.144605511029693144.

The square root of Pi = 2 divided by 1.127838485561682 = 1.773303558624324.

2 divided by the square root of Golden Pi = 1.773303558624324 = 1.127838485561682.Please remember that the ratio 1.127838485561682 is the square root of the ratio

1.272019649514069 and the ratio 1.272019649514069 is the square root of the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.

1.773303558624324 squared = 3.144605511029693144.

Slimzie Maygen - 2 years, 11 months ago

The ratio for the diameter of a circle divided by 1 quarter of the circle's circumference is the square root of the Golden ratio = 1.2720196495141 because if I divide the circumference of a circle into 12 equal parts and places 3 chords from the circle's circumference that has been divided into 12 at any of the 2 poles for the circle's diameter on a horizontal straight line perpendicular to the vertical diameter of the circle I will get a Kepler right triangle with the diameter of the Kepler right triangle as the second longest edge length of the Kepler right triangle while the shortest edge length of the Kepler right triangle is equal in measure to 1 quarter of the circle's circumference.

To prove that if the diameter of a circle is divided by 1 quarter of the circle’s circumference then the resulting ratio is the square root of the Golden ratio = 1.27201964951406. Also to prove that if the radius of a circle is divided by one 8th of the circle’s circumference then the resulting ratio is the square root of the Golden ratio = 1.27201964951406:

Method 1: Construct 2 perfect right angles that are perpendicular to each other. The vertical right angle can be used as the diameter of a circle that has its circumference divided into 12 equal parts. The horizontal right angle can be used for placing 1 quarter of the circle’s circumference on a straight line. Remember that 12 divided by 4 is 3 and if one 12th of a circle’s circumference is multiplied 3 equal times on a straight line the resulting measure is 1 quarter of the circle’s circumference. Multiply the measure for the diameter of the circle by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 so that the result is a line that has been divided into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895. The longer part of the line divided into the Golden ratio of Cosine (36) multiplied by 2 = 1.61803398874989 is the diameter of a circle. The whole line that was divided into the Golden ratio of Cosine (36) multiplied by 2 = 1.61803398874989 is the diameter of a semi-circle. If the circumference of the semi-circle touches the further end of the measure that is equal to 1 quarter of the circle’s circumference that was placed upon the horizontal straight line then it is proven that if the diameter of a circle is divided by 1 quarter of a circle’s circumference the resulting ratio is the square root of the Golden ratio = 1.27201964951406.

Method 2: Create a circle with a circumference 100% equal in measure to the perimeter of a square by ensuring that half the width of the square is equal to one 8th of the circle’s circumference. Both the circle and the square must share the same centre in this example. Add the edge of a decagon to the radius of the circle from the centre of the circle that shares the same radius as the circle. A decagon is a 10-sided polygon. If the radius of a decagon is divided by the edge of a decagon then the resulting ratio is the Golden ratio of Cosine (36) multiplied by 2 = 1.61803398874989. The combined measures of the radius of the circle plus the edge of a decagon with a radius equal in measure to the radius of the circle must then be used as the measure for the diameter of a semi-circle that has been divided into the Golden ratio of Cosine (36) multiplied by 2 = 1.61803398874989, with the radius of the circle being the larger part of the of the semi-circle being divided into the Golden ratio of Cosine (36) multiplied by 2 = 1.61803398874989. If the semi-circle that has a diameter that is made from the combined measures of the radius of the larger circle and the edge of a decagon with a radius equal in measure to the radius of the larger circle touches the further edge of half the width of the square that has a perimeter equal in measure to the circumference of the larger circle then it will be proven that if the radius of a circle is divided by one 8th of a circle’s circumference then the resulting ratio the square root of the Golden ratio = 1.27201964951406. : https://archive.is/ZSTzZ Show less

Slimzie Maygen - 2 years, 11 months ago

The knowledge of the ratio of the diameter of the circle divided by 1 quarter of the circle's circumference being equal to the square root of the Golden ratio = 1.272019649514069 is ancient knowledge and can be traced back to the approximation of 14 divided by 11 = 1.272727272727273 that comes from 4 divided by Pi as 22 divided by 7 = 3.142857142857143. 14 divided by 11 = 1.272727272727273 is used by some geometricians to create a circle with a circumference that is equal in measure to the perimeter of a square:

Diameter of circle = 14.

Circumference of circle = 44.

Perimeter of square = 44.

14 divided by the square root of 154 = 1.128152149635532 is an approximation of the √√φ = 1.127838485561682. 14 divided by the square root of 154 = 1.128152149635532 is the square root of 14 divided by 11 = 1.272727272727273. 14 divided by the square root of 154 = 1.128152149635532 is also used by me and some geometricians to create a circle and a square with the same surface area according to Pi as 22 divided by 7 = 3.142857142857143:

Area of circle = 154.

Diameter of circle = 14.

Circumference of circle = 44.

Ancient Egyptian Pi = 22 divided by 7 = 3.142857142857143.

12 squared = 144. 3 squared = 9. 1 squared = 1

144 + 9 + 1 = 154.

The knowledge of the square root of the Golden ratio being applicable to the diameter of a circle divided by 1 quarter of the circle's circumference can easily be verified if 2 right angles are created and the vertical right angle is used for the diameter of the circle while the horizontal right angle has 1 quarter of the circle's circumference placed on to it resulting in a Kepler right triangle with the diameter of the circle being the second longest edge length of the Kepler right triangle while the shortest edge length for the Kepler right triangle is equal in measure to 1 quarter of the circle's circumference.

The fact that the result of creating 2 perfect right angles with the vertical right angle being used as the diameter of the circle while the horizontal right angle is used as 1 quarter of the circle's circumference results in a Kepler right triangle is 100% proof that the real value of Pi = 4/√φ = 3.144605511029693144.

Apply the Pythagorean theorem to al the edges of the Kepler right triangle to get the exact measure for the diameter of the circle then divide the circumference of the circle by the diameter of the circle to get Pi = 4/√φ = 3.144605511029693144.

The Kepler right triangle is also featured in the Great Pyramid of Giza and also the Earth and moon ratio according to Pi as 22 divided by 7 = 3.142857142857143.

Kepler right triangle: https://www.goldennumber.net/triangles/

Method for constructing a Kepler right triangle: https://en.wikipedia.org/wiki/File:KeplerTriangleConstruction.svg

Kepler right triangle in the Great Pyramid of Giza: https://houseoftruth.education/en/teaching/mona-lisa/theorem-5-kepler-triangle-in-the-great-pyramid Pyramid and Squaring the circle: http://www.dailymotion.com/video/xijbpvpyramid-and-squaring-the-circletech?GKFACEBOOKOG_HTML5=1

The square root for the square of the Golden ratio = sqrt[sqrt(phi)] √√φ = 1.127838485561682 is the key to creating a circle and a square with the same surface area: http://www.wolframalpha.com/input/?i=√√φ

Slimzie Maygen - 2 years, 11 months ago

PI IS NOT NEEDED FOR ANYTHING THERE ARE ALTERNATIVES TO PI LIKE THE SQUARE ROOT OF THE GOLDEN RATIO = 1.272019649514069 THAT REVEALS THE TRUE VALUE OF PI = 4/√φ = 3.144605511029693144.

A circle’s circumference can be divided into 12 equal parts with the use of just compass and straight edge and stylus after the circumference of the circle has fist been divided into 4 equal parts by using the 2 opposing diameters of the circle as bases for 2 equilateral triangles. After the circumference of the circle has been divided into 4 equal parts the next step is to multiply the radius of the circle upon the circle’s circumference from all 4 of the cardinal points of the circle’s circumference resulting in the division of the circle’s circumference into 12 equal parts.

AFTER THE CIRCLE’S CIRCUMFERENCE HAS BEEN DIVIDED INTO 12 EQUAL PARTS WITH 12 EQUAL CHORDS AROUND THE CIRCLE'S CIRCUMFERENCE WITH A COMPASS AND STRAIGHT EDGE THEN COMMON SENSE SHOULD TELL THE GEOMETER THAT 1 QUARTER OF THE CIRCE'S CIRCUMFERENCE IS EQUAL TO 3 BECAUSE 12 DIVIDED BY 4 = 3.

HOW TO CONSTRUCT A CIRCLE WITH 1 QUARTER OF THE CIRCLE'S CIRCUMFERENCE BEING PLACED ON A STRAIGHT LINE NEXT TO ANY OF THE 2 POLES FOR THE CIRCLE’S VERTICAL DIAMETER WITH OUT DIVIDING THE CIRCLE’S CIRCUMFERENCE INTO EQUAL PARTS.

IF THE DIAMETER OF THE CIRCLE IS THE LONGER MEASURE OF A LINE THAT HAS BEEN DIVIDED INTO THE GOLDEN RATIO OF COSINE (36) MULTIPLIED BY 2 = Phi = 1.618033988749895 THEN THE DISTANCE BETWEEN THE END OF THE MEASURE THAT IS EQUAL TO 1 QUARTER OF THE CIRCLE'S CIRCUMFERENCE THAT HAS BEEN PLACED ON A STRAIGHT LINE NEXT TO ANY OF THE 2 POLES FOR THE VERTICAL DIAMETER OF THE CIRCLE AND THE END OF THE LINE THAT WAS DIVIDED INTO THE GOLDEN RATIO OF COSINE (36) MULTIPLIED BY 2 = Phi = 1.618033988749895 WITH THE DIAMETER OF THE CIRCLE AS THE LONGER MEASURE IS EQUAL TO THE DIAMETER OF THE CIRCLE AND THE HYPOTENUSE OF A KEPLER RIGHT TRIANGLE THAT HAS ITS SECOND LONGEST EDGE LENGTH EQUAL TO 1 QUARTER OF THE CIRCLE'S CIRCUMFERENCE.

NO NEED FOR PI JUST USE THE SQUARE ROOT OF THE GOLDEN RATIO = 1.272019649514069 INSTEAD: The square root of the square root of Phi = 1.272019649514069: http://www.wolframalpha.com/input/?i=%E2%88%9A%CF%86

PI ONLY COMES INTO EXISTENCE WHEN THE CIRCUMFERENCE OF THE CIRCLE IS DIVIDED BY THE DIAMETER OF THE CIRCLE OR WHEN WE MEASURE THE AMOUNT OF TIMES THE DIAMETER OF A CIRCLE CYLINDER WITH 1 METER DIAMETER FIT AROUND THE CIRCUMFERENCE OF THE CIRCLE CYLINDER. THE KEY TO FINDING THE TRUE VALUE OF PI GEOMETRICALLY IS TO FIRST KNOW THE RATIO FOR THE DIAMETER OF A CIRCLE DIVIDED BY 1 QUARTER OF THE CIRCLE’S CIRCUMFERENCE. THE RATIO FOR THE DIAMETER OF A CIRCLE DIVIDED BY 1 QUARTER OF THE CIRCLE’S CIRCUMFERENCE HAS BEEN PROVEN BY GEOMETRIC CONSTRUCTION OF A CIRCLE WITH A CIRCUMFERENCE THAT IS EQUAL IN MEASURE TO THE PERIMETER OF A SQUARE TO BE THE SQUARE ROOT OF THE GOLDEN RATIO = 1.272019649514069. Divide a Circle into 12 Equal Parts using a compass and a ruler: https://www.youtube.com/watch?v=VMOuFXWVULI

PI IS NOT NEEDED FOR ANYTHING INSTEAD A CIRCLE CAN BE CALCULATED USING THE SQUARE ROOT OF THE GOLDEN RATIO = 1.272019649514069: https://archive.is/ZSTzZ PI IS JUST 1 OF MANY UNIVERSAL CONSTANTS THAT HAS BEEN DERIVED FROM THE SQUARE ROOT OF THE GOLDEN RATIO = 1.272019649514069: http://measuringpisquaringphi.com/five-more-universal-constants/

Pyramid and Squaring the circle: http://www.dailymotion.com/video/xijbpvpyramid-and-squaring-the-circletech?GKFACEBOOKOG_HTML5=1

Slimzie Maygen - 2 years, 11 months ago

The true value of Pi = 3.144605511029 is NOT Transcendental:

Pi = 4/√φ = 4 divided by 1.2720196495141 = 3.144605511029. π = 4/√φ = 3.144605511029693144.

THE REAL VALUE OF Pi IS NOT TRANSCENDENTAL BECAUSE THE REAL VALUE OF PI = 4/√φ = 3.144605511029693144 IS THE ONLY VALUE OF PI THAT CAN FIT THE FOLLOWING POLYNOMIAL EQUATION: 4th dimensional equation/polynomial for Golden Pi = 3.144605511029693 (x4 + 16x2 – 256 = 0). https://www.tiger-algebra.com/drill/x~4-16x~2-256=0/

Wolfram Alpha proof that the real Pi is NOT transcendental:

• http://www.wolframalpha.com/input/?i=x4+%2B+16x2+–++256+%3D+0

• http://www.wolframalpha.com/input/?i=4%2F%E2%88%9A%CF%86

• Panagiotis Stefanides fourth order equation: http://www.stefanides.gr/Html/piquad.html

Slimzie Maygen - 2 years, 11 months ago

To get the correct measure for a circle’s diameter and to prove that Golden Pi = 4/√φ = 3.144605511029693144 is the true value of Pi by applying the Pythagorean theorem to all the edges of a Kepler right triangle when using the second longest edge length of a Kepler right triangle as the diameter of a circle then the shortest edge length of a Kepler right triangle is equal in measure to 1 quarter of a circle’s circumference. Also if the radius of a circle is used as the second longest edge length of a Kepler right triangle then the shortest edge length of a Kepler right triangle is equal to one 8th of a circle’s circumference:

Example 1: The circumference of the circle is 12 but the measure for the diameter of the circle is not yet known. The second longest edge length of a Kepler right triangle is used as the diameter of a circle in this example. 12 divided by 4 is 3 so the shortest edge length of the Kepler right triangle is 3. The hypotenuse of a Kepler right triangle divided by the shortest edge length of a Kepler right triangle produces the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895. According to the Pythagorean theorem the hypotenuse of any right triangle contains the sum of both the squares on the 2 other edges of the right triangle.

So the shortest edge length of the Kepler right triangle is 3 and since the ratio gained from dividing the hypotenuse of a Kepler right triangle by the measure for the shortest edge of the Kepler right triangle is the Golden ratio of Cosine (36) multiplied by 2 = 1.61803398874989 then the measure for the hypotenuse of a Kepler right triangle that has its shortest edge length as 3 is 4.854101966249685. 4.854101966249685 divided by 3 is the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895. The square root of the Golden ratio = 1.272019649514069

4.854101966249685 squared is 23.562305898749058.

3 squared is 9.

23.562305898749058 subtract 9 = 14.562305898749058

The square root of 14.562305898749058 is 3.816058948542208.

Remember that the second longest edge length of the Kepler right triangle is used as the diameter of a circle. So the measure for both the second longest edge length of this Kepler right triangle and the diameter of the circle is 3.816058948542208.

Remember that the shortest edge length of this Kepler right triangle is 3 and is equal to 1 quarter of a circle’s circumference that has a measure of 12 equal units.

Circumference of circle is 12

Diameter of circle is 3.816058948542208.

Diameter of circle is 3.816058948542208 divided by the square root of the Golden ratio = 1.272019649514069 = 3 the edge of the square.

3 multiplied by 4 = 12.

The perimeter of the square = 12.

12 divided by 3.816058948542208 = Golden Pi = 3.144605511029693144.

4/√φ = Pi = 3.144605511029693144 multiplied by the diameter of the circle = 3.816058948542208 = 12.

The circumference of the circle is the same measure as the perimeter of the square.

4/√φ = 3.144605511029693144 is the true value of Pi.

PYTHAGOREAN THEOREM: https://en.wikipedia.org/wiki/Pythagorean_theorem

Slimzie Maygen - 2 years, 11 months ago

Golden Pi = 4/√φ = 3.144605511029693144 is the correct value of Pi and this fact can be proven by almost anybody that has sufficient knowledge of the principles of the Kepler right triangle including the creation of a circle with a circumference equal in measure to the perimeter of a square.

The correct value of the Golden ratio will determine the correct value of both the square root of the Golden ratio and Pi.

Traditional Pi 3.141592653589793 is also false because it is based upon a false value for the Golden ratio for example traditional Pi 3.141592653589793 can also be gained from 4 divided by the square root of 1.621138938277405 = 1.273239544735163. The ratio 1.621138938277405 can be gained in Trigonometry through the formula Cosine (35.84839254086685) multiplied by 2. The ratio 1.621138938277405 is a very poor approximation of the real Golden ratio of 1.618. The correct value for the Golden ratio is Cosine (36) multiplied by 2 = 1.618033988749895 and the correct value for the square root of the Golden ratio is 1.27201964951406. 16 divided by traditional Pi 3.141592653589793 squared = 9.869604401089357 results in the False value of the Golden ratio 1.621138938277405, while 16 divided by Golden Pi 3.144605511029693 squared = 9.888543819998317 = 1.618033988749895. Remember that 1.618033988749895 is the real Golden ratio and NOT 1.621138938277405. We do not even need to use any of the Pi values to determine the diameter of a circle or the circumference of a circle instead we can use the Square root of the Golden ratio = 1.27201964951406. If we multiply 1 quarter of the circle's circumference by 1.27201964951406 then the result is the correct measure for the circle's diameter. If we already know the length of the circle's diameter but we do not yet know the measure for the circle's circumference then all we have to do is divide the measure of the circle's diameter by 1.27201964951406 and the result will be 1 quarter of the circle's circumference. Multiply 1 quarter of the circle's circumference by 4 and obviously we have the value for the circumference of the circle. If we use 1.27201964951406 to get the length of the circle's diameter or the measure for the circle's circumference and then we divide the measure for the circle's circumference by the measure for the circle's diameter I guarantee you the result is 3.144605511029693.

The Kepler right triangle has so much wisdom encoded in it.

The Kepler right triangle is proof that 3.144605511029693 is the correct value for Pi.

3.141592653589793 as Pi has already been proven to be false by the aid of computer software that demonstrate that the curve of a circle can never be filled completely by polygons so the assumption that the gaps in the circle’s curve will disappear is false and thus proves that the multiple Polygon method for deriving a value of Pi is flawed because the multiple polygon method can only give us approximations for Pi while the Kepler right triangle gives us the exact value of Pi and that is 3.144605511029693. For example if the second longest edge length of a Kepler right triangle is the same length as the diameter of a circle then shortest edge length of the Kepler right triangle is equal to 1 quarter of the circle’s circumference. So if the shortest edge length of the Kepler right triangle is multiplied by 4 and the result divided by the second longest edge length while we use 1.27201964951406 then we can get the correct value of Pi and again that is 3.144605511029693. The Kepler right triangle is also the key to squaring the circle with equal perimeters and also equal areas. So almost anybody can get the right value of Pi by just constructing a Kepler right triangle and also a pocket calculator. Remember that the hypotenuse of a Kepler right triangle divided by the shortest edge length produces the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895, while the second longest edge length of a Kepler right triangle divided by the shortest edge length produces the square root of the Golden ratio 1.27201964951406.

Pi can be also be calculated from a Kepler right triangle if the measure for the perimeter of the square that is located on the shortest edge length of the Kepler right triangle is divided by the measure for the second longest edge length of the Kepler right triangle.

Pi can also be gained if the measure of the perimeter of the square that is located on the second longest edge length of a Kepler right triangle is divided by the hypotenuse of the Kepler right triangle. Traditional Pi = 3.141 can also be gained from a Kepler right triangle that has a hypotenuse with a measure of 34 while the shortest edge length of this Kepler right triangle is 21 and the second longest edge length of the Kepler right triangle has a measure that is equal to the square root of 715. 34 and 21 are both numbers that can be found among the Fibonacci sequence that progresses towards the Golden ratio Phi of Cosine (36) multiplied by 2 = 1.618033988749895 when any of the numbers that are next to each other in the Fibonacci sequence are divided by each other resulting in an approximation for the Golden ratio-Phi of Cosine (36) multiplied by 2 = 1.618033988749895. 34 divided by 21 = 1.619047619047619. 1.619047619047619 is an approximation for the Golden ratio –Phi of Cosine (36) multiplied by 2 = 1.618033988749895. 21 multiplied by 4 = 84. 84 divided by the square root of 715 = 3.141421886428416. 3.141421886428416 multiplied by the square root of 715 = 84. The real value of Pi = 3.144605511029… and can be gained from a Kepler right triangle that has a hypotenuse that has a measurement of 9227465, while the shortest edge length of this Kepler right triangle is 5702887 and the measurement for the second longest edge length of this Kepler right triangle is 7254184.322958371. 9227465 and 5702887 are numbers that are both featured among the Fibonacci sequence that moves towards the Golden ratio-Phi of Cosine (36) multiplied by 2 = 1.618033988749895 when any of the numbers that are next to each other in the Fibonacci sequence are divided by each other resulting in an approximation for the Golden ratio-Phi of Cosine (36) multiplied by 2 = 1.618033988749895. 9227465 divided by 5702887 = the Golden ratio-Phi of Cosine (36) multiplied by 2 = 1.618033988749895. 5702887 multiplied by 4 = 22811548. 22811548 divided by 7254184.322958371 = 3.144605511029681 multiplied by 7254184.322958371. = 22811548. 3.144605511029…….. is the true real value of Pi. Traditional Pi 3.141592653589793 has been proven to be Transcendental in addition to being irrational. Traditional Pi 3.141592653589793 is Transcendental because Traditional Pi 3.141592653589793 does not fit any polynomial equations. Squaring the circle with equal surface areas becomes possible and easy after traditional Pi 3.141592653589793 has been rejected and replaced with other values of Pi that are NOT transcendental. Golden Pi = 3.144605511029693 is irrational but Golden Pi is NOT transcendental because Golden Pi = 3.144605511029693 is the only value of Pi that fits the following polynomial equation: 4th dimensional equation/polynomial for Golden Pi = 3.144605511029693. (x4 + 16x2 – 256 = 0). (https://www.tiger-algebra.com/drill/x~4-16x~2-256=0/) Wolfram Alpha proof that the real Pi is NOT transcendental

• Wolfram Alpha proof that the real Pi is NOT transcendental http://www.wolframalpha.com/input/?i=x4+%2B+16x2+–+256+%3D+0

• http://www.wolframalpha.com/input/?i=4%2F%E2%88%9A%CF%86

Kepler right triangle information:

https://houseoftruth.education/en/teaching/mona-lisa/theorem-5-kepler-triangle-in-the-great-pyramid

https://www.goldennumber.net/triangles/

https://en.wikipedia.org/wiki/File:KeplerTriangleConstruction.svg

The real value of Pi = 4/√φ on Facebook: https://m.facebook.com/TheRealNumberPi/

Website for the real value of pi = 4/√φ: www.measuringpisquaringphi.com

Download for free and keep and read The book of Phi volume 8: The true value of Pi = 3.144, by Mathematician and author Jain 108: https://lists.gnu.org/archive/html/help-octave/2016-07/pdf1s8_jmqrL6.pdf

Slimzie Maygen - 2 years, 11 months ago

Mathematical proof that a Kepler right triangle can be used to create a circle with a circumference equal in measure to the perimeter of a square:

The Golden ratio Phi = the square root of 5 Plus 1 divided by 2 = 1.618033988749895.

The Golden ratio in Trigonometry is also equal to cosine (36) multiplied by 2 = 1.618033988749895.

The ratio 1.272019649514069 is the square root of the Golden ratio Phi = 1.618033988749895. Circumference of circle is 8 times the square root of the Golden ratio = 1.272019649514069 = 10.176157196112552. The circumference of the mentioned circle is equal to 10.176157196112552 equal units of measure. The diameter of the circle is equal in measure to the square root of 5 = 2.23606797749979 plus 1 = 3.23606797749979. 10.176157196112552 divided by 3.23606797749979 = Golden Pi = 3.144605511029693. If Golden Pi is multiplied by the measure for the diameter of a circle the result is the measure for the circumference of the circle. Golden Pi = 3.144605511029693 multiplied by 3.23606797749979 = the measure for the circumference of a circle that is equal to 10.176157196112552 units of measure. If the diameter of a circle is divided by the square root of the Golden ratio = 1.272019649514069 the result is a measure that is equal to 1 quarter of the circle’s circumference. If the edge of a square is equal in measure to 1 quarter of a circle’s circumference then the perimeter of the square is equal in measure to the circumference of the circle. The diameter of the mentioned circle = 3.23606797749979 divided by the square root of the Golden ratio = 1.272019649514069 = 2.544039299028138. 2.544039299028138 is 1 quarter of the ratio 10.176157196112552.

The circumference of the circle is equal to 10.176157196112552 equal units of measure according to Golden Pi = 3.144605511029693. The perimeter of the square is equal also to 10.176157196112552 equal units of measure according to the square root of the Golden ratio = 1.272019649514069.

The diameter of the circle is also used as the second longest edge length of a Kepler right triangle while the shortest edge length of the Kepler right triangle is equal in measure to 1 quarter of the circle’s circumference. If the hypotenuse of the Kepler right triangle is divided by 1 quarter of the circle’s circumference the result is equal to the Golden ratio of cosine (36) multiplied by 2 = 1.618033988749895.

Slimzie Maygen - 2 years, 11 months ago

“Further information on using a Kepler right triangle to determine the correct value of Pi”: If a isosceles triangle that is made from 2 Kepler right triangles is inscribed inside of a circle then the 2 lengths of the isosceles triangle that emerge from the base of the isosceles triangle are both equal in measure to 1 quarter of the circle’s circumference and this information help to determine the exact length of a circle’s circumference in relation to a circle’s diameter.

  1. The hypotenuse of a Kepler right triangle divided by the shortest edge length of the Kepler right triangle produces the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.

  2. If the diameter of the circle is divided into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 then the longer measure of the division of the circle’s diameter divided into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 is equal to the second longest edge length of a Kepler right triangle that has its hypotenuse equal in length to 1 quarter of the circle’s circumference when the Kepler right triangle is created inside of the circle.

  3. The shorter measure of the circle’s diameter divided into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 is equal in measure to the shortest edge length of a Kepler right triangle that has its hypotenuse equal in measure to the longer measure for the division of this circle’s diameter into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895. So the height of the isosceles triangle that is made from 2 Kepler right triangles that is inscribed inside of this circle is equal in measure to the hypotenuse of a Kepler right triangle that has its second longest edge length equal in measure to half the base width of the isosceles triangle that is made from 2 Kepler right triangles that has been inscribed inside of this circle.

  4. So according to the Pythagorean theorem if 1 quarter of the circle’s circumference is squared and also 1 quarter of the circle’s circumference is divided by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 and the smaller measure of the circle’s circumference that is divided into the Golden ratio of Cosine (36) multiplied by 2 is squared and then subtracted from the square of 1 quarter of the circumference of the circle and the remainder is applied to square root then the result of all the equations can then be divided into the Golden ratio of Cosine ( 36 ) multiplied by 2 = 1.618033988749895 and the shorter measure of the remainder can be added to the remainder resulting in the exact measure for the diameter of the circle in relation to the circle’s circumference.

  5. If the shortest edge length of a Kepler right triangle is divided by the second longest edge length of a Kepler right triangle the result is the ratio 1 quarter of Pi = 0.786151377757423. Golden Pi = 3.144605511029694 divided by 4 = 0.786151377757423. 0.786151377757423 squared = the reciprocal of the Golden ratio = 0.618033988749895. The reciprocal of the Golden ratio = 0.618033988749895 can be gained through the formula Cosine (72) multiplied by 2 = 0.618033988749895. Always remember that if the second longest edge length of a Kepler right triangle is used as the diameter of a circle then the shortest edge length of a Kepler right triangle will be equal to 1 quarter of a circle’s circumference on a straight line.

(A) 1 quarter of the circle’s circumference divided by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.

(B) The result of dividing 1 quarter of the circle’s circumference into the Golden ratio of Cosine (36) multiplied by = 1.618033988749895 multiplied by the square root of 1.618033988749895 (1.27201964951406) results in the second longest edge length of a Kepler right triangle that is half of a isosceles triangle created inside of the circle that has its 2 slanted lengths equal to 1 quarter of the circle’s circumference.

(C) The height of the isosceles triangle that has its 2 slanted edge lengths equal to 1 quarter of the circle’s circumference divided into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 then the longer measure of the height of the isosceles triangle that has its 2 slanted lengths equal to 1 quarter of the circle’s circumference is divided into the Golden ratio of Cosine (36) by 2 = 1.618033988749895 is added to the second longest edge length of the Kepler right triangle that both equal to the height of this isosceles triangle and is half of this isosceles triangle resulting in the right measure for the diameter of the circle in relation to the circumference of the circle.

If the isosceles triangle that is inscribed inside of this circle is divided into 2 Kepler right triangles and only 1 of the Kepler right triangles that is half of the isosceles triangle has the Pythagorean theorem applied to it plus the second longest edge length of the Kepler right triangle that is half of the isosceles triangle that has been inscribed inside of this circle is divided by the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 and the shorter measure of the second longest length of the Kepler right triangle divided into the Golden ratio is added to the second longest edge length of the Kepler right triangle then the correct measure for the length of the circle’s diameter in relation to the circumference of the circle can be known. If the measure for the circumference of a circle is divided by the diameter of the circle the resulting ratio is Pi.

“How to determine the exact circumference of a circle when only the length of the circle’s diameter is known and also further knowledge on how to gain the correct value of Pi”:

  1. Divide the diameter of the circle into the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 and the shorter length of the circle’s diameter divided into the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 must then be divided by the square root of 1.618033988749895 (1.27201964951406).

  2. The result of the circle’s diameter divided into the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 and then be divided by the square root of 1.618033988749895 (1.27201964951406) must now be divided by Cosine (51.82729237298776) resulting in 1 quarter of the circle’s circumference.

Alternatively 1 quarter of a circle’s circumference can be known if only the diameter for circle is known by dividing the diameter of the circle into the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 and the shorter length of the circle’s diameter divided into the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 must then be squared according to the Pythagorean theorem. Also The result of the circle’s diameter divided into the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 and then be divided by the square root of 1.618033988749895 (1.27201964951406) must now be squared according to the Pythagorean theorem. The combination of both the greater length of the circle’s diameter being divided into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 and then the result of the greater length of the division of the circle’s diameter into the Golden ratio of Cosine (36) being divided by the square root of 1.618033988749895 (1.27201964951406) squared according to the Pythagorean theorem and then applied to square root can also reveal the measure for 1 quarter of the circle’s diameter when the circumference of the circle is not yet known and only the measure for the diameter of the circle is known.

  1. Now that the measure for 1 quarter of the circle’s circumference is known the measure for 1 quarter of the circle’s circumference must be multiplied by 4 and divided by the measure of the circle’s diameter that is already known before the circumference of the circle was known and the resulting ratio is the true value of Pi.

FURTHER DESCRIPTION OF DERIVING THE CORRECT VALUE OF PI WITH THE KEPLER RIGHT TRIANGLE:

  1. The hypotenuse of the right Kepler right triangle is equal to 1 quarter of the circle’s circumference in measure when an isosceles triangle that is made from 2 Kepler right triangles is created inside of a circle, but when the diameter of the circle is the same length of the second longest edge length of the Kepler right triangle then the shortest edge length of the Kepler right triangle becomes equal to 1 quarter of the circle’s circumference. If the second longest edge length of the Kepler right triangle is equal to the measure for the circle’s diameter and also the hypotenuse of the Kepler right triangle is divided into Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 then the larger part of the division will also be equal to 1 quarter of the circle’s circumference because if the hypotenuse of a Kepler right triangle is divided by the measure of the shortest edge length of a Kepler right triangle the result is the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 . If the hypotenuse of a Kepler right triangle is equal to length of a circle’s diameter then the second longest length of the Kepler right triangle is equal to 1 quarter of the circle’s circumference.

  2. Also the hypotenuse of the Kepler right triangle divided by the shortest edge length of the Kepler right triangle produces the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.

  3. The second longest edge length of a Kepler right triangle divided by the shortest edge length of the Kepler right triangle produces the ratio the square root of Phi 1.618033988749895 = 1.272019649514069.

  4. If you multiply the second longest edge length of a Kepler right triangle by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 then you will get the correct length for the diameter of a circle with a circumference four times larger than the measure for the length of the hypotenuse of the Kepler right triangle that is created inside the same circle.

  5. So if you already know the measure for the circumference of a circle but you do not yet know the correct length for the circle’s diameter a solution is to divide 1 quarter of the circle’s circumference by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 and then multiply the result of dividing 1 quarter of the circle’s circumference by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 by the ratio the square root of 1.618033988749895 (1.27201964951406) resulting in both the second longest edge length of a Kepler right triangle and also the larger measure of the circle’s diameter being divided into by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895. Remember that if you multiply the second longest edge length of a Kepler right triangle by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 the result is the correct length for the diameter of a circle with a circumference that is 4 times larger than the length of the hypotenuse of the Kepler right triangle that was used to determine the correct length of the circle’s diameter.

“More information on how to derive the correct value of Pi using a Kepler right triangle”:

The accuracy of the value of Pi that you get is determined by how accurate the value for the square root of the Golden ratio that you have. The accuracy for the value of the square root of the Golden ratio is determined by the accuracy of the Golden ratio that you have. All values of Pi are based on 4 divided by the square root of the Golden ratio.

• If the measure of the circumference of a circle is already known but the length of the circle’s diameter is not yet known another solution is to multiply 1 quarter of the circle’s circumference by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 and then apply the Pythagorean theorem to both 1 quarter of the circle’s circumference and also the result of multiplying 1 quarter of the circle’s circumference by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 with the diameter of the circle as the second longest edge length of the Kepler right triangle resulting in the measure for the diameter of the circle in this example. The same result for measure of the diameter of the circle can be gained if the result of multiplying 1 quarter of the circle’s circumference by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 is divided by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 and then 1 quarter of the circle’s circumference is multiplied by the square root of the Golden ratio = 1.618033988749895 = 1.272019649514069 resulting in the measure for the diameter of the circle.

• If the measure of the circumference of a circle is already known but the length of the circle’s diameter is not yet known another solution is to divide 1 quarter of the circle’s circumference by the square root of the Golden ratio = 1.618033988749895 = 1.272019649514069 and then apply the Pythagorean theorem to both 1 quarter of the circle’s circumference and also the result of dividing 1 quarter of the circle’s circumference by the square root of the Golden ratio = 1.618033988749895 = 1.272019649514069 with the diameter of the circle being the hypotenuse of the kepler right triangle resulting in the measure for the diameter of the circle in this example. The same result for measure of the diameter of the circle can be gained if the result of dividing 1 quarter of the circle’s circumference by the square root of the Golden ratio = 1.618033988749895 = 1.272019649514069 is multiplied by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 resulting in the measure for the diameter of the circle.

• If the measure of the circumference of a circle is already known but the length of the circle’s diameter is not yet known another solution is to divide 1 quarter of the circle’s circumference by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 and then apply the Pythagorean theorem to both 1 quarter of the circle’s circumference and also the result of dividing 1 quarter of the circle’s circumference by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 and then multiply the result of applying the Pythagorean theorem to both 1 quarter of the circle’s circumference and also the result of dividing 1 quarter of the circle’s circumference by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 resulting in the measure for the diameter of the circle . Remember that the hypotenuse of the Kepler right triangle is equal in measure to the edge of the square that is also equal in measure to 1 quarter of the circle’s circumference in this example. The same result for the measure of the diameter of the circle can be gained if 1 quarter of the circle’s circumference is divided by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 and then the result of dividing 1 quarter of the circle’s circumference by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 is multiplied by the square root of the Golden ratio = 1.618033988749895 = 1.272019649514069 and then multiply the measure that was multiplied by the square root of the Golden ratio = 1.618033988749895 = 1.272019649514069 by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 resulting in the measure for the diameter of the circle.

• If the measure of the circumference of a circle is already known but the length of the circle’s diameter is not yet known another solution is to multiply 1 quarter of the circle’s circumference by the square root of the Golden ratio = 1.618033988749895 = 1.272019649514069 and the result will be the correct length of the circle’s diameter. The length of a circle’s diameter can also be gained from by multiplying 1 quarter of the circle’s circumference by Tangent 51.82729237298776 degrees in Trigonometry. If the circumference of a circle is divided by the diameter of a circle the resulting ratio is Pi.

• If the measure of the circumference of a circle is already known but the length of the circle’s diameter is not yet known another solution is to multiply the circle’s circumference by the square root of the Golden ratio = 1.618033988749895 = 1.272019649514069 and remember that 1 quarter of the result of multiplying the circle’s circumference by the square root of the Golden ratio = 1.618033988749895 = 1.272019649514069 is the measure for the diameter of the circle.

• If the measure of the circumference of a circle is already known but the length of the circle’s diameter is not yet known and the desire is to know the length of the circle’s diameter another solution is to apply the Pythagorean theorem to both the measure of the circumference of the circle and also to the result of multiplying the measure for the circumference of the circle by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 and then divide the result of applying the Pythagorean theorem to both the measure of the circumference of the circle and also the result of multiplying the measure for the circumference of the circle by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 by 4 resulting in the measure for the diameter of the circle. Please remember that the shortest edge length of the Kepler right triangle is equal in measure to the circumference of the circle in this example.

• The ratio Pi and the measure for the diameter of a circle can also be gained by using the ratio the ratio 1.049346046019552 The ratio 1.049346046019552 is the square root of the ratio 1.024375930027425. The ratio 1.49346046019552 applies to the diagonal of a Golden Pi = 3.144605511029693 rectangle divided by the second longest edge length of a Golden Pi rectangle. If a right triangle is created that produces the ratio Golden Pi = 3.144605511029693 when the second longest edge length of the right triangle is divided by the shortest edge length of the right triangle then the result of dividing the measure for the hypotenuse of the right triangle by the second longest edge length of the right triangle is the ratio 1.049346046019552. The ratio 1.049346046019552 can be gained also if the square root of 17.618033988749895 is divided by 4. Please remember that the ratio 17.618033988749895 is equal to the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 plus 16. The ratio 1.049346046019552 can also be gained if the ratio 3.299779359290302 is divided by Golden Pi = 3.144605511029693.

If the measure of the circumference of a circle is already known but the measure of the circle’s diameter is not yet known and the desire is to know the measure for the diameter of the circle another solution is to multiply the circle’s circumference by the ratio 1.049346046019552 and then apply the Pythagorean theorem to both the result of multiplying the circumference of the circle by the ratio 1.049346046019552 and the circumference of the circle with the result of multiplying the circumference of the circle by the ratio 1.049346046019552 as the hypotenuse of the right triangle. Divide the measure for the circumference of the circle by the diameter of the circle to get the ratio Pi.

• If the measure of the diameter of a circle is already known but the measure of the circle’s circumference is not yet known and the desire to know the measure for the circumference of the circle another solution is to divide the circle’s diameter by the square root of 1.618033988749895 = 1.272019649514069 and the result will be 1 quarter of the circle’s circumference. Multiply 1 quarter of the circle’s circumference by 4 and the result is the measure for the circumference of the circle.

• If the measure of the diameter of a circle is already known but the measure of the circle’s circumference is not yet known and the desire is to know the measure for the circumference of the circle another solution is to multiply the circle’s diameter by 4 and then divide the result of multiplying the diameter of the circle by 4 by the square root of 1.618033988749895 = 1.272019649514069 and the result will be the measure for the circumference of a circle. Please remember that if the shortest edge length of a Kepler right triangle is divided by 1 quarter of the second longest edge length of the Kepler right triangle the result is Pi the ratio of a circle’s circumference divided by a circle’s diameter.

• If the measure of the diameter of a circle is already known but the measure of the circle’s circumference is not yet known and the desire is to know the measure for the circumference of the circle another solution is to multiply the circle’s diameter by 4 and then multiply the result of multiplying the diameter of the circle by 4 by the square root of 1.618033988749895 = 1.272019649514069. Next apply the Pythagorean theorem to both the result of multiplying the diameter of the circle by 4 and also the result of the diameter of the circle being multiplied by 4 and the square root of 1.618033988749895 = 1.272019649514069 resulting in the measure for the circumference of the circle. Please remember that if the hypotenuse of a Kepler right triangle is divided by the measure for the second longest edge length of a Kepler right triangle the result is the square root of 1.618033988749895 = 1.272019649514069.

• If the measure of the diameter of a circle is already known but the measure of the circle’s circumference is not yet known and the desire is to know the measure for the circumference of the circle another solution is to divide the diameter of the circle by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 and then apply the Pythagorean theorem to both the diameter of the circle and the result of dividing the diameter of the circle by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 with the diameter of the circle being the hypotenuse of a Kepler right triangle resulting in the second longest edge length of the Kepler right triangle that is also equal in measure to 1 quarter of the circle’s circumference .If a Kepler right triangle is created that has a hypotenuse that is equal in measure to the diameter of a circle then the shortest edge length of the Kepler right triangle that has a hypotenuse that is equal in measure to the diameter of a circle is the result of the diameter of the circle being divided by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895. If a Kepler right triangle is created that has a hypotenuse that is equal in measure to the diameter of a circle then the second longest edge length of the Kepler right triangle that has a hypotenuse that is equal in measure to the diameter of a circle is equal in measure to 1 quarter of the circle’s circumference.

• The ratio Pi and the measure for the circumference of a circle can also be gained by using the ratio the ratio 3.299779359290302. The ratio 3.299779359290302 is the square root of the ratio 10.888543819998315. The ratio 3.299779359290302 applies to the diagonal of a Golden Pi = 3.144605511029693 rectangle divided by the shorter edge length of a Golden Pi rectangle. If a right triangle is created that produces the ratio Golden Pi = 3.144605511029693 when the second longest edge length of the right triangle is divided by the shortest edge length of the right triangle then the result of dividing the measure for the hypotenuse of the right triangle by the shortest edge length of the right triangle is the ratio 3.299779359290302. The ratio 3.299779359290302 can be gained also if the square root of 17.618033988749895 is divided by the square root of the Golden ratio = 1.272019649514069. Please remember that the ratio 17.618033988749895 is equal to the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 plus 16. The ratio 3.299779359290302 can also be gained if the result of adding Golden Pi squared = 9.888543819998317 plus 1 squared is applied to square root according to the Pythagorean theorem. If the longer measure for a Golden Pi = 3.144605511029693 rectangle is 4 then the shorter measure for the Golden Pi = 3.144605511029693 rectangle is equal to the square root of the Golden ratio = 1.272019649514069,while the measure for the diagonal of the Golden Pi = 3.144605511029693 rectangle is equal to the square root of 17.618033988749895. Please remember again that the ratio 17.618033988749895 is equal to the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 plus 16. If the measure of the diameter of a circle is already known but the measure of the circle’s circumference is not yet known and the desire is to know the measure for the circumference of the circle another solution is to multiply the circle’s diameter by the ratio 3.299779359290302 and then apply the Pythagorean theorem to both the result of multiplying the diameter of the circle by the ratio 3.299779359290302 and the diameter of the circle with the result of multiplying the diameter of the circle by the ratio 3.299779359290302 as the hypotenuse of the right triangle. Divide the measure for the circumference of the circle by the diameter of the circle to get the ratio Pi.

Slimzie Maygen - 2 years, 11 months ago

How to derive the measure for the edge of a square that has the same surface area as a circle from calculating the surface area of the circle with a Kepler right triangle representing the square root of the Golden ratio = 1.272019649514069 and deriving the square root for the surface area of the circle:

If the measure for the surface area of a square with a width that is equal in measure to 1 quarter of the circumference of a circle is used as the shortest edge length of a Kepler right triangle then the second longest edge length of the Kepler right triangle is equal to the surface area of the mentioned circle. The second longest edge length of a Kepler right triangle is equal in measure to the surface area of a circle that has 1 quarter of its circumference equal in measure to the square root for the surface area that is located on the shortest edge length of the Kepler right triangle that has its second longest edge length being equal in measure to the surface area of the mentioned circle.

Remember that the second longest edge length of a Kepler right triangle is equal in measure to the surface area of a circle that has 1 quarter of its circumference equal in measure to the square root for the surface area that is located on the shortest edge length of the Kepler right triangle, thus the square root for the surface area of the mentioned circle can be gained by using the second longest edge length of the Kepler right triangle that is equal in measure to the surface area of the mentioned circle that has 1 quarter of its circumference equal in measure to the square root for the surface area that is located on the shortest edge length of the Kepler right triangle as the diameter of a semi-circle with the square root for the surface area of the circle being found between the first of the equal divisions of the surface area of the mentioned circle that have been placed on the second longest edge length of the Kepler right triangle from the end of the second longest edge length of the Kepler right triangle that is being used as the diameter of a semi-circle and the circumference of the semi-circle that has a diameter that is equal in measure to the second longest edge length of the Kepler right triangle.

Deriving the square root for the surface area of a circle is further confirmation for the creation of a circle and a square with the same surface area and remember that if a circle and a square have been created with the same surface area and the diameter of the circle is divided by the edge of the square the result is the square root of the Golden root 1.127838485561682. Also remember that if a circle and a square have been created with the same surface area and the radius of the circle is divided by half the measure for the edge of the square the result is also The square root of the Golden root 1.127838485561682. Please remember that the ratio 1.127838485561682 is the square root of the ratio 1.272019649514069 and the ratio 1.272019649514069 is the square root of the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.

“Creating a square with the same surface area as a circle from the mean proportional of a rectangle that has the same surface area as a rectangle that has its longer edge equal to half the circumference of the circle while its shorter edge is equal to the radius of the circle with the aid of a half of Golden Pi = 1.572302755514847 isosceles triangle that has a height equal to the diameter of the circle”:

  1. A circle and a rectangle and a isosceles triangle and a square with the same surface area can also be created if the mean proportional of a rectangle is used to create the width of the square and an isosceles triangle is created that has a height that is equal to the diameter of the circle while the base width of the isosceles triangle is equal to half the circumference of the circle, plus the longer edge of the rectangle is also equal to half the circumference of the circle while the shorter edge of the rectangle is equal to the radius of the circle.

  2. Create a circle and an isosceles triangle and make sure that the height of the isosceles triangle is equal in measure to the diameter of the circle while the base width of the isosceles triangle is equal in measure to half the circumference of the circle.

  3. Create a rectangle that has its longer edge equal to half the circumference of the circle and also the base width of the isosceles triangle that has its height equal to the diameter of the circle while the shorter edge of the rectangle must be equal to the radius of the circle and half the height of the mentioned isosceles triangle.

  4. Use the mentioned rectangle’s mean proportional to create a square that has the same surface area as the mentioned circle and the mentioned isosceles triangle and the mentioned rectangle. Remember that a circle with the same surface as a square can also be created if the diameter of the circle is the longer measure of a 1.127838485561682 ratio rectangle while the edge of the square is the shorter measure for a 1.127838485561682 ratio rectangle. Please remember that the ratio 1.127838485561682 is the square root of the ratio 1.272019649514069 and the ratio 1.272019649514069 is the square root of the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895. Compare the measure for the edge of the square that was created from the mentioned rectangle’s mean proportional to the edge of another square that also has the same surface area as the circle but was created by using the diameter of the circle plus 1 quarter of the circle’s circumference as the diameter of a semi-circle to discover that both of these squares are the same size.

“8 methods for finding the surface area of a circle”:

• Method 1 .The surface area of a circle can be known if the radius of a circle is squared and then multiplied by Pi.

• Method 2. The surface area of a circle can also be known if half the circumference of the circle is multiplied by the measure for the diameter of the circle and then the result of multiplying half the measure for the circumference of the circle must be divided into 2 resulting in the measure for the surface area of the circle. An isosceles triangle that is made from 2 Kepler right triangles has the same surface area as a circle that has a diameter that is equal in measure to the height of the isosceles triangle that is made from 2 Kepler right triangles. If half the circumference of a circle is divided by the diameter of the circle the result is the half of the ratio Pi.

• Method 3. The surface area of a circle can also be found if the radius of the circle is multiplied by half the circumference of the circle. If half the circumference of a circle is divided by the radius of a circle the result is the ratio Pi.

• Method 4. If the surface area of square that has a width equal in measure to 1 quarter of a circle’s circumference is multiplied by the square root of the Golden ratio = 1.272019649514069 the result is the surface area of the circle.

• Method 5. If the diameter of a circle is divided by the ratio 1.127838485561682 the result is the edge of a square that has the same surface area as the circle. Please remember that the ratio 1.127838485561682 is the square root of the ratio 1.272019649514069 and the ratio 1.272019649514069 is the square root of the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.

• Method 6. If the surface area of a square that has a width that is equal in measure to the diameter of a circle is divided by the square root of the Golden ratio = 1.272019649514069 the result is the surface area of the circle.

• Method 7. If the surface area of a square that has a diagonal that is equal in measure to the diameter of a circle is multiplied by half of Pi = 1.572302755514847 the result is the surface area of the circle.

• Method 8. If the surface area of a square that has a diagonal that is equal in measure to the diameter of a circle is divided by half the square root of the Golden ratio = 0.636009824757035 the result is the surface area of the circle.

• Draw Triangle with Same Area as Rectangle: https://www.youtube.com/watch?v=hOVuy_Z2BLY&t=39s

• Convert a triangle to a rectangle of equal area: https://www.youtube.com/watch?v=v1HwSEE5BaY

• Converting a triangle to a rectangle of equal area: https://www.youtube.com/watch?v=qmkzWkic1jw

• To construct a square of equal area to a rectangle using the mean proportional: https://www.youtube.com/watch?v=iRPK8Kh2VUY&t=49s

• Converting rectangle to a square of equal area: https://www.youtube.com/watch?v=WB74RFm_QUc

• Constructing a rectangle into a square with equal area by using the mean proportional – 16182588: https://www.youtube.com/watch?v=Rd7BDY5DuaU

Slimzie Maygen - 2 years, 11 months ago

Another example that the circle can be squared:

Common sense should tell any mathematician that if a rectangle and a circle can have the same surface area then a square and a circle can also have the same surface area because the rectangle's mean proportional can be used to create a square with the same surface area as the rectangle and if the shorter edge of a rectangle is equal in measure to the radius of a circle while the longer edge of the rectangle is equal to half the circumference of the circle then the rectangle and the circle MUST have the same surface area and since we have already got a rectangle and a circle with the same surface area the next step is to use the rectangle's mean proportional to create a square with the same surface area as both the rectangle and the circle. It is so easy to understand that squaring the circle is easy to do and we do NOT need Pi to square the circle but still stupid mathematicians are claiming that the circle cannot be squared in 2018 when such a claim as the circle cannot be squared with compass and straight edge has been proven to be 100% FALSE. If the circumference of a circle is 12 then the diameter of the circle is 3.8160589485423 according to real value of Pi = 4/√φ = 3.1446055110296. 3.8160589485423 divided by 2 = the radius of the circle = 1.9080294742712. 1.9080294742712 squared = 3.6405764746876. 3.6405764746876 multiplied by the real value of Pi = 3.144605110296 = the surface area of the circle = 11.448176845627. The longer edge of the rectangle is 6 and the shorter edge of the rectangle is 1.9080294742712.The radius of a circle with a circumference of 12 again = 1.9080294742712. 1.9080294742712 multiplied by 6 = 11.448176845627. The edge of the square with the same surface area as a circle with a circumference of 12 is equal to 3.3835154566851. 3.3835154566851 divided by 3 = √√φ = 1.127838485561682. If a circle and a square are created with the same surface area and then the diameter of the circle is divided by the edge of the square the result is the √√φ = 1.127838485561682.

The following YouTube video also admits that if a circle and a rectangle have the same surface area then the longer edge of the rectangle is equal to half the circumference of the circle while the shorter edge of the rectangle is equal to the radius of the circle: Area of a circle, how to get the formula: https://www.youtube.com/watch?v=YokKp3pwVFc • Draw Triangle with Same Area as Rectangle: https://www.youtube.com/watch?v=hOVuy_Z2BLY&t=39s • Convert a triangle to a rectangle of equal area: https://www.youtube.com/watch?v=v1HwSEE5BaY

• Converting a triangle to a rectangle of equal area: https://www.youtube.com/watch?v=qmkzWkic1jw • To construct a square of equal area to a rectangle using the mean proportional: https://www.youtube.com/watch?v=iRPK8Kh2VUY&t=49s • Converting rectangle to a square of equal area: https://www.youtube.com/watch?v=WB74RFm_QUc

• Constructing a rectangle into a square with equal area by using the mean proportional – 16182588: https://www.youtube.com/watch?v=Rd7BDY5DuaU

Do NOT use Pi to square the circle instead Rectify the circle and square the circle to find Pi. Rectify the circle applies to the creation of a circle with a circumference that is equal in measure to the perimeter of a square while squaring the circle applies to the creation of a circle and a square with the same surface area. For equal perimeters use the √φ = 1.272019649514069. For equal areas use √√φ = 1.127838485561682. Pi = 4/√φ = 3.144605511029693144.

I previously thought that squaring the circle was impossible until I discovered the square root of the Golden ratio and the real value of Pi = 4/√φ = 3.144605511029693144. Please remember that the real value of Pi = 3.144605511029693144 is NOT Transcendental because only the real value of Pi = 4/√φ = 3.144605511029693144 can fit the following polynomial equation:

4th dimensional equation/polynomial for Golden Pi = 3.144605511029693 (x4 + 16x2 – 256 = 0). https://www.tiger-algebra.com/drill/x~4-16x~2-256=0/

Wolfram Alpha proof that the real Pi is NOT transcendental: • http://www.wolframalpha.com/input/?i=x4+%2B+16x2+–+256+%3D+0

• http://www.wolframalpha.com/input/?i=4%2F%E2%88%9A%CF%86

√√φ = 1.127838485561682 is the key to creating a circle and a square with the same surface area. The following Wolfram alpha site gives us information about the ratio √√φ = 1.127838485561682 = http://www.wolframalpha.com/input/?i=√√φ

Slimzie Maygen - 2 years, 11 months ago

Another Quadrature of the circle example:

Phi = Cosine (36) multiplied by 2 = 1.618033988749895.

The square root of Phi = 1.272019649514069.

1.272019649514069 squared = 1.618033988749895.

The square root of the square root of Phi = 1.127838485561682.

1.127838485561682 squared = 1.272019649514069.

The true value of Pi = 4 divided by 1.272019649514069 = 3.144605511029693144.

The square root of Pi = 2 divided by 1.127838485561682 = 1.773303558624324.

1.773303558624324 squared = 3.144605511029693144.

• The quadrature of the circle example: The square root of the Golden ratio also called the Golden root = 1.272019649514069. The Golden root 1.272019649514069 is the result of either the diameter of a circle being divided by 1 quarter of a circle’s circumference or the radius of a circle being divided by one 8th of a circle’s circumference. The square root of the Golden ratio = 1.272019649514069 also applies to the perimeter of a square divided by the circumference of a circle with a diameter equal to the width of the square. The square root of the Golden ratio = 1.272019649514069 also applies to the surface area of a square divided by the surface area of a circle with a diameter equal to the width of the square. The square root of the Golden ratio = 1.272019649514069 also applies to the surface area of a square divided by the surface area of a circle with a circumference equal in measure to the perimeter of the square. The second longest edge length of a Kepler right triangle divided by the shortest edge length of a Kepler right triangle is the square root of the Golden ratio also called the Golden root = 1.272019649514069. The hypotenuse of a Kepler right triangle divided by the second longest edge length of a Kepler right triangle is the square root of the Golden ratio = 1.272019649514069.The square root of the Golden ratio = 1.272019649514069 can also be gained if the surface area of circle is multiplied by 16 and then the result of the surface area of a circle being multiplied by 16 is then divided by the circumference of the circle squared. If the measure for the diameter of a circle is multiplied by 4 and the result of multiplying the measure of a circle’s diameter by 4 is divided by the measure for the circumference of a circle the result is also the square root of the Golden ratio also called the Golden root = 1.272019649514069. 4 divided by Golden Pi = 3.144605511029693 = the square root of the Golden ratio = 1.272019649514069.The square root of the Golden ratio = 1.272019649514069 also applies to the calculation of the surface area of a circle when the surface area of a square with a width that is equal to 1 quarter of the circle’s circumference is multiplied by the square root of the Golden ratio = 1.272019649514069. If the surface area of a circle is multiplied by the square root of the Golden ratio = 1.272019649514069 the result is the square root for the diameter of the circle

• The square root of the Golden root = 1.127838485561682. The square root of the Golden root 1.127838485561682 can be gained if the diameter of a circle that has the same surface area as a square is divided by the width of the square that has the same surface area as the circle. The square root of the Golden root 1.127838485561682 can also be gained if the radius of a circle that has the same surface area as a square is divided by half the width of the square that has the same surface area as the circle. The square root of the Golden root 1.127838485561682 can also be gained if a circle and a square with the same surface area are created and the perimeter of the square is divided by the circumference of the circle. The second longest edge length of a Illumien right triangle divided by the shortest edge length of a Illumien right triangle is the ratio The square root of the Golden root = 1.127838485561682.If a circle and a square are created with equal areas of measure and the width of the square of the square is divided by the ratio 1.127838485561682 the result is equal to 1 quarter of the circle’s circumference that has the same surface area as the square and if 1 quarter of the circle’s circumference is multiplied by the ratio 1.272019649514069 the result is the measure for the diameter of the circle . If the width of the square is multiplied by the ratio 1.127838485561682 the result is the measure for the diameter of the circle with the same surface area as the square.

If a circle and a square are created with equal areas of measure and half the width of the square of the square is divided by the ratio 1.127838485561682 the result is equal to 1 eighth of the circle’s circumference that has the same surface area as the square and if 1 eighth of the circle’s circumference is multiplied by the ratio 1.272019649514069 the result is the measure for the radius of the circle. If half the width of the square is multiplied by the ratio 1.127838485561682 the result is the measure for the radius of the circle with the same surface area as the square.

If a circle and a square have been created with the circumference of the circle being equal in measure to the perimeter of the square and the desire is to gain the measure for the radius or the diameter of a circle that has the same surface area to the already existing square that already has a circle with a circumference that is equal to the perimeter of the square a solution is to divide the radius or the diameter of the circle that has a circumference equal to the perimeter of the square by the square root of the square root of Phi = 1.127838485561682 resulting in the measure for the radius or diameter of the circle that has the same surface area to the already existing square that has a perimeter that is equal in measure to the circumference of the already existing circle. Alternatively If a circle and a square have been created with the circumference of the circle being equal in measure to the perimeter of the square and the desire is to gain the measure for the edge of a square that has the same surface area as the already existing circle that has a circumference equal in measure to the perimeter of the already existing square a solution is to divide the radius or the diameter of the circle that has a circumference equal to the perimeter of the already existing square by the square root of the square root of Phi = 1.127838485561682 resulting in the measure for half the edge of the square or the edge of the square that has the same surface area as the already existing circle that has a circumference that is equal in measure to the perimeter of the already existing square. 2 divided by the square root of Golden Pi = 1.773303558624324 = 1.127838485561682.Please remember that the ratio 1.127838485561682 is the square root of the ratio 1.272019649514069 and the ratio 1.272019649514069 is the square root of the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.

• The surface area of a circle can be calculated if the diameter of a circle is divided by the Square root of Phi = 1.272019649514069 resulting in 1 quarter of the circle’s circumference and then half the circumference of the circle is then multiplied by the measure for the diameter of the circle and then the result of multiplying half the circumference of the circle by the measure for the diameter of the circle is divided in 2 resulting in the measure for the surface area of the circle.

Circumference of circle = the true value of Pi = 3.144605511029695

Diameter of circle = 1 Surface area of a circle with a diameter of 1 = 0.786151377757423

Edge of square = 0.886651779312162

0.886651779312162 squared = 0.786151377757423.

The square root of the square root of Phi = 1.272019649514069: http://www.wolframalpha.com/input/?i=%E2%88%9A%CF%86

The square root of the square root of Phi = 1.127838485561682 computed by Wolfram Alpha: http://www.wolframalpha.com/input/?i=√√φ

Slimzie Maygen - 2 years, 11 months ago

Explaining the causes of the quadrature of the circle.

First regarding the creation of a circle and a square with equal perimeters meaning the circumference of the circle is equal in measure to the perimeter of the square, the width of the square must be equal to 1 quarter of the circle’s circumference resulting in the perimeter of the square being the same measure as the circumference of the circle. For example if the circumference of the circle is 8 then the edge of the square with a perimeter that is equal to a circle with a circumference of 8 must be 2. Also if the square and circle share the same centre and the circumference of the circle is equal to the perimeter of the square then the radius of the circle must be the longer measure of a 1.272019649514069 ratio rectangle while half the central width of the square must be the shorter measure of a 1.272019649514069 ratio rectangle. If a circle and square are created with the perimeter of the square being the same measure as the circumference of the circle and the circle and square do NOT share the same centre then the diameter of the circle CAN be the longer measure of a 1.272019649514069 ratio rectangle while the edge of the square CAN be the shorter measure of a 1.272019649514069 ratio rectangle but this is NOT compulsory.

In another example the edge of the square is the longer measure of a 1.272019649514069 ratio rectangle while the shorter measure of the 1.272019649514069 ratio rectangle is equal in measure to 1 quarter of the real value of Pi = 3.144605511029693.

Second regarding the creation of a circle and a square with equal areas the radius of the circle must be the longer measure of a 1.127838485561682 ratio rectangle while half the central width of the square must the shorter measure of a 1.127838485561682 ratio rectangle if the circle and square share the same centre. If the circle and square do NOT share the same centre and the circle and square have the same surface area then the diameter of the circle CAN be the longer measure of 1.127838485561682 ratio rectangle while the edge of the square CAN be the shorter measure of a 1.12783848556 ratio rectangle but this is NOT compulsory.

The relationship between the circle and the square having the same perimeter or the same area is a result of 2 ratios that are related to the Golden ratio of cosine (36) multiplied by 2 = 1.618033988749895 being used and those 2 ratios again are:

• The square root of the Golden ratio also called the Golden root = 1.272019649514069. The Golden root 1.272019649514069 is the result of either the diameter of a circle being divided by 1 quarter of a circle’s circumference or the radius of a circle being divided by one 8th of a circle’s circumference. The square root of the Golden ratio = 1.272019649514069 also applies to the perimeter of a square divided by the circumference of a circle with a diameter equal to the width of the square. The square root of the Golden ratio = 1.272019649514069 also applies to the surface area of a square divided by the surface area of a circle with a diameter equal to the width of the square. The square root of the Golden ratio = 1.272019649514069 also applies to the surface area of a square divided by the surface area of a circle with a circumference equal in measure to the perimeter of the square. The second longest edge length of a Kepler right triangle divided by the shortest edge length of a Kepler right triangle is the square root of the Golden ratio also called the Golden root = 1.272019649514069. The hypotenuse of a Kepler right triangle divided by the second longest edge length of a Kepler right triangle is the square root of the Golden ratio = 1.272019649514069.The square root of the Golden ratio = 1.272019649514069 can also be gained if the surface area of circle is multiplied by 16 and then the result of the surface area of a circle being multiplied by 16 is then divided by the circumference of the circle squared. If the measure for the diameter of a circle is multiplied by 4 and the result of multiplying the measure of a circle’s diameter by 4 is divided by the measure for the circumference of a circle the result is also the square root of the Golden ratio also called the Golden root = 1.272019649514069. 4 divided by Golden Pi = 3.144605511029693 = the square root of the Golden ratio = 1.272019649514069.The square root of the Golden ratio = 1.272019649514069 also applies to the calculation of the surface area of a circle when the surface area of a square with a width that is equal to 1 quarter of the circle’s circumference is multiplied by the square root of the Golden ratio = 1.272019649514069. If the surface area of a circle is multiplied by the square root of the Golden ratio = 1.272019649514069 the result is the square root for the diameter of the circle.

• The square root of the Golden root = 1.127838485561682. The square root of the Golden root 1.127838485561682 can be gained if the diameter of a circle that has the same surface area as a square is divided by the width of the square that has the same surface area as the circle. The square root of the Golden root 1.127838485561682 can also be gained if the radius of a circle that has the same surface area as a square is divided by half the width of the square that has the same surface area as the circle. The square root of the Golden root 1.127838485561682 can also be gained if a circle and a square with the same surface area are created and the perimeter of the square is divided by the circumference of the circle. The second longest edge length of a Illumien right triangle divided by the shortest edge length of a Illumien right triangle is the ratio The square root of the Golden root = 1.127838485561682.If a circle and a square are created with equal areas of measure and the width of the square of the square is divided by the ratio 1.127838485561682 the result is equal to 1 quarter of the circle’s circumference that has the same surface area as the square and if 1 quarter of the circle’s circumference is multiplied by the ratio 1.272019649514069 the result is the measure for the diameter of the circle . If the width of the square is multiplied by the ratio 1.127838485561682 the result is the measure for the diameter of the circle with the same surface area as the square. If a circle and a square are created with equal areas of measure and half the width of the square of the square is divided by the ratio 1.127838485561682 the result is equal to 1 eighth of the circle’s circumference that has the same surface area as the square and if 1 eighth of the circle’s circumference is multiplied by the ratio 1.272019649514069 the result is the measure for the radius of the circle. If half the width of the square is multiplied by the ratio 1.127838485561682 the result is the measure for the radius of the circle with the same surface area as the square.

If a circle and a square have been created with the circumference of the circle being equal in measure to the perimeter of the square and the desire is to gain the measure for the radius or the diameter of a circle that has the same surface area to the already existing square that already has a circle with a circumference that is equal to the perimeter of the square a solution is to divide the radius or the diameter of the circle that has a circumference equal to the perimeter of the square by the square root of the square root of Phi = 1.127838485561682 resulting in the measure for the radius or diameter of the circle that has the same surface area to the already existing square that has a perimeter that is equal in measure to the circumference of the already existing circle.Alternatively If a circle and a square have been created with the circumference of the circle being equal in measure to the perimeter of the square and the desire is to gain the measure for the edge of a square that has the same surface area as the already existing circle that has a circumference equal in measure to the perimeter of the already existing square a solution is to divide the radius or the diameter of the circle that has a circumference equal to the perimeter of the already existing square by the square root of the square root of Phi = 1.127838485561682 resulting in the measure for half the edge of the square or the edge of the square that has the same surface area as the already existing circle that has a circumference that is equal in measure to the perimeter of the already existing square. 2 divided by the square root of Golden Pi = 1.773303558624324 = 1.127838485561682.Please remember that the ratio 1.127838485561682 is the square root of the ratio 1.272019649514069 and the ratio 1.272019649514069 is the square root of the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.

The square root of the square root of Phi = 1.272019649514069: http://www.wolframalpha.com/input/?i=%E2%88%9A%CF%86

The square root of the square root of Phi = 1.127838485561682 computed by Wolfram Alpha: http://www.wolframalpha.com/input/?i=√√φ

Slimzie Maygen - 2 years, 11 months ago
×

Problem Loading...

Note Loading...

Set Loading...