The Golden Ratio: What is it?

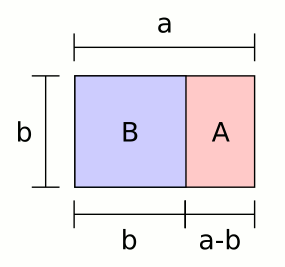
Consider the above picture (called the golden rectangle). There is a rectangle that when we separate it into a square and another rectanlge, the rectangle formed is similar to the original rectangle. Let $a$ be the longer side of the rectangle, and $b$ the shorter side. Then, because of the rectangles' similarity, we have the proportion:

$\frac{a}{b} = \frac{b}{a-b}$

We will name this value $\phi = \frac{a}{b}$ , the greek letter phi, and call it the Golden Ratio, just as the ancient Greeks did. At this point, this may just seem like some arbitrary geometrical figure. But $\phi$ has a lot of hidden properties, which we will uncover. First, let's try to find a numeric value for $\phi$ : Taking the reciprocal of both sides of the equation above gives

$\frac{b}{a} = \frac{a-b}{b} = \frac{a}{b} - 1$

or, by definition of $\phi$ ,

$\frac{1}{\phi} = \phi -1$ $\rightarrow 0 = \phi^2 - \phi - 1$ $\rightarrow \phi = \frac{1+\sqrt{5}}{2} \approx 1.618$

Now we know the actual value of the ratio of the sides of the rectangle first pictured above. The following forms of equations involving $\phi$ will be very useful to us in the future:

$\phi^2 = 1 + \phi$ $\phi = 1 + \frac{1}{\phi}$

You may be wondering right now why I took only the positive root when I applied the quadratic formula to find $\phi$ above. In the geometric sense, I wanted a ratio, and ratios are always positive. The negative root results in a negative value for $\phi$ . This value is called the conjugate of $\phi$ and has many similar properties to $\phi$ . But we will normally restrict ourselves to the positive value of $\phi$ . Tune in tomorrow for more mathematical information about the Golden Ratio.

Here is the next segment in the series.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

The Golden Ratio: What is it?

Comments