The Green Zone Problem

I'd like to bring your attention to this easy geometry problem that I call "The Green Zone Problem". Let's suppose there is an imaginary city in the Middle-earth. I call this imaginary city as Indigo City (feel free to give any cool name) and its shape is a triangle like the picture below: 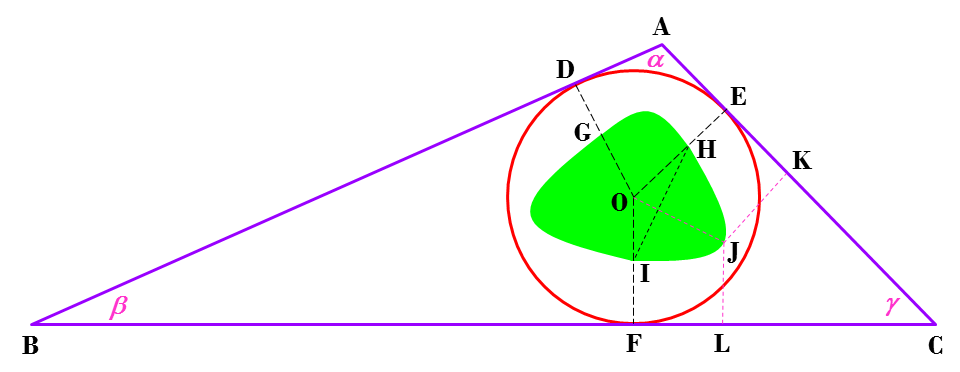The inscribed circle of the triangle is the incircle where the city council lives. The Green Zone is a city forest like Central Park in New York City. The interesting fact about the Green Zone is its boundary is always equidistant from the centre of circle and the closest triangle side, i.e. GO=DGGO=DG and JO=JK=JLJO=JK=JL but JO≠GOJO \neq GO. Using the conventional notations, we denote BC=aBC=a, AC=bAC=b, and AB=cAB=c. Just for the sake of fun, determine the area of the Green Zone in term of aa, bb, and cc.

Hint: If the shape of Indigo City is an equilateral triangle, unless I'm very much mistaken, then its area is 5a21083\dfrac{5a^2}{108}\sqrt{3}.

−ℏαρργ   ρrσβlϵm   sσlνιηg−\color{#3D99F6}{\Huge-\hbar\alpha\rho\rho\gamma\,\,\,\rho r\sigma \beta l\epsilon m\,\,\,s\sigma l\nu \iota\eta g-}

#Geometry

Note by Tunk-Fey Ariawan
5 years, 1 month ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

Ah, a nice way of introducing that wonderful property of X.

(Where X is to be determined by the reader)

Calvin Lin Staff - 5 years, 1 month ago

For an equilateral triangle, I'm getting 2327a2\displaystyle \frac{2\sqrt{3}}{27}a^2, with aa being the side of the triangle. The boundaries of the green zone are made up of parabolas right? Unless I did something wrong here, then I have a method to generalise this.

This is the solution I got for an equilateral triangle: https://www.desmos.com/calculator/ao5sksutzx

Julian Poon - 4 years, 6 months ago
×

Problem Loading...

Note Loading...

Set Loading...