The Infinite Atwood Machine

Consider the infinite Atwood’s machine shown in the figure.

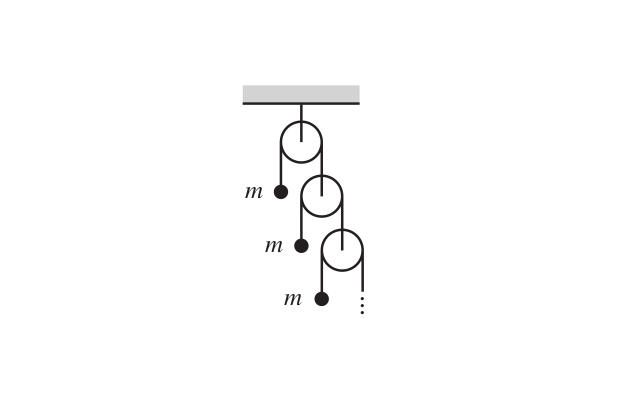
A string passes over each pulley, with one end attached to a mass and the other end attached to another pulley. All the masses are equal to m, and all the pulleys and strings are massless. The masses are held fixed and then simultaneously released. What is the acceleration of the top mass?

I have given the problem statement as it is. My humble request is for you all to help me obtain a mathematical solution to the above question rather than a trivial physical interpretation. Cheers!

#Mechanics

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Call the topmost block as $Block_0$ , the next block as $Block_1$ and so on.

Let $a_i$ denote the acceleration (in the downward direction) of $Block_i$ for $i=0,1,2 \ldots$ .

Then, by the principle of virtual work, we have: $\sum_{i=0}^{\infty} \frac{a_i}{2^i} = 0$

By Newton's second law, $mg - \frac{T}{2^i} = ma_i \quad i=0,1,2 \ldots$ Where $T$ is the tension in the string connecting $Block_0$ .

Now, plugging in the value of $a_i$ (from the second equation), into the first one, and some simplification, we get $T = \frac{3}{2} mg$

Hence, $\boxed{a_0=-\frac{g}{2}}$

A Former Brilliant Member - 5 years ago

Where can I read about principle of virtual work? Btw , very nice & smart sol.n !,+1! @Deeparaj Bhat

Rishabh Tiwari - 5 years ago

I think the general notion of conservation of string is termed as principle of virtual work by some other concept of energy conservation, maybe? Am I right @Deeparaj Bhat ?

Anirudh Chandramouli - 5 years ago

I believe in the latter. It is more commonly used than conplex words like "virtual work". Virtual work is nice but in real life it does not really apply because no machine is 100% efficient. Conservation of energy is better because it even covers dissipated energy.

Ashish Menon - 5 years ago

Actually, the principle of virtual work is far more general. In fact, it's in the heart of Lagrangian mechanics.

But, no, it's not really very related to energy conservation.

A Former Brilliant Member - 5 years ago

@A Former Brilliant Member – Yeah, but I have used the latter term often.

Ashish Menon - 5 years ago

@A Former Brilliant Member – yeah!! its more related to least action

i take it that u are invoking D'Alembert's form of the principle???

Rohith M.Athreya - 5 years ago

@Rohith M.Athreya – Yeah.

A Former Brilliant Member - 5 years ago

@Rohith M.Athreya – Why do you know lagrangian mechanics?:p

Anirudh Chandramouli - 5 years ago

@Anirudh Chandramouli – lol

i found this book by H.Goldstein in the basavangudi library which started with lagrangians and hamiltonian

Rohith M.Athreya - 5 years ago

@Rohith M.Athreya – Oh I'm reading that book as well. What a pleasant coincidence. Is it the one that starts with the mechanics of a single particle and then goes on to systems of particles and stuff?

Anirudh Chandramouli - 5 years ago

@Anirudh Chandramouli – That book was put in general by Julien in slack.

A Former Brilliant Member - 5 years ago

@A Former Brilliant Member – yes i know. that's how i got it...

Anirudh Chandramouli - 5 years ago

@Anirudh Chandramouli – Same here.

A Former Brilliant Member - 5 years ago

@Anirudh Chandramouli – yes :)

Rohith M.Athreya - 5 years ago

@A Former Brilliant Member – But isn't the basis for Lagrangian mechanics that Euler Lagrangian formula for energy or whatever. That is why I assumed that it had to do with energy

Anirudh Chandramouli - 5 years ago

@Anirudh Chandramouli – It more or less comes to that. But, it kicks off with virtual work. After a lot of simplification (and assumptions), you get the form that you're talking about.

A Former Brilliant Member - 5 years ago

@A Former Brilliant Member – ok thanks anyways. I am new to Lagrangian mechanics and hope I will master it soon. :)

Anirudh Chandramouli - 5 years ago

@A Former Brilliant Member – Are you all college guys!!

Faraz Khan - 5 years ago

@Faraz Khan – Nah I am in 11th :P

Ashish Menon - 5 years ago

@Faraz Khan – Just finished 12th :P

A Former Brilliant Member - 5 years ago

Hope so. @Swapnil Das , @Ashish Siva please comment.!

Rishabh Tiwari - 5 years ago

@Rishabh Tiwari – Yes both are there.

Ashish Menon - 5 years ago

Umm. Kind of a mixture of both.

Swapnil Das - 5 years ago

See this problem

Rishabh Tiwari - 5 years ago

I learnt from an old book of my dad's.

I don't know any good resource.

A Former Brilliant Member - 5 years ago

Can someone please provide a link to virtual work mechanics?

Rishabh Tiwari - 5 years ago

It is total work done is 0 in a fancy way

SUM Ti ai = 0

T sidharth - 3 years, 5 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$