The line through the feet of the bisectors

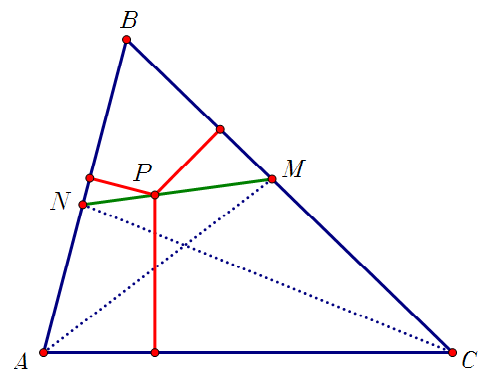
In the previous image $AM$ and $CN$ are bisectors and $P$ lies on the line segment $MN$ . Prove that the distance from $P$ to line $AC$ is equal to the sum of the distances from $P$ to lines $BA$ and $BC$ .
What happen if $P$ lies on the line $MN$ but outside the triangle?
Now draw the circumcircle of triangle $ABC$ and suppose the ray $MN$ intersects the circumcircle at $Q$ ( $N$ is between $Q$ and $M$ ). Prove that $\frac{1}{QA}=\frac{1}{QC}+\frac{1}{QB}$ .

#Geometry #Distance #Circumcircle #PeruMOTraining

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

I proved The first 1... and based on that created a problem. Maybe if u likeJorge,,,, you may share this problem. So here's the problem. In an acute angled triangle $ABC$ we have $BC=4$ , $AC=5$ , $AB=6$ . $BM$ and $CN$ are the internal bisectors of $B$ and $C$ . $P$ is any point on the segment $MN$ . If $[\triangle PMC]=1$ and $[\triangle PNB]=4$ , find $[\triangle BPC]$ . ( it wud be nice if u mention a little credit to me.. :P )

Sagnik Saha - 7 years, 4 months ago

Reply if you find this problem interesting! :)

Sagnik Saha - 7 years, 4 months ago

I think there are too many conditions in your problem. Triangle ABC is fixed and also the points M and N, thus if you choose P in line segment MN such that [BPN]=2 then [CPM] is determined and is not equal to 4. Another idea is to calculate [MNBC] and then find [BPC] (I think the answer will be different of yours).

Try this problem (using your notation):

If [BPN]=2, what is the correct value of [CMP]?

Jorge Tipe - 7 years, 4 months ago

Then cant we fix $P$ and say that suppose there exists a point $P$ on $MN$ such that ........ ?

Sagnik Saha - 7 years, 4 months ago

However, solution to #1. Let $PX \perp BC$ , $PY \perp AC$ and $PZ \perp AB$ . We drop $MM_1 \perp BC$ , $MZ_1 \perp AB$ and $NN_1 \perp BC$ and $NY_1 \perp AC$ . Now we have $\triangle BM_1M \cong \triangle BMZ_1$ (right angle, angle and side equal) and hence $MZ_1=MM_1$ . Similarly we have, $NN_1 = NY_1$ .

We use similarity in triangles $MPY$ and $MNY_1$ .

$\dfrac{PY}{NY_1} = \dfrac{MP}{NM}$ and we get $PY = \dfrac{PM}{NM} \times NY_1$ ...(i) Similarly we have $PZ = \dfrac{NP}{NM} \times MZ_1$ ...(ii)

Now, $NN_1 , PX,MM_1$ are 3 parallel lines . So we have $\dfrac{PM}{NM} = \dfrac{M_1X}{M_1N_1}$ .... (iii) We join $N, M_1$ and let that intersect $PX$ at $L$ .

Using $\triangle NLP \sim NM_1M$ , we have $\dfrac{PL}{MM_1} = \dfrac{NP}{NM}$ and thus $PL = \dfrac{NP}{NM} \times MM_1 = \dfrac{NP}{NM} \times MZ_1$ . (as $MM_1 = MZ_1$ ... (iv)

And, similarly using $\triangle M_1XL \sim \triangle M_1N_1N$ , we have

$LX = \dfrac{XM_1}{N_1M_1} \times NN_1 = \dfrac{PM}{NM} \times NY_1$ ...(v)

We observe that $(iv) + (v)$ is indeed $(i) + (ii)$ and Hence $PY + PZ = PL + LX = PX$

Sagnik Saha - 7 years, 4 months ago

Is it correct Jorge??

Sagnik Saha - 7 years, 4 months ago

It seems good, but you misplaced the points, for example you said $MM_1$ perpendicular to $BC$ .

Jorge Tipe - 7 years, 4 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$