This is what keeps me up at 2 o'clock in the morning

I want to write the formula that gives the area of a regular polygon with base $b$ and no. of angles $n$. See the figure I made [made on Paint Mircosoft]!

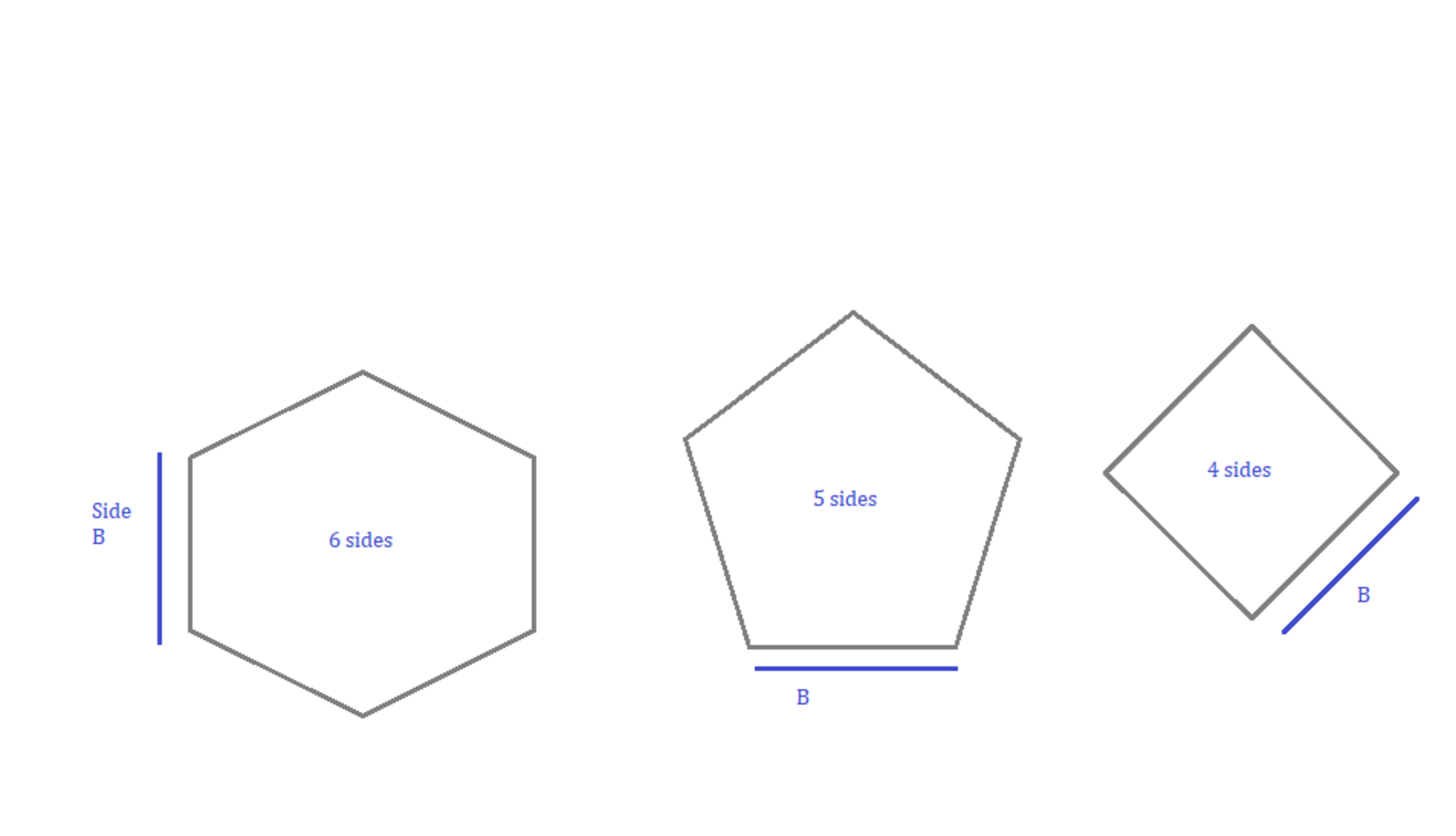
We can compose any polygon made of triangles, which always have 2 equal sides (Hexagon has 60-60-60 triangles, but it fits here), and the length of the triangle $l$ perpendicular to the base.

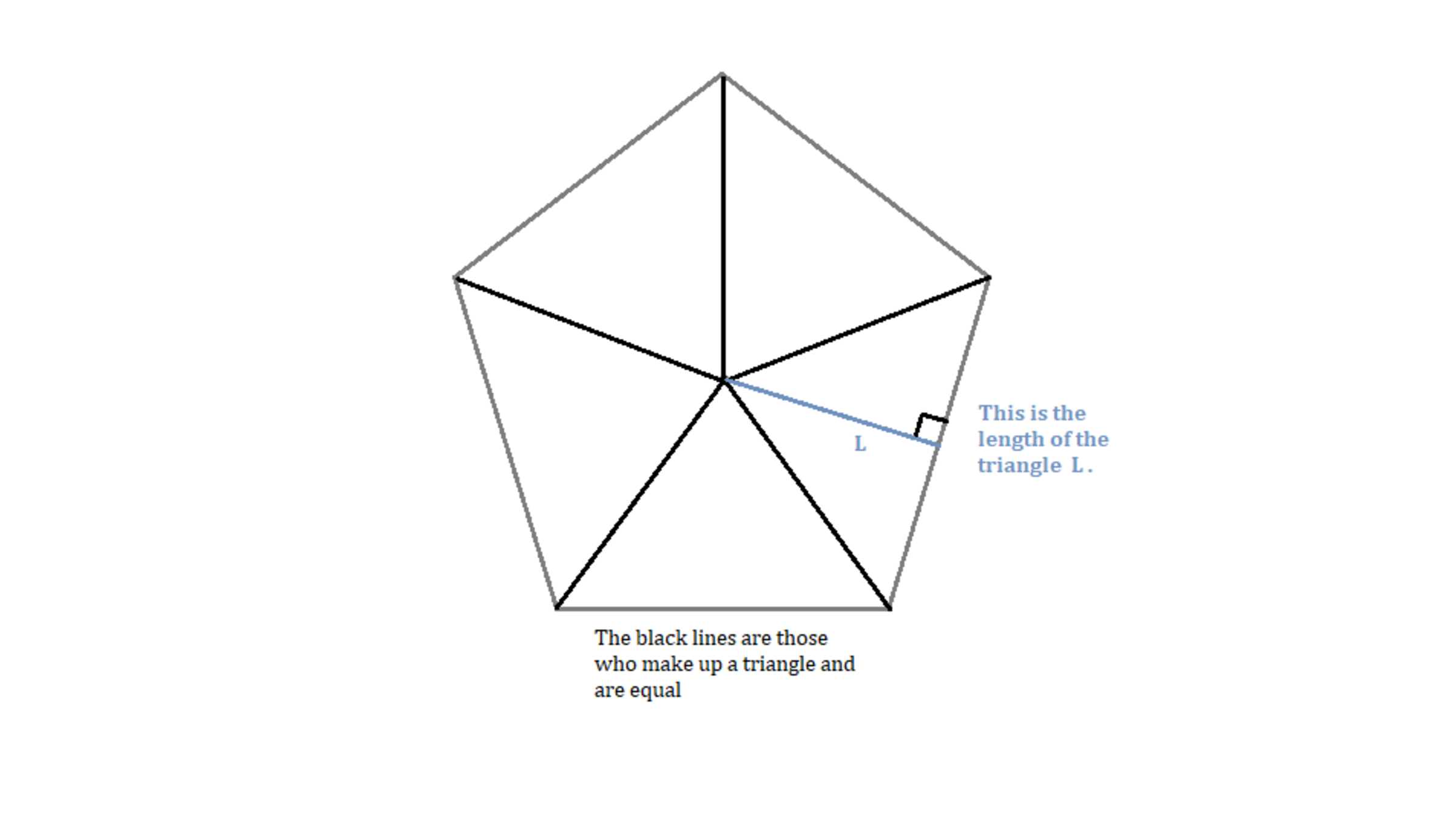
We can start to say that the area of the polygon is:

$S_{polygon} = \frac{ b \times l }{ 2 } \times n$ $\text{ "n" is the no. of triangles in the polygon}$

We can express $l$ with trigonometry:

• $\frac{ \tan \theta \times b }{ 2 } = l$

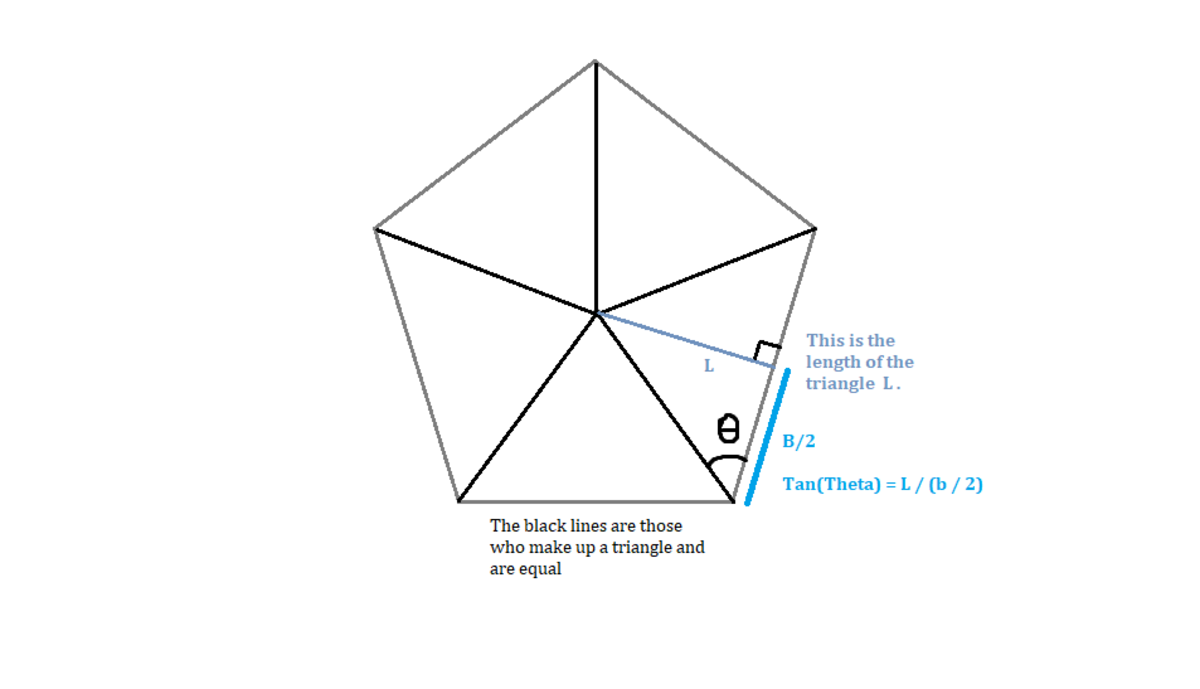
We replace this at the first formula:

• $S_{polygon} = \frac{ b \times \frac{ \tan \theta \times b }{ 2 } }{ 2 } \times n$
• $S_{polygon} = \frac{ b^2 \times \tan \theta \times n }{ 4 }$

How can we define $\theta$?

Remember that the sides of the regular polygon can be found using the formula $angle = \frac{(n - 2) \times 180 }{n}$, and for this case, it should be $\theta = \frac{(n - 2) \times 180 }{n \times 2}$, and, now we have the full formula:

$\boxed{ S_{polygon} = \frac{ b^2 \times \tan (\frac{(n - 2) \times 90 }{n}) \times n }{ 4 } }$

Please correct me for any mistake, typo or anything else against the guidelines. Ciao!