Three Kissing Circles

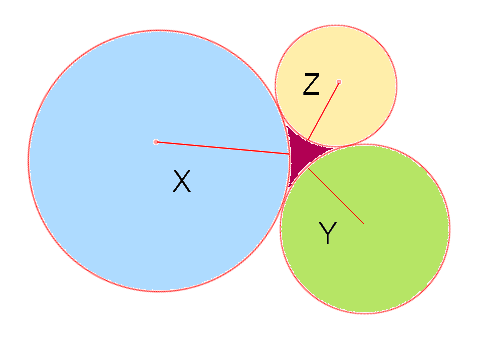
If three circles with radii \(x,y\), and \(z\) make tangents on each other as shown, what will be the area of the figure(magenta colored) formed between them in terms of \(x,y\), and \(z\)? I am posting my attempt below \(\frac { 1 }{ 2 } \left\{ \left( { x }^{ 2 }+xy+xz+yz \right) \ast \sin { \left( \cos ^{ -1 }{ \left( \frac { { x }^{ 2 }+xy+xz-yz }{ { x }^{ 2 }+xy+xz+yz } \right) } \right) } -\quad { x }^{ 2 }\cos ^{ -1 }{ \left( \frac { { x }^{ 2 }+xy+xz-yz }{ { x }^{ 2 }+xy+xz+yz } \right) -\quad { y }^{ 2 } } \cos ^{ -1 }{ \left( \frac { { y }^{ 2 }+xy+yz-xz }{ { y }^{ 2 }+xy+yz+xz } \right) -\quad { z }^{ 2 } } \cos ^{ -1 }{ \left( \frac { { z }^{ 2 }+xz+yz-xy }{ { z }^{ 2 }+xz+yz+xy } \right) } \right\} \)

#Geometry #AreaBetweenCurves #Circles

Note by Bilal Akmal
5 years, 10 months ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

Can you please elaborate on how you produced the formula.

Curtis Clement - 5 years, 10 months ago

Log in to reply

Form a triangle with the circles' origins as vertices.This should be equal to the magenta area plus some sectors of each circle. Minus the sectors and you get the above equation(angles assumed in radian.)

Bilal Akmal - 5 years, 10 months ago

Area of triangle - sum of the areas of three sectors

Vincent Miller Moral - 5 years, 10 months ago

Yeah, it works out fine. I get the same result, although not exactly with the same expression.

Michael Mendrin - 5 years, 10 months ago

"Update on the formula to calculate the magenta area": This one works too :)(angles are again assumed in radian) x2yz+xy2z+xyz2−x22[sin⁡−1(y+z2x+2y)+sin⁡−1(y+z2x+2z)]−y22[sin⁡−1(x+z2x+2y)+sin⁡−1(x+z2y+2z)]−z22[sin⁡−1(x+y2x+2z)+sin⁡−1(x+y2y+2z)]\sqrt { { x }^{ 2 }yz+x{ y }^{ 2 }z+xy{ z }^{ 2 } } -\frac { { x }^{ 2 } }{ 2 } \left[ \sin ^{ -1 }{ \left( \frac { y+z }{ 2x+2y } \right) } +\sin ^{ -1 }{ \left( \frac { y+z }{ 2x+2z } \right) } \right] -\frac { { y }^{ 2 } }{ 2 } \left[ \sin ^{ -1 }{ \left( \frac { x+z }{ 2x+2y } \right) +\sin ^{ -1 }{ \left( \frac { x+z }{ 2y+2z } \right) } } \right] -\frac { { z }^{ 2 } }{ 2 } \left[ \sin ^{ -1 }{ \left( \frac { x+y }{ 2x+2z } \right) +\sin ^{ -1 }{ \left( \frac { x+y }{ 2y+2z } \right) } } \right]

Bilal Akmal - 5 years, 10 months ago
×

Problem Loading...

Note Loading...

Set Loading...