Time Period of Vertical Circular motion

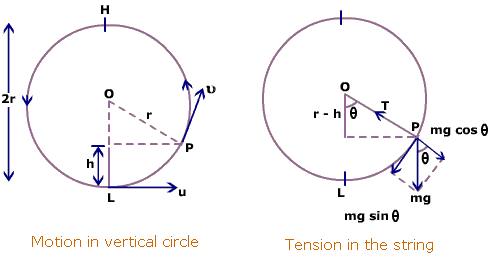
Note: $x$ has been used for the angle with the vertical, measured in anti-clockwise direction.

As shown in the figure, the tangential acceleration ${ a }_{ t }$ is $g\sin x$ . Thus, the angular acceleration will be $\frac { { a }_{ t } }{ R }$ , where $R$ is the radius of the circle. Writing $\frac { \omega d\omega }{ dx} =-\dfrac { g\sin x }{ R } int$ $\int _{ v/R }^{ \omega }{ \omega \, d\omega } =\dfrac { g\int _{ 0 }^{ x }{ \, sinx\, dx } }{ R } \\ { This\quad gives\\ \omega =\sqrt { \dfrac { 2g(1-\cos x) }{ R } +{ \dfrac { v }{ R } }^{ 2 } } =\dfrac { dx }{ dt } }$

Now, I don't know how to integrate this expression between $0\quad to\quad 2\pi$ , to calculate the time taken for complete oscillation.

So, please help by proceeding from here or if there is any other method to calculate the time period, please mention.

Thanks.

#Mechanics

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

There is no simple method to evaluate that integral.
Your equation is simply $\dfrac{d^2 \theta}{d t^2} + \dfrac{g \theta}{R} = 0$
The solution of this requires an elliptic integral to be solved.

Ameya Daigavane - 5 years, 2 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$