Tipped Over Cylinder

You have a cylinder with base B=πr² and height ℎ filled up to 𝑝 times the height (So if the cylinder were 2/3 full, p would be 2/3).

Now is the problem. The cylinder is tipped over. All havoc breaks loose.

Your task, as one of the most brilliant (no pun intended) people on Earth, is to find the height of the water from the bottom of the cylinder (So that the top water layer forms a chord on the cylinder's base and the new height is a line perpendicular to that chord dropped from the base's center).

Assume that the cylinder is not oblique and that this matter is of utter importance.

The problem may self-attribute clarity and maybe even simplicity with the implementation of labeled diagrams. I said that as a plural with good reason.

#Calculus

Note by Brennon Stevens
3 years ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

Hi Brennon, there is probably a much less complicated way than I've done it involving calculus, but from a purely geometrical route, here's what I found (although I probably made a calculation error somewhere:

Standing upright, Water Volume=πr2×p×h\text{Water Volume} = \pi r^2 \times p \times h

Label up the cylinder like shown below (where theta is in radians for ease of use):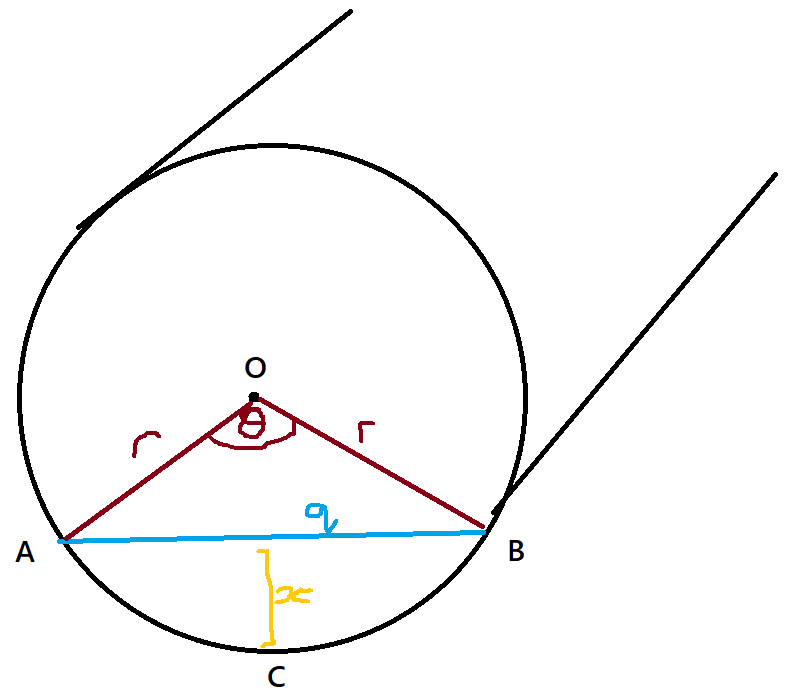

Sector Area OACB=θ2π×πr2\text{Sector Area OACB} = \frac{\theta}{2\pi} \times \pi r^2 Triangle Area OAB=12×r×r×sin⁡θ\text{Triangle Area OAB} = \frac12 \times r \times r \times \sin{\theta} Segment Volume ACB=(Sector Area OACB−TriangleAreaOAB)×h=hr22×(θ−sin⁡θ)\text{Segment Volume ACB} = (\text{Sector Area OACB} - {Triangle Area OAB}) \times h = \frac{hr^2}{2} \times (\theta - \sin{\theta})

Now equating the 2 volumes: πr2×p×h=hr22×(θ−sin⁡θ)\pi r^2 \times p \times h = \frac{hr^2}{2} \times (\theta - \sin{\theta}) θ−sin⁡θ=2π×p\boxed{\theta - \sin{\theta} = 2\pi \times p}

Applying the cosine rule to triangle OAB we get, q=2r2(1−cos⁡θ)q = \sqrt{2r^2(1 - \cos{\theta})}

Then by 1/2 * b * h, the area of the triangle is, 12×q×(r−x)\frac12 \times q \times (r-x) Equating this with the 1/2 * a * b * sinC version for the area found earlier, after some simplifying we get, r2∗sin⁡2θ=2(1−cosθ))(r−x)(r−x)r^2 * \sin^2{\theta} = 2(1 - cos{\theta}))(r - x)(r - x) Using sin^2 + cos^2 = 1, and simplifying to a quadratic in cos^2(theta): r2cos2θ−(2r2−4rx+2x2)cos⁡θ+(r2−4rx+2x2)=0r^2cos^2{\theta} - (2r^2 - 4rx + 2x^2)\cos{\theta} + (r^2 - 4rx + 2x^2) = 0 Using the quadratic formula we simplify this. If it is + used in the ±\pm then we get θ=0\theta = 0 so we need to use the -. This gives us, cos⁡θ=r2−4rx+2x2r2\cos{\theta} = \frac{r^2 - 4rx + 2x^2}{r^2}

Now if we put this into the boxed formula from above (and using the fact that sin(arccos(x)) = 1−x2\sqrt{1-x^2}), cos⁡−1(r2−4rx+2x2r2)−2(r−x)x(2r−x)r2=2π×p\cos^{-1}\big(\frac{r^2 - 4rx + 2x^2}{r^2}\big) - \frac{2(r-x)\sqrt{x(2r-x)}}{r^2} = 2\pi \times p

I can't see any further useful ways to simplify this (if this is indeed correct). However, you know the values of p and r, so using radians, it should be easy(ish) to find the value of x from this?

Stephen Mellor - 3 years ago
×

Problem Loading...

Note Loading...

Set Loading...