Tough geometry problem
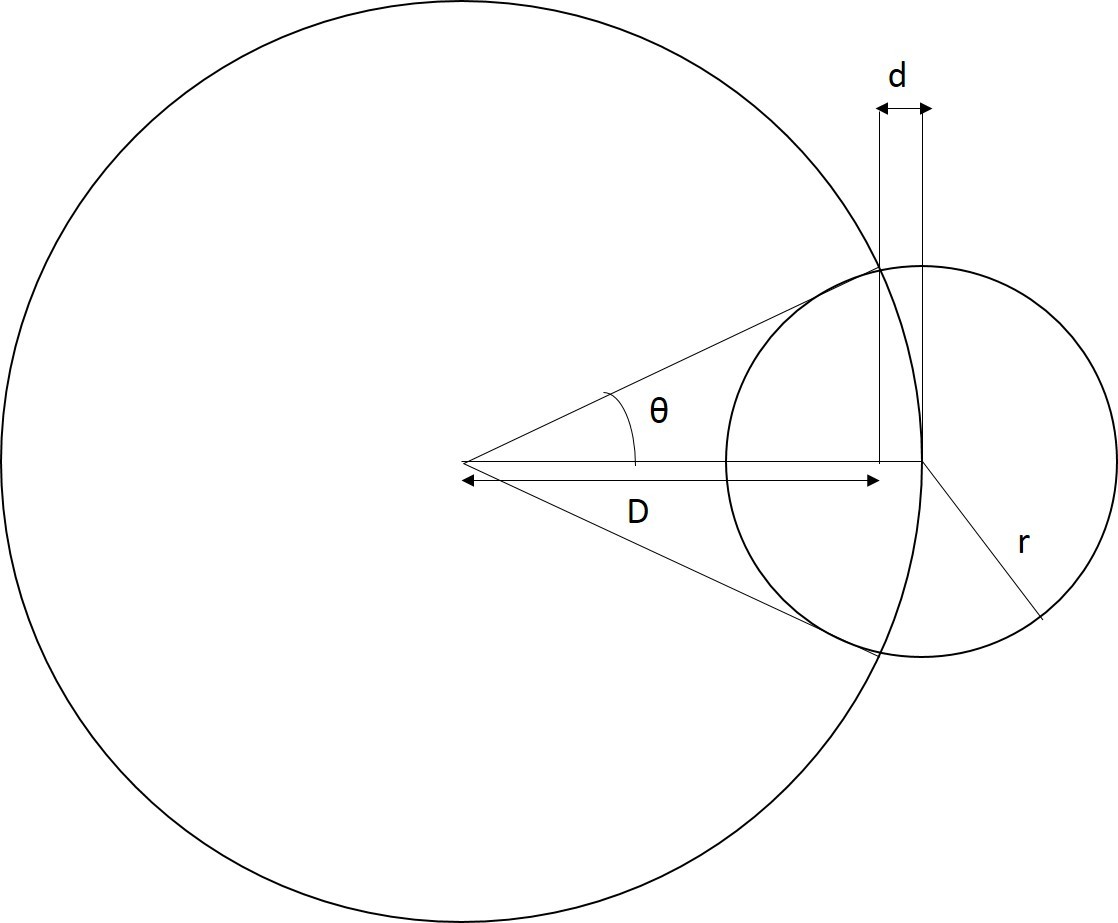
Hello can somebody help me find 'D' in terms of 'r' and 'd' please? I've been trying to get the answer for a while now but i end up with a really really complicated expression which i have a feeling isn't really right.. could use some help. Thanks in advance
No vote yet
16 votes
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
The radius of the LH circle is D+d. Consdering the isosceles triangle with angle θ and base r, we see that r=2(D+d)sin21θ The other two angles in this isosceles triangle are 90∘−21θ and so, looking at the small right-angled triangle on the right, sin21θ=cos(90∘−21θ)=rd Putting these results together we deduce that r2=2(D+d)d
Log in to reply
found this a different way a short while ago but thanks anyway :)
Log in to reply
You should post your solution!
Log in to reply
ah its here in one of the other comments :)
Nice and easy to understand.
Hi, This can be done using trigonometry
cos(θ)=D+dD --------- (1)
Joining the point of intersection of the two circles at the top to the center of the small circle, a beautiful triangle would be formed with,
sin(θ)=D+dr --------- (2)
Squaring and adding (1) and (2), we get
D2+r2=(D+d)2
Log in to reply
in case you're wondering how i got what i think is the right answer: cos theta=D/(D+d) as you found however when you make the other identity, if you use the cosine rule for non right angled triangles, you get that r=(D+d)sqrt(2(1-cos theta)), and so you just put the cos theta=D/(D+d) in from earlier and it rearranges pretty quickly to D=r^2/2d -d :)
Log in to reply
Thanks for pinning out the problem in my solution and thanks for giving the right solution.
I didn't follow you when you used the cosine rule. Please tell me, which triangle did you used to get it and how did you get r=(D+d)sqrt(2(1-cos theta)).
Log in to reply
ah well its the triangle where the three vertices are the centre of the large circle, the centre of the small circle, and one of the intersections of the two circles. if you use this triangle, its got both the large radii subtending the angle theta, and the far side (relative to theta) is the radius of the small circle. Here you can apply the formula c^2=b^2+a^2-2ab cos(C) for which I've found a clearer explanation here: http://drdjw.files.wordpress.com/2012/01/general-triangle.jpg
when you substitute them into that formula for the triangle we're using, you get that r=(D+d)sqrt(2(1-cos theta)), hope that helps :)
I think theres a problem with your sintheta = r/(D+d) . when you make that triangle, its an isosceles triangle not a right angled one even though it sort of looks like it should be a right angled one. however thanks anyway, your other identity i think has given me the clue and i think i've found the right answer anyway xD
Log in to reply
the radius meets the tangent at the circumference at right angles.
let the radius of the bigger circle be R.
let the perpendicular side of the right angle triangle be x. (having angle θ)
now, join the center of the smaller circle and the point of intersection between the smaller and bigger circle ( we have two point of intersections, but we will take the upper one), so now we have an another right angle triangle so, applying pythogorus theoram in our new right angle triangle :
x2+d2=r2
so, x2=r2−d2___ [1]
now coming back to our bigger right angle triangle
using pythogorus theoram again
we get
x2+D2=R2
putting value of x^{2} from eq. 1 and value of R (since R = D+d) we have
r2−d2+D2=(D+d)2
r2−d2+D2=D2+d2+2Dd
r2−2d2=2Dd
D=21dr2−2d2 ---- answer :)
(r^2)/2 = Dd + d^2
Is the line joining the centre of the bigger circle and the point of intersection of the two circles tangent to the second circle? Can it be proved?
Firstly we are assuming that the line that we can call R which is the radius of the larger circle is at a tangent to the perimeter of the smaller circle and a normal to the perimeter of the larger circle (only reason I mention this is because if you zoom on the picture this is perfectly correct) and lets call this point P. However assuming these, we can draw a triangle from the center of the small circle along the length D and then a 90° angle up to the point P which we call length x, hence the hypotenuse of this triangle is R. We can then make another triangle which starts from the center of the smaller triangle along the length d and then make another 90° angle up to the point P, the hypotenuse of this triangle is r. Further more, we know that R=D+d, using this information we can model a function of D(r,d):
Using Pythagoras's theorem:
R2=D2+x2
r2=d2+x2
Hence, when we cancel x:
R2−D2=r2−d2 where R=D+d
(D+d)2−D2=r2−d2
Which simplifies to, r2=2d(D+d)
Hence, D(r,d)=2dr2−d
wait, is D the radius of the larger circle???
Log in to reply
no, the radius of the larger circle is D+d
https://www.facebook.com/groups/572200892829750/ .... link of this solution check it out final relation is r=2 * (D+d) * Cos (theta/2)
This is solved easily using pythagoras famous equation. c2=a2+b2
the little triangle on the right tells us: r2=d2+h2
the left side triangle shares the same 'h' side, and we can also say that: (D+d)2=D2+h2
Substitute 'h' obtained from the first equation into the second one, and solve fo D in terms of d and r:
(D+d)2=D2+r2−d2
D2+2dD+d2=r2−d2+D2
D=(r2/2d)−d
Not so tough, but very fun.
r/tan@ -d
use trigonometry. tanθ=Dr
tanθ×D=r
or,
tan(90−θ)×r=D You have more than enough information in this problem.
Log in to reply
Thats in terms of theta as well. my problem is that i can't eliminate theta. btw the 'D' isn't the radius of the circle, but 'D+d' is
Fahad S. I don't think tan(theta)=r/d. join the radius of the smaller circle to the point of intersection of both the circles. you would find that the radius becomes the hypotenuse. hence the opposite side of the triangle containing theta is not equal to the radius.
Log in to reply
sorry, I had made one small mistake. It is D+dr
D = (r - d sin (teta) ) / (sin (teta) ) ????