The above constants c1,2,3,4 can be obtained by applying initial conditions.
Know that:
x(0)=y(0)=0
Integrating the velocities will give the displacements along each direction. It can be seen that as time increases, the particle eventually comes to rest. So the displacement when the particle comes to rest can be found as such:
xD=t→∞limx(t)yD=t→∞limy(t)
The required answer is, therefore:
D=xD2+yD2
I have not done all the calculations as doing so will take me time. I have laid out the steps to solve this problem.
Edit: I have solved for the particle's motion numerically with the following parameters:
B=q=m=u=1
The trajectory is plotted for various k as follows. One can see that when k=0 one gets the classical circular motion result. For the other cases, the motion is a stable spiral trajectory.
This discussion board is a place to discuss our Daily Challenges and the math and science
related to those challenges. Explanations are more than just a solution — they should
explain the steps and thinking strategies that you used to obtain the solution. Comments
should further the discussion of math and science.
When posting on Brilliant:
Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.
Markdown
Appears as
*italics* or _italics_
italics
**bold** or __bold__
bold
- bulleted - list
bulleted
list
1. numbered 2. list
numbered
list
Note: you must add a full line of space before and after lists for them to show up correctly
@Karan Chatrath acha to fir magnetic force aur drag force barabar ho jaayega to particle ruk jayega .
Right?, aisa aisa hua to bahut interesting ho jaayega
@Karan Chatrath if you don't mind,if it takes very much time. To write all thing in latex, which maybe a waste of time, then I suggest you to use pen and page.
@Karan Chatrath Yeah it worked finally.
The difference between your and my method is that , by your method we can find location of particle at any time t, and in my method I have just focused on where the particle stops.
Reply if you found it good.
@Lil Doug By the way, this is the same problem as the damping one you wanted me to solve, just with a little different final quantity to be solved for. Latex is being very buggy in the notes section, and I just lost a bunch of work trying to post the solution.
@Steven Chase I am not able to understand only that last line (velocity vector turns my 2π
Can you help me to understand that line.
Thanks in advance.
Hope I am not disturbing you.
The motion is described in terms of sinusoids of a certain frequency. You can find out what the time period is for the sinusoids, and evaluate the motion up until one time period has elapsed.
@Steven Chase
–
@Steven Chase sir i think the problem is whole same, except last line.
I have provided x(t) and y(t)
Can you do something from this data?
Thanks in advance.
Hope I am not disturbing you
I will try it, but I want to see your attempt before I post mine. Also, I posted a report on your problem titled 'Spaceship Mechanics'. Could you please get back to me on that?
@Karan Chatrath Yes sir, sorry I didn't reply you for that report.
The question is basically copied through the book, I checked it many times, there is nothing more than that given in question.
Can you please try to think it by seeing the graph.
@Krishna Karthik
–
@Krishna Karthik he is my favorite teacher.
He is just awesome bro.
Therefore I done that.
His skills of solving problem are better than even Einstein sir.
@Talulah Riley
–
What set Einstein apart was creativity, not problem-solving. But, both do go hand in hand in some way. He is quite remarkable, Karan Chatrath.
@Talulah Riley
–
Is my approach correct? Btw did you also start with this? Also, you can do this by linking using the work energy theorem (no differential equation solving there):
Ui=R−GMm
Uf=R0−GMm
501mv02−21mv02=Uf−Ui
You can get the exact same result with the above method.
@Krishna Karthik
–
@Krishna Karthik what is the meaning of “people there would struggle solving this problem.“
I don't think people of spacex will difficulty to solve that problem.
@Talulah Riley
–
Not really, but it's still super hard to do by pencil and paper. Besides, real rocket engineers probably haven't tried a problem under exam conditions in ages.
But this is a really tough one with lots of mathematically hard stuff. If you can somehow find Stephen Hawking in heaven and bring him back to Earth, he'll do it for you :)
@Krishna Karthik
–
@Krishna Karthik I agree.
Now I have some work, I am going, we will talk tomorrow regarding rocket problem .
By the way within 20min a new song of my favorite singer is coming, so I am very excited.
Bye.
@Karan Chatrath i have made necessary changes in the spaceship Mechanics.
Please delete the report.,
And within some hours I will post a note showing my attempt on that charge problem.
I thought the problem was telling us that 5t0 was the time it took for the velocity to drop to e−5v0. Like a "five time constant" thing. Which doesn't quite make sense, because the solution to the diff eq shouldn't be an exponential. Anyway, it rejected my answer too (I tried typing in 0.053)
I agree as well. I think the question should tell what the final time is, at least. There's no way there's enough information. The most I got up to was this:
The velocity of the rocket when it is switched of can be given by:
v0=1225GM(R0RR−R0)
I solved it by separating and integrating:
∫v051v0vdv=∫R0R−R2GMdR
But the question is: how do I find the final distance, when the rocket reaches constant velocity?
Edit: I managed to write the final distance as a function of time when the rocket reaches a fifth of its initial velocity. But if you aren't given the anything else, the question is impossible to solve.
Would it be right in saying that the distance from Earth as a function of time would be R=e−2GMt?
The golden question is: How is the final time related to t0?
I still don't understand. Finding the time as a function of initial time is hard, but necessary. It must be done in order to achieve a final expression!
@Karan Chatrath at t=qBmπ the velocity vector turns by 2π
I can find the displacement from origin but cannot able to find distance.
The particle has a weird trajectory, how to calculate distance travelled , Give me some clue /hint?
@Karan Chatrath the question in the book is asking for (velocity of the particle A when angle between the rods
becomes θ)
Can you show your attempt by posting a discussion ?
Thanks in advance
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
@Karan Chatrath
@Karan Chatrath will the particle come to at the rest after t=∞ ?
Log in to reply
Yes, the particle will come to rest as t→∞ since the expression for the velocity components has a decaying exponent.
@Karan Chatrath Using two initial conditions , how can we find 4 constants?
Log in to reply
vx(0)=u ; v˙x(0)=−Au ; vy(0)=0 ; v˙y(0)=Bu
You missed the above line in the note, so I am adding it here too.
Log in to reply
@Karan Chatrath oh yess sorry
If you don't mind we should not write it as B, because there are two B which leads to confusion.
Log in to reply
That is a good point. I have edited the note
@Karan Chatrath after integration of velocity , 2 more constants are waiting us.
Log in to reply
x(0)=y(0)=0
You missed this line too, so I am adding it here. Use these two conditions to solve for the constants.
@Karan Chatrath That really interesting.
I wish I could see particle whole motion in graph.
Log in to reply
I will update this note after some time. But if you put k=0⟹a=0 the particle moves in a circle as expected.
Log in to reply
@Karan Chatrath acha to fir magnetic force aur drag force barabar ho jaayega to particle ruk jayega .
Right?, aisa aisa hua to bahut interesting ho jaayega
@Karan Chatrath if you don't mind,if it takes very much time. To write all thing in latex, which maybe a waste of time, then I suggest you to use pen and page.
@Karan Chatrath After doing calculations I am getting c1=0 c2=u c3=u c4=0
Log in to reply
I have not checked this myself. But from a dimensional standpoint, the result seems okay.
I have edited the note by adding some plots. Hope this helps.
@Karan Chatrath after that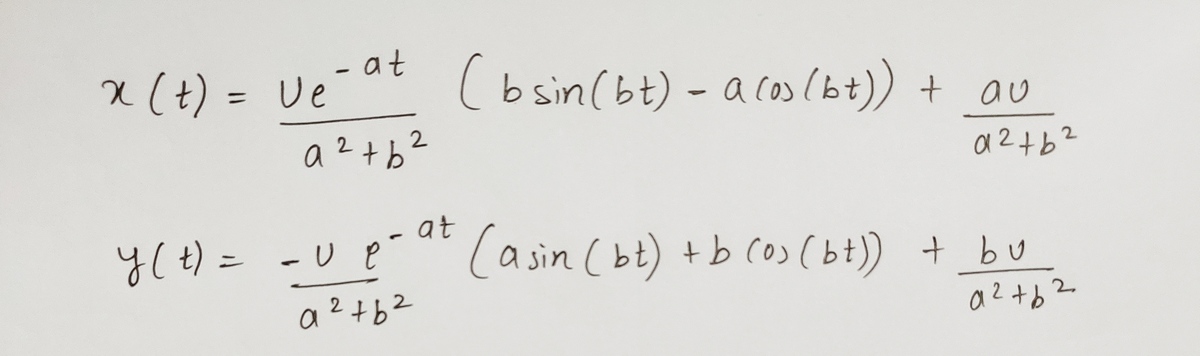
Log in to reply
Based on this, as t→∞:
xD=a2+b2au yD=a2+b2bu
@Karan Chatrath and yes the answer is D=q2B2+k2kmui+q2B2+k2qBmuj
Greetings we just rocked!
But your contribution is 95% :)
Log in to reply
Well done! Glad that I could help
Log in to reply
@Karan Chatrath You help always. Love you sir .
But this was very difficult, what do you think.
Log in to reply
Solving by hand makes this a difficult problem. It is easy to make calculation mistakes
@Karan Chatrath
I was looking at phase portraits earlier; thanks for this one!
Log in to reply
The plots that I have shared are not phase portraits.
Log in to reply
Yeah; I know that; these are trajectories, but they look like phase portraits of pendulums with drag.
@Karan Chatrath Yeah it worked finally.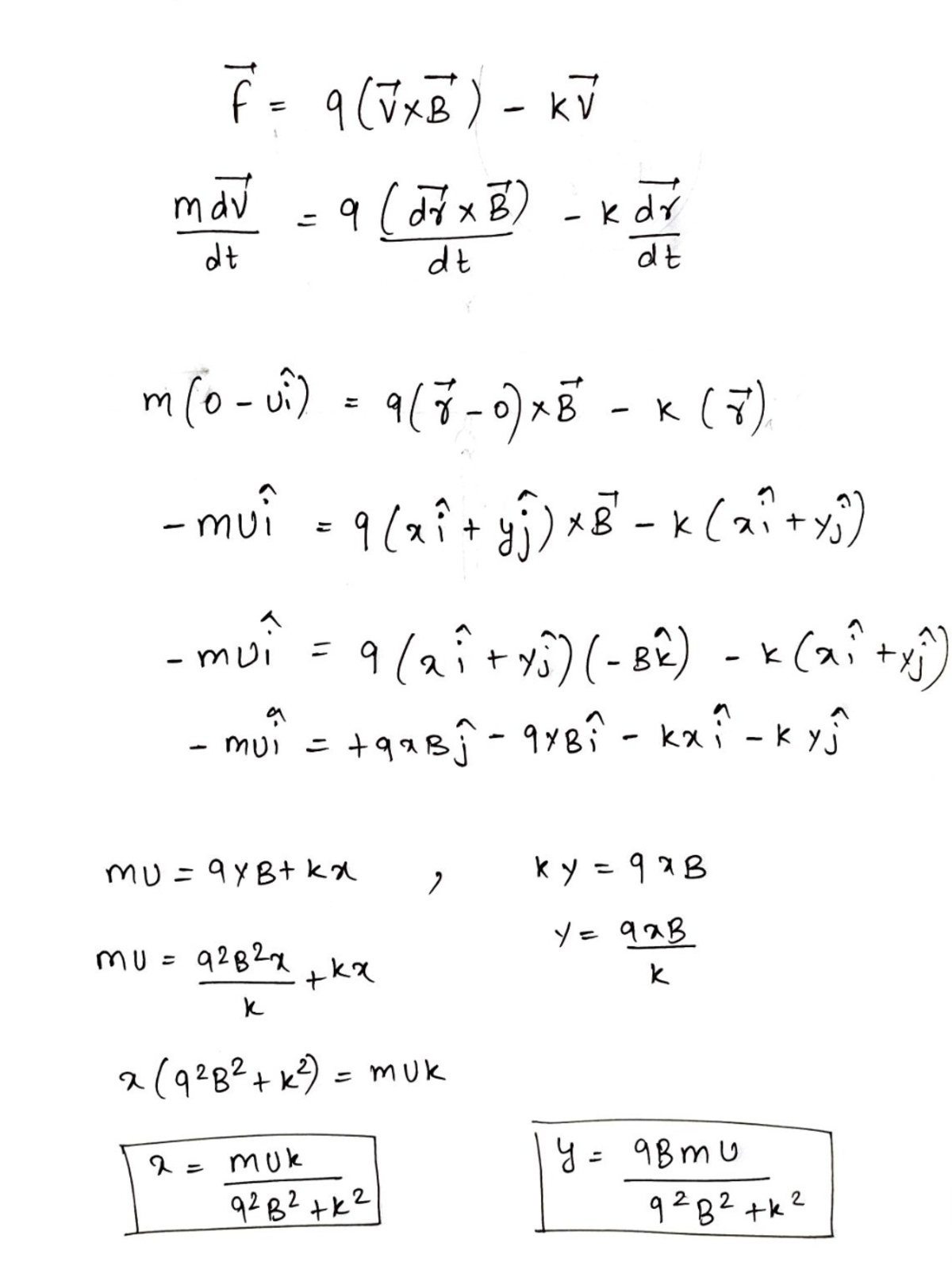
The difference between your and my method is that , by your method we can find location of particle at any time t, and in my method I have just focused on where the particle stops.
Reply if you found it good.
Log in to reply
Yes, this is a faster way of solving the problem. Well done.
@Lil Doug By the way, this is the same problem as the damping one you wanted me to solve, just with a little different final quantity to be solved for. Latex is being very buggy in the notes section, and I just lost a bunch of work trying to post the solution.
Log in to reply
@Steven Chase No problem :)
@Steven Chase I am not able to understand only that last line (velocity vector turns my 2π
Can you help me to understand that line.
Thanks in advance.
Hope I am not disturbing you.
Log in to reply
The motion is described in terms of sinusoids of a certain frequency. You can find out what the time period is for the sinusoids, and evaluate the motion up until one time period has elapsed.
Log in to reply
@Steven Chase sir i think the problem is whole same, except last line.
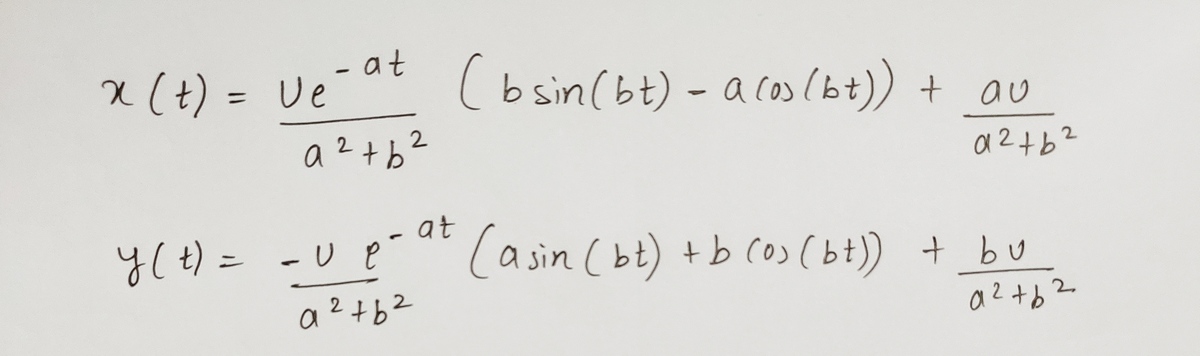
I have provided x(t) and y(t)
Can you do something from this data? Thanks in advance. Hope I am not disturbing you
@Karan Chatrath Try this problem.
@Karan Chatrath
Log in to reply
I will try it, but I want to see your attempt before I post mine. Also, I posted a report on your problem titled 'Spaceship Mechanics'. Could you please get back to me on that?
Log in to reply
@Karan Chatrath Yes sir, sorry I didn't reply you for that report.
The question is basically copied through the book, I checked it many times, there is nothing more than that given in question.
Can you please try to think it by seeing the graph.
Log in to reply
t0 I think is the time when the engine is turned off
@Karan Chatrath
About your report, t0 is when the engine is turned off, I think.
Is the answer the following?
D=bmvo(1−e−qB2πb)
Log in to reply
@Karan Chatrath yes it's CORRECT
Log in to reply
@Lil Doug Lol that's a funny way of saying correct. lmao. You gave me a fright.🤣
Log in to reply
@Krishna Karthik he is my favorite teacher.
He is just awesome bro.
Therefore I done that. His skills of solving problem are better than even Einstein sir.
Log in to reply
What set Einstein apart was creativity, not problem-solving. But, both do go hand in hand in some way. He is quite remarkable, Karan Chatrath.
@Krishna Karthik @Karan Chatrath I have made changes in the spaceship mechanics problem, the time at which the rocket turned off is t0
Log in to reply
Please tell me. How do I do the rocket problem?
Log in to reply
@Krishna Karthik I have also posted for solution 😜
I was also not able to solve that.
Log in to reply
Here's what I got up to:
The velocity of the rocket when it is switched of can be given by:
v0=1225GM(R0RR−R0)
I solved it by separating and integrating:
∫v051v0vdv=∫R0R−R2GMdR
But the question is: how do I find the final distance, when the rocket reaches constant velocity?
Hi Krishna, please refrain from using swear words on Brilliant. I've updated your comment.
@Krishna Karthik it seems me that you are very interested in rocket.
Log in to reply
It's an interesting question.
@Krishna Karthik Hope @Karan Chatrath will post a solution of Spaceship Mechanics
Log in to reply
@Lil Doug I really do. That one baffles the shit out of me. Btw did you see my approach on it?
The velocity of the rocket when it is switched of can be given by:
v0=1225GM(R0RR−R0)
I solved it by separating and integrating:
∫v051v0vdv=∫R0R−R2GMdR
But the question is: how do I find the final distance, when the rocket reaches constant velocity?
Log in to reply
@Krishna Karthik Bro let me try again the problem.
Log in to reply
Is my approach correct? Btw did you also start with this? Also, you can do this by linking using the work energy theorem (no differential equation solving there):
Ui=R−GMm
Uf=R0−GMm
501mv02−21mv02=Uf−Ui
You can get the exact same result with the above method.
Log in to reply
@Krishna Karthik I don't know because I didn't have tried the problem with even 50% of my full potential
I was feeling lazy, just posted it bro.
Log in to reply
No worries my dude. This kind of problem; yikes. People in SpaceX working for Elon Musk be trynna solve this shit...
Log in to reply
@Krishna Karthik is Elon Musk sir is in Brilliant.?
Log in to reply
Lol nope. Yeah; people there would struggle solving this problem. SpaceX is extremely good with their rockets.
Log in to reply
@Krishna Karthik what is the meaning of “people there would struggle solving this problem.“
I don't think people of spacex will difficulty to solve that problem.
Log in to reply
Not really, but it's still super hard to do by pencil and paper. Besides, real rocket engineers probably haven't tried a problem under exam conditions in ages.
But this is a really tough one with lots of mathematically hard stuff. If you can somehow find Stephen Hawking in heaven and bring him back to Earth, he'll do it for you :)
Log in to reply
@Krishna Karthik I agree.
Now I have some work, I am going, we will talk tomorrow regarding rocket problem .
By the way within 20min a new song of my favorite singer is coming, so I am very excited.
Bye.
Log in to reply
Ok bud. See ya. I've gotta go to sleep anyway.
@Krishna Karthik where did karan sir gone.
He was talking with us
Log in to reply
Let him be in peace. He should focus in order to solve the problem.
@Karan Chatrath i have made necessary changes in the spaceship Mechanics.
Please delete the report.,
And within some hours I will post a note showing my attempt on that charge problem.
Log in to reply
I have tried that problem and I do not know how to solve it. In my opinion, the available information is inadequate, but I may be wrong.
Log in to reply
I thought the problem was telling us that 5t0 was the time it took for the velocity to drop to e−5v0. Like a "five time constant" thing. Which doesn't quite make sense, because the solution to the diff eq shouldn't be an exponential. Anyway, it rejected my answer too (I tried typing in 0.053)
I agree as well. I think the question should tell what the final time is, at least. There's no way there's enough information. The most I got up to was this:
The velocity of the rocket when it is switched of can be given by:
v0=1225GM(R0RR−R0)
I solved it by separating and integrating:
∫v051v0vdv=∫R0R−R2GMdR
But the question is: how do I find the final distance, when the rocket reaches constant velocity?
Edit: I managed to write the final distance as a function of time when the rocket reaches a fifth of its initial velocity. But if you aren't given the anything else, the question is impossible to solve.
Would it be right in saying that the distance from Earth as a function of time would be R=e−2GMt?
The golden question is: How is the final time related to t0?
@Steven Chase @Karan Chatrath
@Steven Chase @Karan Chatrath I have posted the problem again with right answer here
@Karan Chatrath Does your answer of spaceship Mechanics problem matches with @Steven Chase sir's answer.
His answer is around 0.053 ?
@Steven Chase @Karan Chatrath @Krishna Karthik i have changed the graph little bit and added Note on the problem spaceship Mechanics.
I hope the problem is clearly stated now.
Log in to reply
I still don't understand. Finding the time as a function of initial time is hard, but necessary. It must be done in order to achieve a final expression!
@Karan Chatrath sir if you don't mind, there is an error in 15th line of solution it should be a2+b2
Log in to reply
Good catch. It is corrected now.
@Karan Chatrath at t=qBmπ the velocity vector turns by 2π
I can find the displacement from origin but cannot able to find distance. The particle has a weird trajectory, how to calculate distance travelled , Give me some clue /hint?
Log in to reply
No, the time you have computed is incorrect.
For distance:
ds=V dt Where V is the speed.
Log in to reply
@Karan Chatrath after 20 minutes I am going to post a note sharing my attempt Please be active after 20 minutes.
@Karan Chatrath the attempt is posted.
@Karan Chatrath
Sir i want to see your solution. Share whenever you will be free.
Thanks in advance.
@Karan Chatrath the question in the book is asking for (velocity of the particle A when angle between the rods becomes θ)
Can you show your attempt by posting a discussion ?
Thanks in advance
Log in to reply
Which question? I would use Lagrangian mechanics.
Log in to reply
Mechanics |17-09-2020|
Log in to reply
I'm trying it out right now. I'm trying to create a time-domain simulation.
I will create a note after some time.