Triangle Centers

Circumcenter:

The perpendicular bisectors of a triangle are concurrent . And the point of their concurrence is known as "Circumcenter". Basically, it is represented by '$S$'.

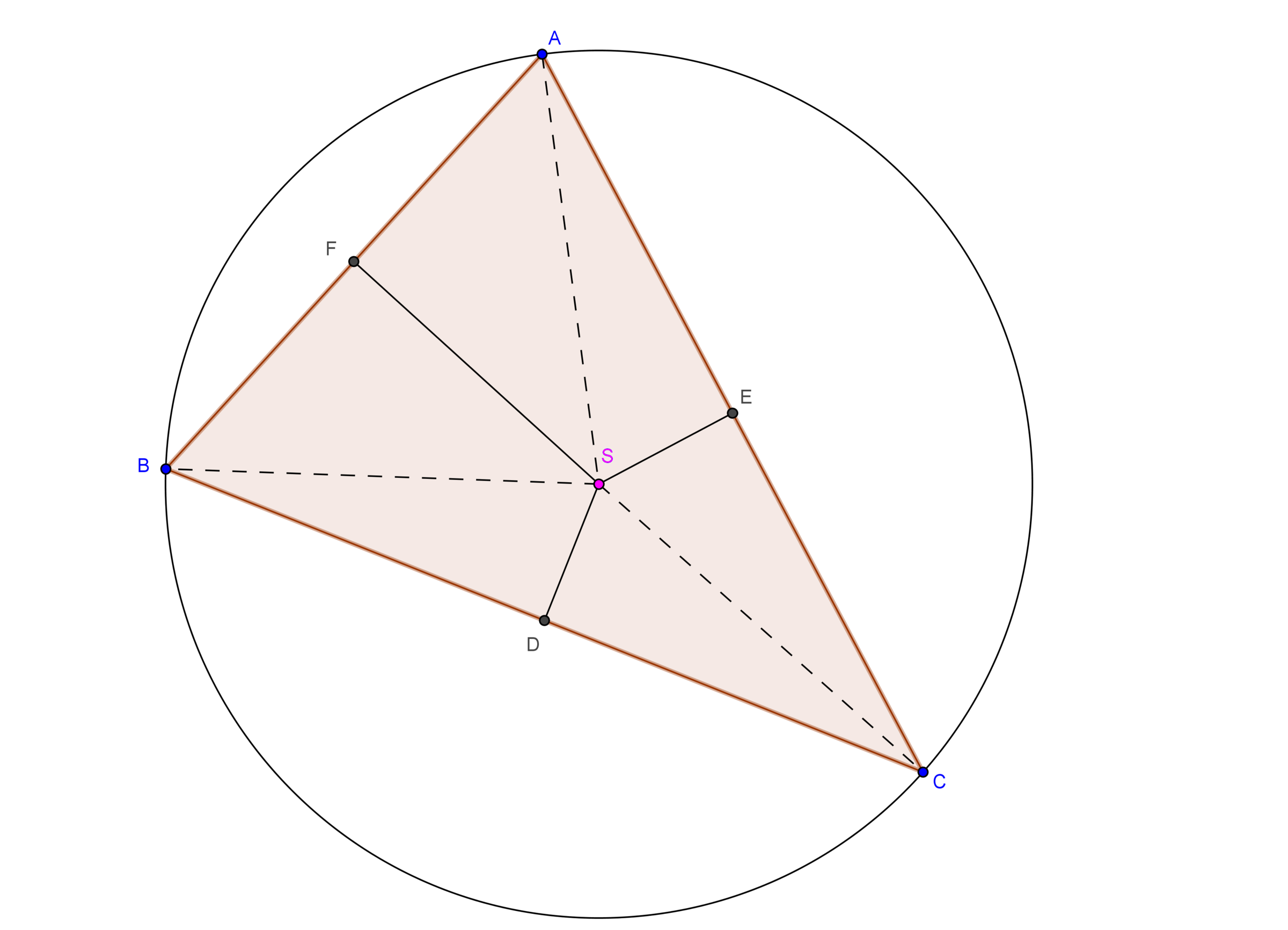
The circumcenter is equidistant from all the three vertices. So, how can we say that the perpendicular bisectors are concurrent and circumcenter is equidistant from all the three vertices. So, we shall prove that. But how??? So, first draw the perpendicular bisectors of sides $BC$ and $AC$. Let they intersect at $S$. Now, drop a perpendicular from $S$ onto $AB$. Let this perpendicular meet $AB$ at $F$. So, it is sufficient to prove that $SF$ is the perpendicular bisector of $AB$.

So, observe that $BD=DC$ (why?) and $\angle BDS = \angle CDS = 90^{o}$. So, $\Delta BDS \cong \Delta CDS$. So, $SB = SC$. Similarly proceeding for $\Delta AES$ and $\Delta CES$, we obtain $SC =SA$. This implies that $SA = SC$. So, $\Delta SAC$ is isosceles. Then what can we say about the altitude $SF$ of $\Delta SAB$. It is also the perpendicular bisector of the side $AB$.(But why?). So, we have finally proved.$\blacksquare$

So, let's move onto next topic.

Incenter:

The internal angular bisectors of the angles of the triangle are concurrent. The point of concurrence of these angular bisectors is known as "Incenter". It is represented by the letter '$I$'. And the radius of the incircle is the perpndicular distance from Incenter to any one the side.

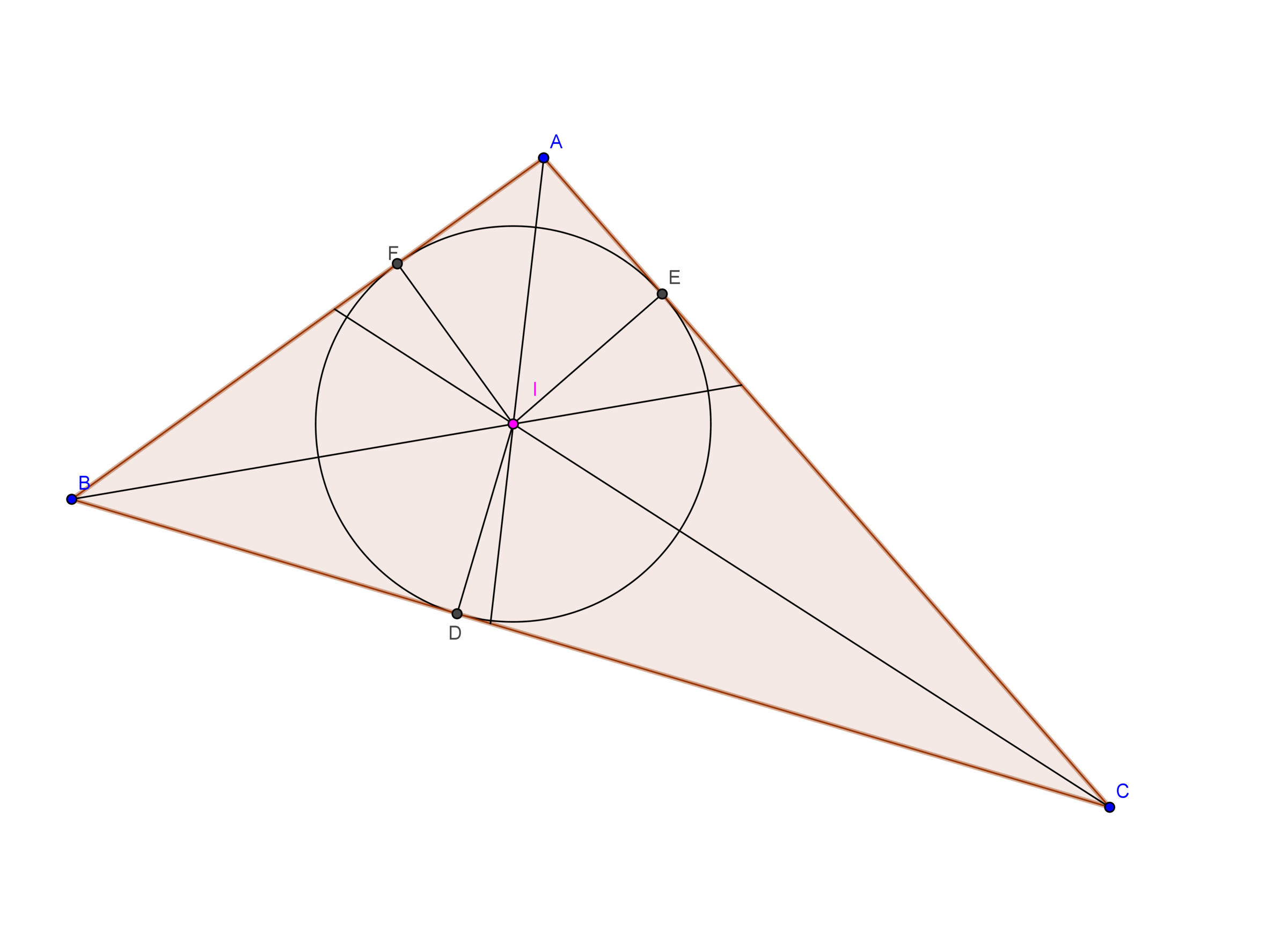
So what is the special property of this Incenter. Actually, it is equidistant from all the sides of the triangle. So, How can we prove these things as like above? Can we use the similar strategy to that? Of Course, we can prove this using the above strategy.

So,let us first draw the angular bisectors of $\angle A$ and $\angle B$. Let they meet at $I$. So, if we prove that $CI$ is the angular bisector of $\angle C$, we are done. But how? Let $ID$,$IE$ and $IF$ be the perpendiculars from $I$ onto the sides $BC$, $CA$ and $AB$.

Observe that, $\angle DBI = \angle FBI$ and $\angle IDB = \angle IFB = 90^{o}$. So, $\Delta IBF \cong \Delta IBD$. So, $ID =IF$. Applying similar procedure for $\Delta IFA$ and $\Delta IEA$, we get $IE = IF$. This implies that $ID = IE$. But, $\angle IDC = \angle IEC = 90^{o}$. So, $\Delta IDC \cong \Delta IEC$. But what can we infer from this?? Oops, actually we're done.(How? Think yourselves). So, we have finally proved this. Are you feeling bored? I think you won't. So, Let's move on. $\blacksquare$

Orthocenter:

So, what is this orthocenter? Can you guess it? Okay, right. Actually, Orthocenter is the point of concurrence of the altitudes of triangle. It is generally represented by the letter '$H$.

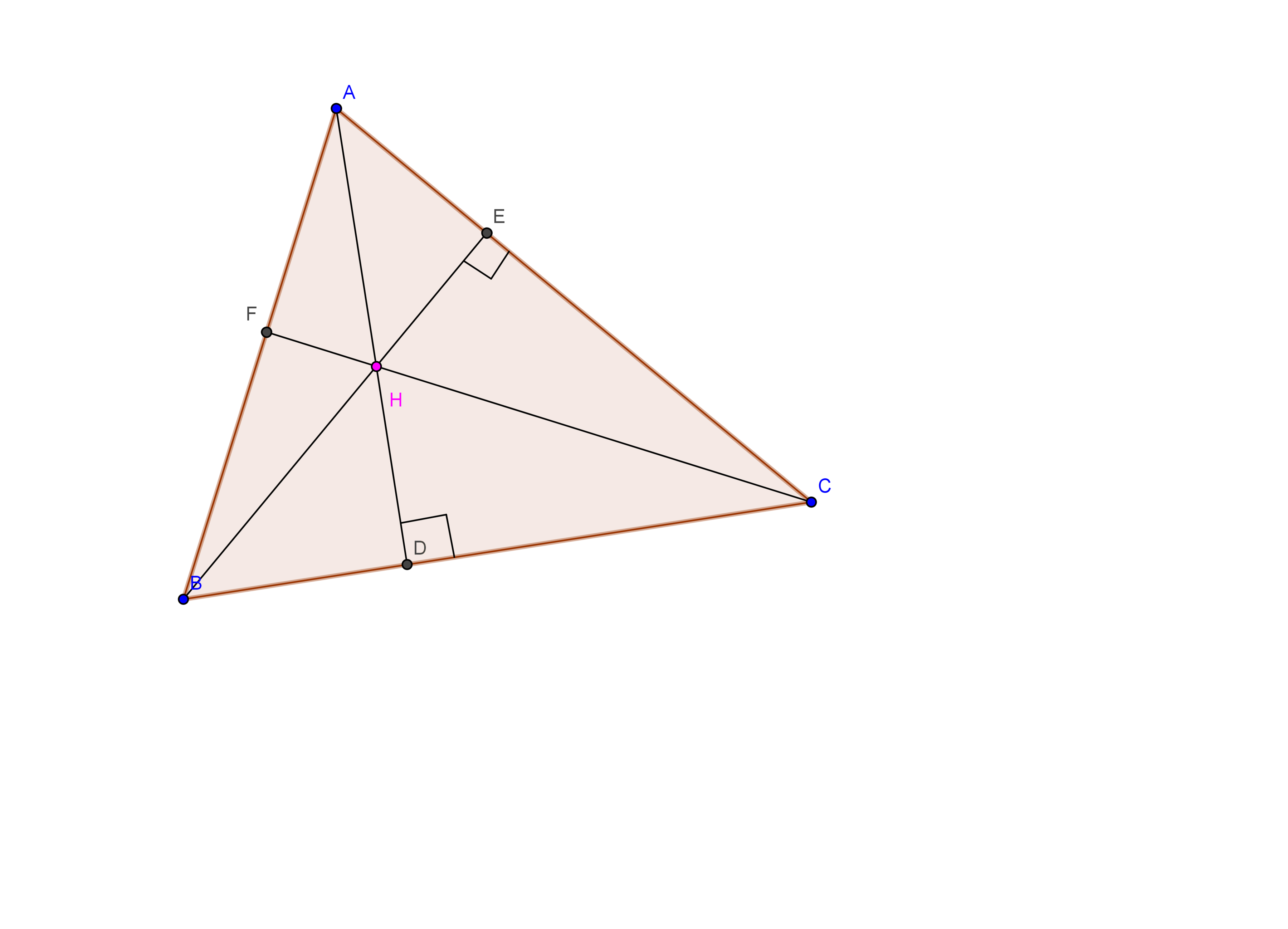
So, how to prove this? Apply the same strategy as before. In $\Delta ABC$, let $AD$ and $BE$ be the altitudes through $A$ and $B$ onto $BC$ and $CA$ respectively. Let they meet at the point '$H$'. Extend $CH$ to meet $AB$ at $F$. So, we have to prove that $CF$ is perpendicular to $AB$.

Since, $\angle AEB = \angle ADB = 90^{o}$, it infers that $AEDB$ is cyclic quadrilateral. Also, $\angle HEC + \angle HDC = 90^{o} + 90^{o} = 180^{o}$. So, $HECD$ is cyclic quadrilateral. Now, $\angle BAD = \angle BED = 90^{o} - \angle CED = 90^{o} - \angle CHD$. But, $\angle BAD = 90^{o} - \angle ABC$. So, $\angle ABC = 90^{o} - \angle BAD = 90^{o} - (90^{o} - \angle CHD) = \angle CHD$. Now, $\angle FHD = 180^{o} - \angle CHD = 180^{o} - \angle BAC$. So, $BFHD$ is cyclic. This implies that $\angle BFH = 180^{o} - \angle BDH = 90^{o}$. Phewww!! We're done. Finally proved it. Did you observe that the orthocenter of $\Delta ABC$ is the incenter of $\Delta DEF$.(But How? Try it yourselves)

Before moving to Centroid, let us first discuss about Ceva's Theorem.

Ceva's Theorem:

Consider three concurrent line $AD$,$BE$ and $CF$ which are concurrent at $P$. Then, $\dfrac{BD}{DC} . \dfrac{CE}{EA} . \dfrac{AF}{FB} = 1$

Let us prove this. Draw a line parallel to $BC$ through $A$. Extend $BE$ and $CF$ to meet this parallel line at $B'$ and $C'$. We can observe that there are so many similar triangles formed here.

As $\Delta AFC' \sim \Delta BFC$ and $\Delta AEB' \sim \Delta BEC$, we have $\dfrac{AF}{FB} = \dfrac{AC'}{BC}$ and $\dfrac{CE}{EA} = \dfrac{BC}{AB'}$.

As $\Delta APC' \sim \Delta CPD$ and $\Delta APB' \sim \Delta BPD$. So, $\dfrac{AB'}{BD} = \dfrac{PA}{PD}$ and $\dfrac{AC'}{CD} = \dfrac{PA}{PD}$.

This implies that $\dfrac{AB'}{BD} = \dfrac{AC'}{CD}$. So, $\dfrac{BD}{CD} = \dfrac{AB'}{AC'}$.

$\dfrac{BD}{DC} . \dfrac{CE}{EA} . \dfrac{AF}{FB} = \dfrac{AB'}{AC'} . \dfrac{BC}{AB'} . \dfrac{AC'}{BC} = 1$. Hence, proved.

Let us move onto centroid.

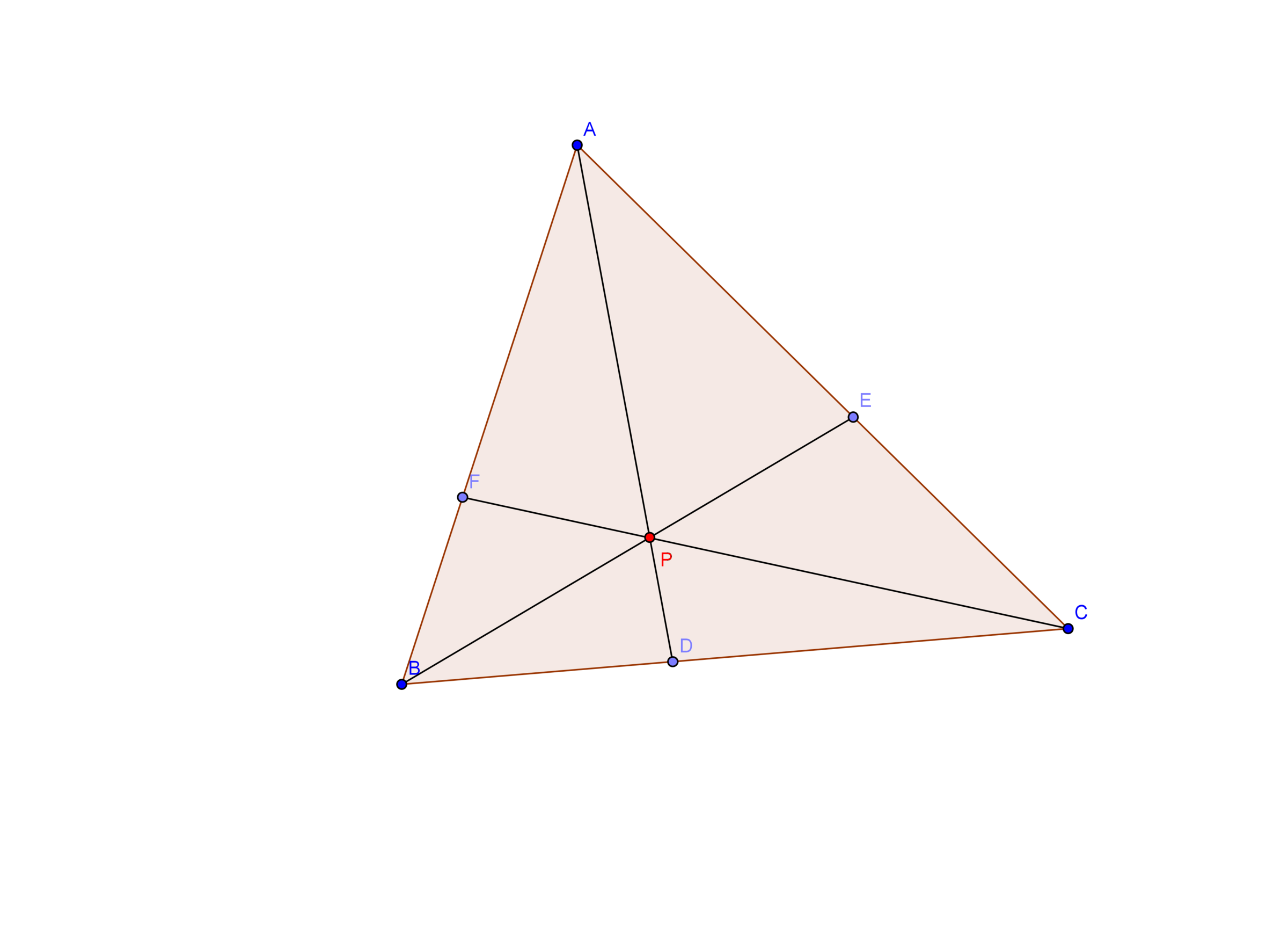
Centroid:

Centroid is the point of concurrence of medians of a triangle. It is generally denoted by '$G$'.

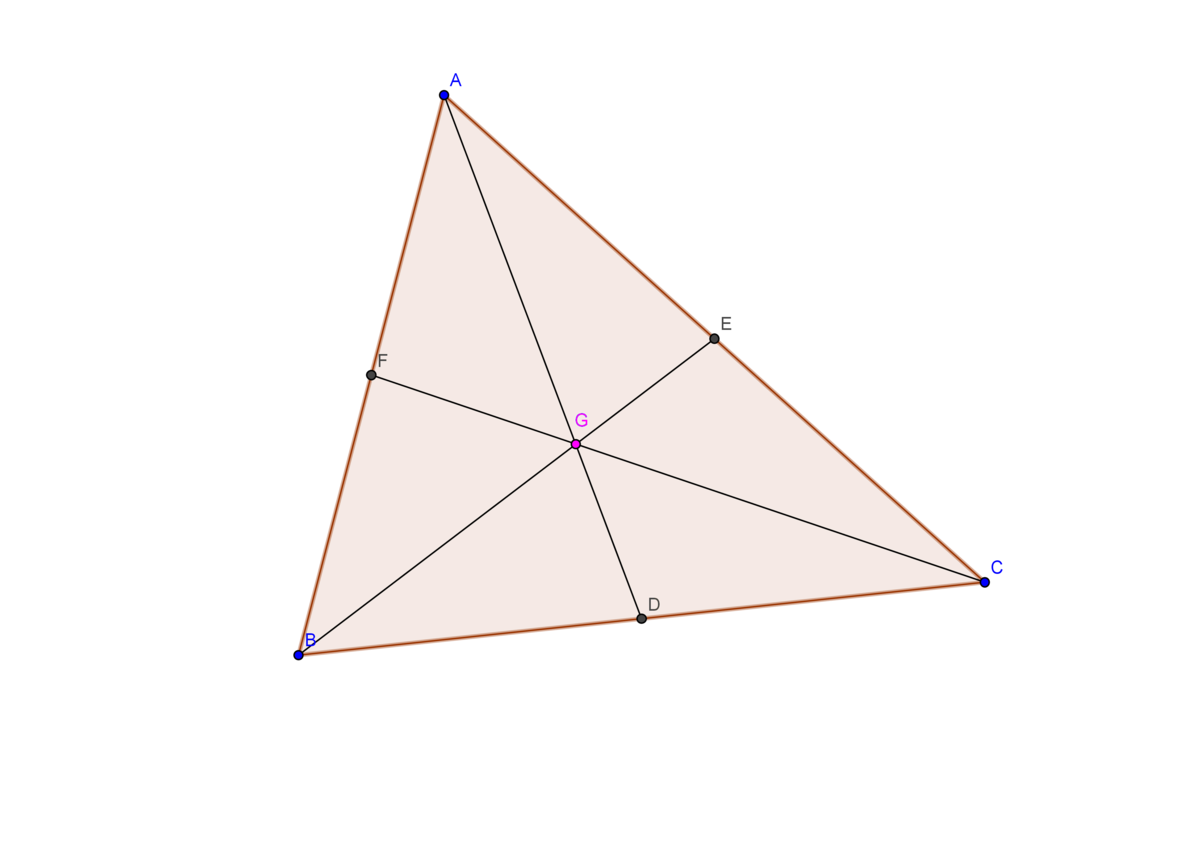
So, it is very easy to prove this. Let $AD$ and $BE$ be the medians. We have to prove that $CF$ is also a median.

From Ceva's Theorem,

$\dfrac{BD}{DC} . \dfrac{CE}{EA} . \dfrac{AF}{FB} = 1$

But $D$ and $E$ are the midpoints of $BC$ and $CA$. So, $BD = DC$ and $CE = EA$.

So, $\dfrac{AF}{FB} = 1$. It implies that $AF= FB$. So, $F$ is the midpoint of $AB$ which infers that $CF$ is the median. So, the three medians of a triangle are concurrent.

$\blacksquare$

Excenter:

Excenter is the point of concurrence of external angular bisector of two vertices and internal angular bisector of the third vertex.

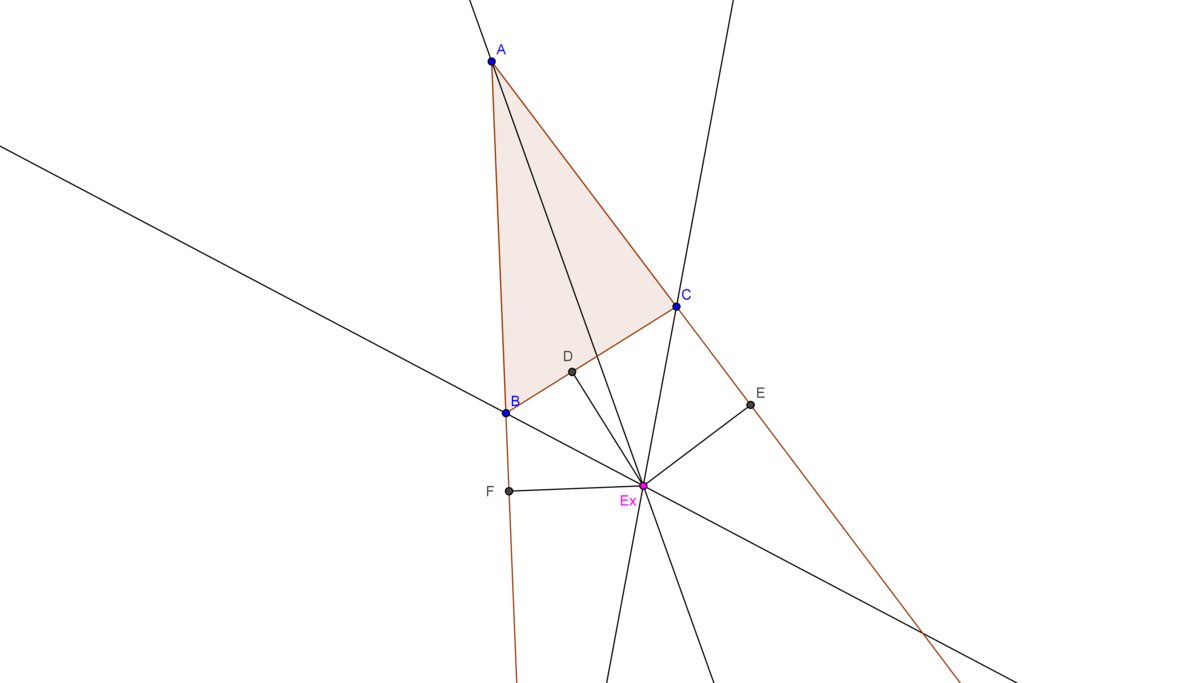
So, Let us prove that these lines are concurrent.

Draw the external angular bisectors of $\angle B$ and $\angle C$. Let they meet at $E_{x}$. We have to prove that $AE_{x}$ is the excenter of $\angle A$. Draw the perpendiculars $E_{x}D$, $E_{x}$ and $E_{x}F$ from $E_{x}$ onto $BC$,$CA$ and $AB$ respectively.

As, $\angle FBE_{x} = \angle DBE_{x}$ and $\angle BFE_{x} = \angle BDE_{x}$, it infers that $\Delta BDE_{x} \cong \Delta BFE_{x}$. So, $E_{x}D = E_{x}F$. Similarly $E_{x}F=E_{x}E$. So, $E_{x}D = E_{x}E$. But $\angle AFE_{x} = \angle AEE_{x} = 90^{o}$. It implies that $\Delta AFE_{x} \cong \Delta AEE_{x}$. So, $\angle BAEx = \angle CAE_{x}$. It implies that $AE_{x}$ is the internal angular bisector of $\angle A$. Hence, proved. $\blacksquare$

Till now we had studied about Circumcenter, Incenter, Orthocenter, Centroid and Excenter. Let us move onto some what advanced.

Nine Point Circle:

The nine point circle is named so because it passes through the nine points of the circles . These nine points are:

1. Midpoint of each side.

2. The of each altitude.

3. The midpoint of line segment from each vertex of the triangle to the orthocenter.

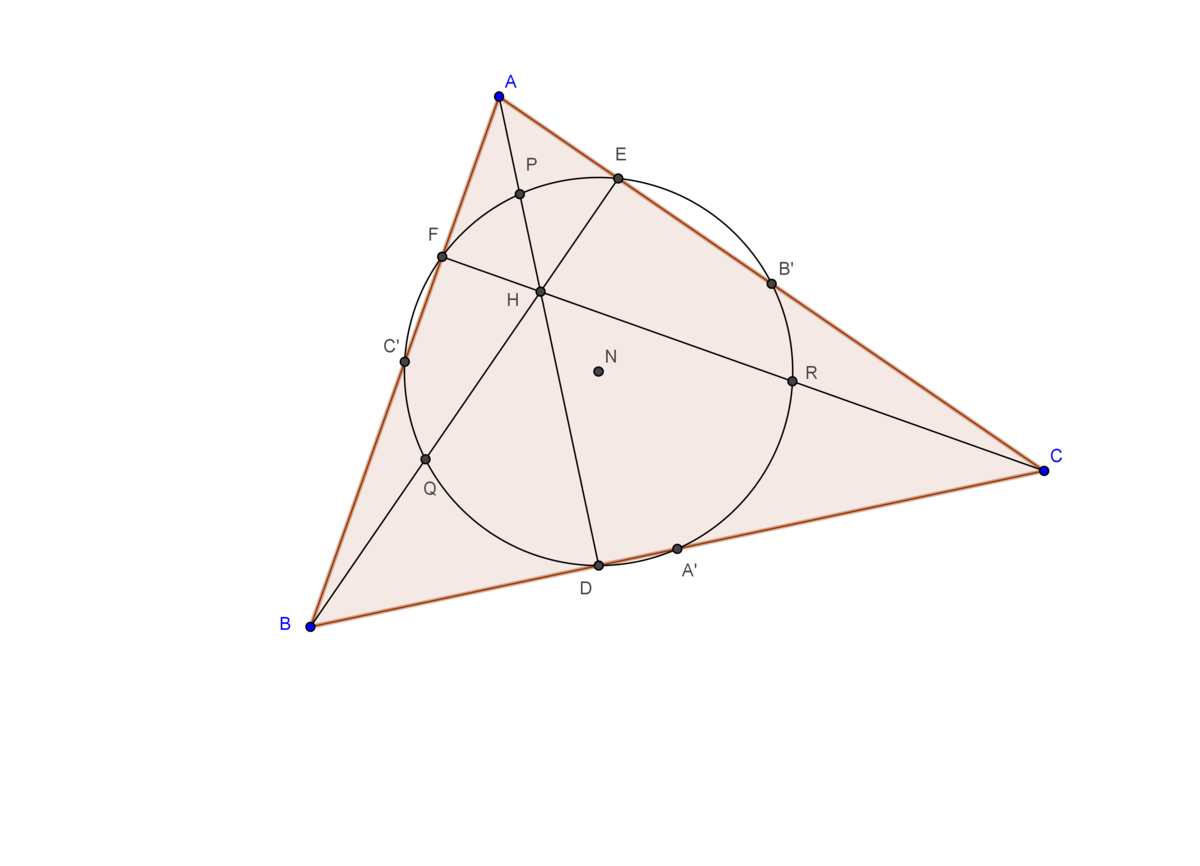
This means that these nine points are concyclic. But how can we say that they are concyclic? Let us prove it.

Consider $\Delta ABC$. Let $AD$, $BE$ and $CF$ be the altitudes from $A$, $B$ and $C$ respectively. Let $A',B',C',P,Q,R$ be the mid points $BC,CA,AB,AH,BH,CH$ respectively.

From, $\Delta ACH$, we get $B'R = \frac{1}{2}AH$ and $B'R||AH$.

From $\Delta ABH$, we get $C'Q = \frac{1}{2}AH$ and $C'Q||AH$.

So, $B'R = C'Q$ and $B'R||C'Q$.

But, $B'C' ||BC$, $QR||BC$ and $AH \perp BC$.

So, $B'C' || QR$ and $C'Q||AH \perp B'C'$. It implies that $B'C'QR$ is rectangle and so it is cyclic. Similarly, $A'B'PQ$ and $A'C'PR$ are cyclic. This forces that $A', B', C', P, Q, R$ are cyclic.

As $\angle B'EQ = 90^{o}$ and $\angle B'CQ = 90^{o}$(Since we proved before.) It implies that $\angle B'EQ = \angle B'CQ$. It forces that $E$ is also concyclic with these points. Similarly, $D,F$ are also concyclic with these points. So, $A,B,C,A',B',C',P,Q,R$ are concyclic. Hoofff!!! Done. $\blacksquare$

Till now we have discussed about Circumcenter, Incenter, Orthocenter, Centroid, Excenter, Nine point center. Now, let us discuss about

1. Radius of Nine Point Circle.

2. Relation between Circumcenter, Nine Point Center, Orthocenter and Centroid.

Radius of Nine Point Circle:

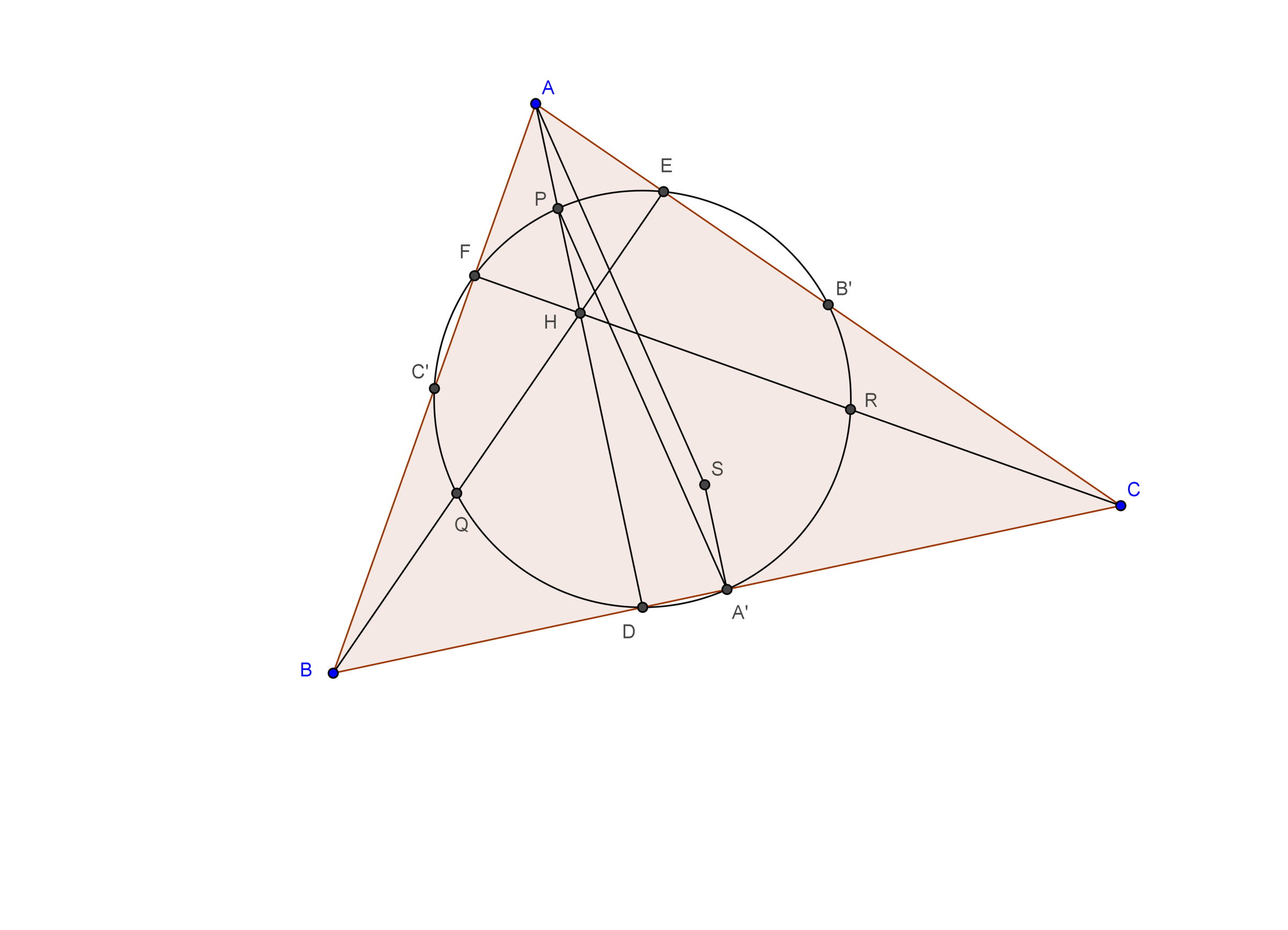
From the fact that radius of circumcircle of rectangle is half the diameter of the rectangle. It is sufficient to find the length of $A'P$. Because $A'P$ is the diagonal of the rectangle $A'B'PQ$ which are on the nine point circle.

Let $BC = a$, $AC=b$ and $AB =c$. And let $A,B,C$ represent $\angle BAC, \angle ABC , \angle ACB$. Observe that $CDHE$ is cyclic. So, $\angle AHE = 180^{o} - \angle DHE = C$.

$AH = \dfrac{AE}{Sin \angle AHE} = \dfrac{AB Cos \angle BAE}{Sin C} = \dfrac{c}{Sin C} Cos A = 2RCos A$

But, since angle subtended by the arc at the center is double the angle subtended by the arc at any point on the circle, $\angle BSC = 2A$. As $\angle BSA' = \angle CSA'$. It implies that $\angle CSA' = A$. So, $SA' = SA CosA = R CosA = \frac{1}{2}AH = AP$.(where 'R' is the circumradius.)

Now, $AD \perp BC$ and $SA' \perp BC$, it forces that $AD||SA'$. And, as we proved before that $AP = SA'$, it infers that $APA'S$ is a parallelogram. So, $AP = SA = R$. So the radius of the nine point circle is equal to half the length of $AP$ which is equal to $\frac{1}{2} R$. Finally, achieved it. $\blacksquare$

Relation between 'H', 'N','G' and 'S' :

First let us prove that centroid divides the median in the ratio of $2:1$.

Consider $\Delta ABC$. Let $AD, BE, CF$ be the medians and let $G$ be the centroid. Reflect $A,G, E$w.r.t the line $BC$ and let them be $A',G',H$. As $BF = CH$ and $BF||CH$. It implies that $BFCH$ is parallelogram. So, $FC||BH$. But since $AF = FB$. It infers that $AG = GG'$. But $GG' = \frac{1}{2}GD$. So, $AG = \frac{1}{2}GD$ and it infers our result that $AG:GD = 2:1$.

So, how far does this result help us?

Before starting this, Did you observe that nine point center is actually the circumcenter of the triangle formed by joining the midpoints of the sides of the triangle?(But how? Think yourselves.). Let us move on.

Actually, in any triangle the circumcenter, orthocenter, centroid and nine point center lie on the same line. And this line joining them is known as Euler's line.

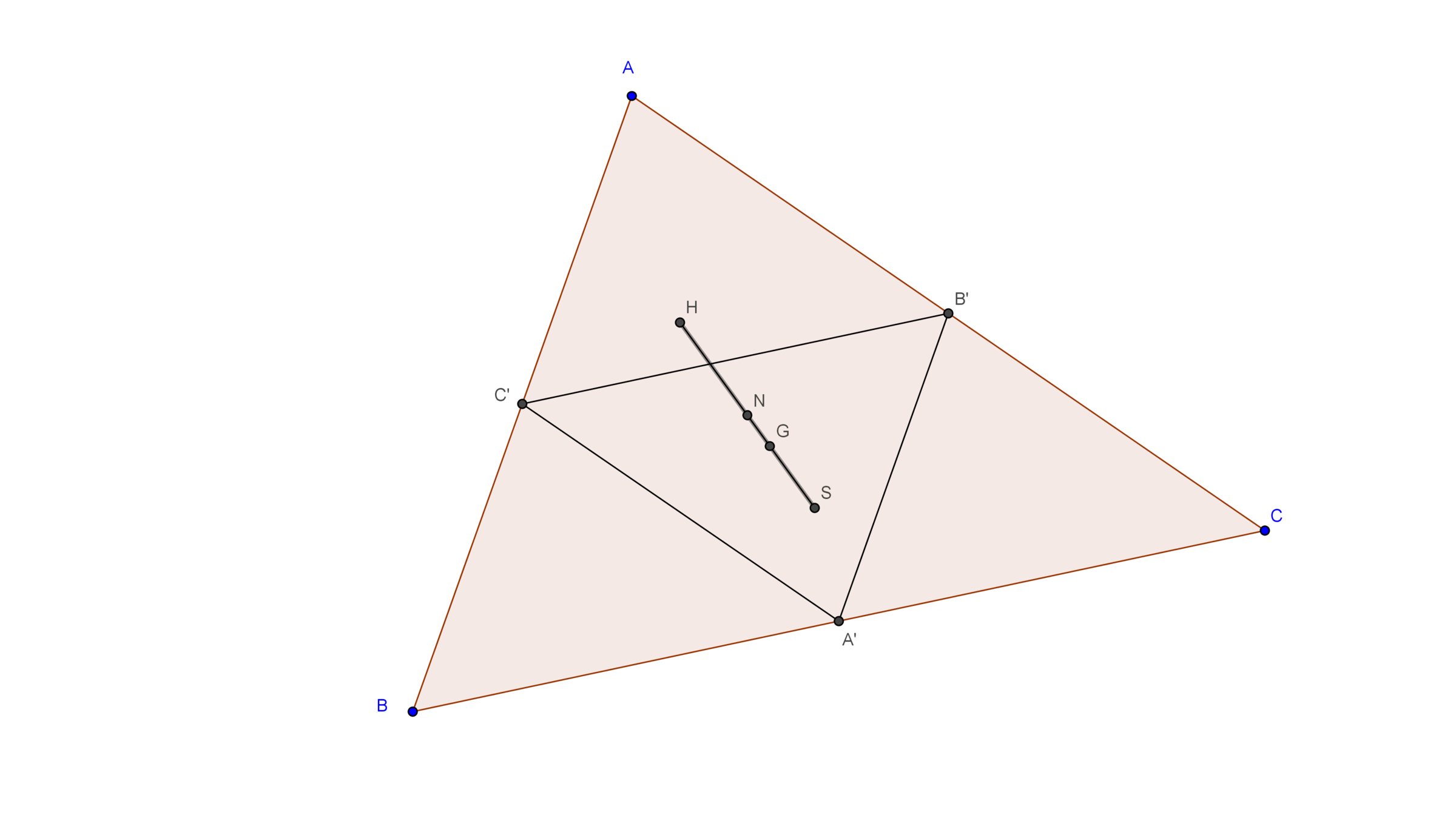
So, the proof for this very interesting. First, observe that $BC||B'C'$ and $A'S \perp BC$ and it implies that $B'C' \perp A'S$. Similarly $A'B' \perp C'S$. It implies that $S$ is the orthocenter of $\Delta A'B'C'$ which is the circumcenter of $\Delta ABC$.

Now, since $AG = 2GD$. Let us do operation. By squeezing $AG$ to half and reflecting it w.r.t $G$, we get $A'$. Similarly, doing this operation to $B$ and $C$, we get $B'$ and $C'$. So, circumcenter of $\Delta ABC$ transforms to circumcenter of $\Delta A'B'C'$, i.e. $S$ transforms to $N$. So, $\frac{1}{2}SG = NG$. We have proved that $S$, $G$ and $N$ are collinear.

Next, Do the same operations. So, Orthocenter of $\Delta ABC$ transforms to orthocenter of $\Delta A'B'C'$,i.e. $H$ transforms to $S$. It infers that $\frac{1}{2}HG = SG$. $\blacksquare$

So, from the above two facts, it implies that $HN:NG:GS = 3:1:2$. Pheww!! Finally the note is completed.

In this note I had proved all the proofs only considering that the triangle is acute angled. So, it's your turn to try them to prove for obtuse angled triangle.

So, that's all for now. I will post some more advanced topics in a few days or more.