Trigonometric Identities

When students are first exposed to trigonometric identities, they are often given a list of formulas, which they are asked to memorize. Here is a way for you to remember many of these ideas.

Start by drawing a regular hexagon and connect each of the vertices to the center. Label the left-most vertex $\tan$, label the bottom left vertex $\sin$, and label the bottom right vertex $\cos$. Label the center 1. Now, to figure out how to label the remaining vertices, simply look at the diagonally opposite vertex and label it as the reciprocal. You should get the following diagram:

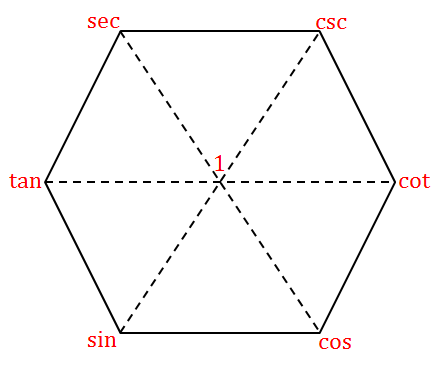Hexagon of Trigonometric Functions

(Note: $\frac {1}{ \cos \theta} = \csc \theta$, which is sometimes denoted as cosec $\theta$. Either version is valid, and we will be using $\csc$ in this post.)

Now, let's figure out some properties of this hexagon.

Property 1: How do the labels on the endpoints of a diameter relate? Recall that to establish the labels, we labelled the diagonally opposite vertex as the reciprocal. Hence, the product of the labels on a diameter is 1, which corresponds to the center vertex.

Property 2: How do we relate vertices that are connected by edges? Consider the central vertex 1. Moving directly to the left is equivalent to multiplying by $\tan$, moving to the lower right is equivalent to multiplying by $\cos$, moving to the lower left is equivalent to multiplying by $\sin$. This seems obvious when we're at vertex 1, and in fact holds true for any other vertex. For example, moving left from $\cos$ brings us to $\sin$, which corresponds to $\cos \theta \times \tan \theta = \sin \theta$. There are similar statements for moving to the right, upper left and upper right.

Property 3: What property do we get when reading off the 3 vertices in an anti-clockwise manner? With our 3 starting vertices, we know that $\tan \theta = \frac {\sin \theta} { \cos \theta}$. This behavior holds true for the rest, that the first vertex is equal to the second divided by the third. For example, another set of 3 vertices is $\cos, \cot, \csc$, and you should be able to verify that $\cos \theta = \frac { \cot \theta} { \csc \theta}$.

Property 4: Recall the Pythagorean identity which states that $\sin^2 \theta + \cos ^2 \theta = 1^2$. How is this expressed in the hexagon? If we look at the bottom upright triangle, we see it it has vertices of $\sin, \cos$ at the base, and $1$ at the top. In fact, given any other upright triangle, a similar relation holds. For example, with the right upright triangle, we get $1^2 + \cot ^2 \theta = \csc ^2 \theta$, and with the left upright triangle, we get $\tan^2 \theta + 1 = \sec^2 \theta$.

Worked Examples

1. What is $\frac {\sec \theta} { \tan \theta}$?

Solution: By property 3, we know that $\csc \theta = \frac { \sec \theta} { \tan \theta}$.

2. Why does property 4 hold?

Solution: We already know that $\sin ^2 \theta + \cos^2 \theta = 1^2$. Consider what happens when we shift this triangle to the upper right. We are simply multiplying each vertex by $\sec \theta$. Hence, the equivalent identity is that $\sec^2 \theta [ \sin ^2 \theta + \cos^2 \theta] = \sec^2 \theta \cdot 1^2$, which becomes $\tan^2 \theta + 1^2 = \sec^2 \theta$.

3. What other properties are there?

Solution: This is an open ended question. There are as many properties as you can find for yourself. We will state one more, which is related to Property 3 (and actually is simply a different way of expressing the same idea):

Property 5: If we read a set of 3 vertices off in a clockwise-order, we get that the first vertex is equal to the second over the third. For example, $\sin, \tan , \sec$ are 3 consecutive vertices in clockwise order, so this property gives us that $\sin \theta = \frac { \tan \theta} { \sec \theta}$.