Trigonometry: Sine, Cosine, and Tangent

This post is part of a series of posts on Trigonometry. To see all the posts, click on the tag #TrigonometryTutorials below. This is the post you should read before you read this.

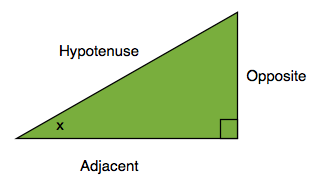
In a Right-angled Triangle, take one of the angles that isn't the right angle and call it $x$. The side that is the longest and is opposite to the right angle is called the Hypotenuse, as you already know.

The side that is next to the angle $x$ and isn't the Hypotenuse is called the Adjacent side, a good way to remember this is that adjacent means "next to"

The remaining side is called the Opposite side, you can remember this because the side is opposite to the angle $x$

Notice if you chose the other angle that isn't $x$ the Adjacent and the Opposite sides would have switched around.

As I have said in my previous post, A Triangle is stable and if you know the 3 angles of a triangle you can find the ratio of the 3 sides of the Triangle. This is what the Trig ratios: Sine, Cosine, and Tangent are for.

Sine, Cosine and Tangent are often abbreviated to $\sin$, $\cos$, and $\tan$ and I will also do so when I refer to them later on.

This is what the Ratios are:

For a Right-Angled Triangle and an angle $x$:

$\sin x = \frac{Opposite}{Hypotenuse}$ $\cos x = \frac{Adjacent}{Hypotenuse}$ $\tan x = \frac{Opposite}{Adjacent}$

A good way to Memorise this is: "SOHCAHTOA", it stands for:

Sine is Opposite divided by Hypotenuse

Cosine is Adjacent divided by Hypotenuse

Tangent is Opposite divided be Adjacent

This is very useful. For example say you have a right angled Triangle and one of the other angles is $30^\circ$. The Hypotenuse is 4 units, what is the length of the Opposite?

Using a Calculator you will find that $\sin 30^\circ = \frac 12$, this means the ratio between the Opposite and the Hypotenuse is $1:2$ since we know the hypotenuse is 4:

$1:2 = Opp : 4$ $Opp = 2$

And we find that the Opposite side has length 2.

There are other Trig Functions which can be used in the same way: Secant ($\sec$), Cosecant ($\csc$), and Cotangent ($\cot$), but these are not used as often:

$\sec x = \frac{Hypotenuse}{Adjacent} = \frac 1{\cos x}$ $\csc x = \frac {Hypotenuse}{Opposite} = \frac 1{\sin x}$ $\cot x = \frac {Adjacent}{Opposite} = \frac 1{\tan x}$

The next post in this series is here