Turn The Pencil Around!

[Warning: This post is quite basic, I mean really basic!]

In an earlier post, we saw a proof without words. On this post we'll see another proof without words. I really loved this when I saw it for the first time and I hope you do too.

Today's topic is really simple: the sum of the angles of a triangle.

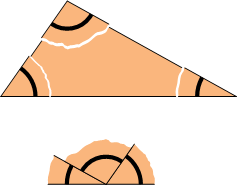
We all know that the sum of the angles of any triangle is equal to $180^{\circ}$ . We've all learned how to prove that in school.

Some of you probably tore off the corners of a triangle to verify that in some point in your life [if you haven't done this, try it now!].

Alt text

But on this post, we're going to do it in a different way, a way that [hopefully] makes us appreciate the beauty in the simplest of things. Let's get on with it!

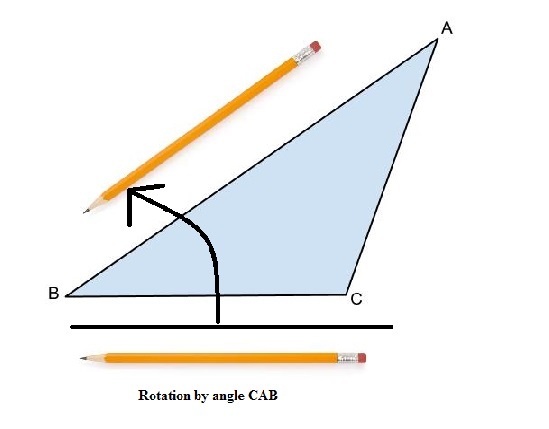
We're going to start with a question? What does it mean when you rotate some thing by $180^{\circ}$ ? If we had a pencil lying horizontally and if we rotated it by $180^\circ$ , what would happen?

Alt text

The picture above demonstrates what a rotation by $180^\circ$ looks like. Keep that in mind.

We're going to start by drawing a triangle and putting a pencil horizontally below it.

Alt text

We have to prove that $\angle CBA+ \angle BAC + \angle ACB=180^\circ$ .

We're going to start by rotating the pencil by $\angle CBA$ .

Alt text

Then by $\angle BAC$ ...

Alt text

And finally, by $\angle ACB$ ...

Alt text

Now if you compare how the pencil was before rotation and what it looks like after being rotated by the angles of triangle $ABC$ , you'll see that the pencil has rotated exactly by $180^\circ$ .

So, $\angle CBA+ \angle BAC + \angle ACB=180^\circ$ [Proved without words!].

This just goes to show that you can look at the simplest of things from a different perspective and enjoy the beauty in them.

Now using the same principle, prove to yourself that the sum of the internal angles of a quadrilateral equals $360^\circ$ . Turn the pencil around!

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Turn The Pencil Around!

Comments