Two Lines Meeting at Infinity

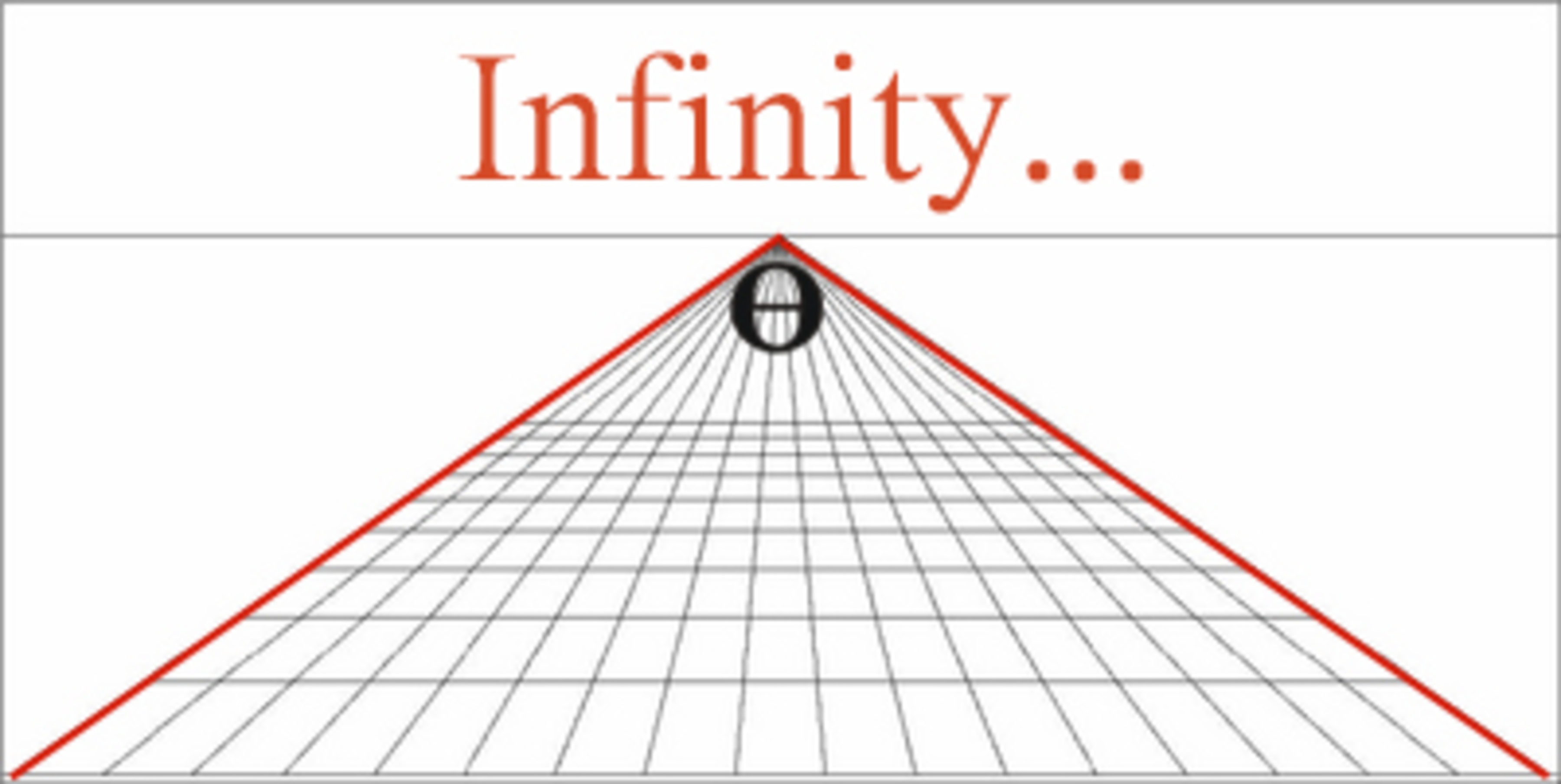
If two lines separated by a finite distance meet at infinity, then what is the angle between them?

In the image example, the lines are separated by a distance of 17 squares, but why should this even have an effect?

Obviously the angle can't be more than 180180 degrees, and since the 33 lines form a triangle the sum of all 33 angles can't be more than 180180 degrees. Is the angle 00 or just infinitesimally small?

Are we even dealing with Euclidean geometry since the lines are meeting at infinity... or do we have to throw the regular rules out the window?

Or perhaps is the angle simply impossible to define?

Share your thoughts please :)

#Geometry #Distance #Angles #Infinity #Note

Note by Alex Delhumeau
5 years, 10 months ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

Visually, it's a matter of perspective, (literally), but mathematically it might be best to analyze this using limits.

First suppose the two red lines meet at a finite distance from the foreground, in effect forming an isosceles triangle with "base" length 1717 and side length x.x. Then by the Cosine rule we have that

172=x2+x2−2x2cos⁡(θ)⟹cos⁡(θ)=1−2892x2.17^{2} = x^{2} + x^{2} - 2x^{2}\cos(\theta) \Longrightarrow \cos(\theta) = 1 - \dfrac{289}{2x^{2}}.

Now as x→∞x \rightarrow \infty we see that cos⁡(θ)→1,\cos(\theta) \rightarrow 1, implying that θ→0.\theta \rightarrow 0.

Brian Charlesworth - 5 years, 10 months ago

We're not dealing with Euclidean geometry. This is about the projective geometry

Agnishom Chattopadhyay - 5 years, 10 months ago

Are we even dealing with Euclidean geometry since the lines are meeting at infinity... or do we have to throw the regular rules out the window?

In affine and Euclidean geometry, it is postulated that two parallel lines DO NOT MEET. You now have to extend your framework to projective geometry, where you can have two lines meeting at a "point in infinity"... because of this, everything you just wrote is meaningless.

A Former Brilliant Member - 2 years, 10 months ago
×

Problem Loading...

Note Loading...

Set Loading...