Updating Archimedes' Method of Approximating π

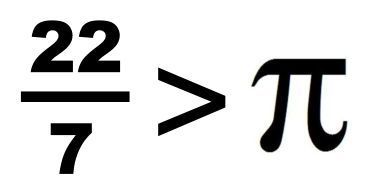
A popular math problem is proving that $22/7$ exceeds $\pi$, without resorting to known values of $\pi$ or approximations by calculator. One method uses certain definite integrals which work out to $22/7$ $-\pi$ which is known to be greater than $0$. But back around 250 BC, Archimedes was the first to prove that $22/7$ exceeds $\pi$, by successive use of the trigonometric identity

$Tan(2x)=\dfrac { 2Tan(x) }{ 1-{ (Tan(x)) }^{ 2 } }$

Starting with the regular hexagon, and doubling the number of sides until he reached a regular polygon of $96$ sides, he was able to show that $22/7$ does indeed exceed $\pi$. Unfortunately, he relied on a series of inequalities in his computations, the notes of which are lost, so we have no complete proof left to us from his works. So, here’s an updated version of his approach that will be an exact proof, beginning with the following diagram

where

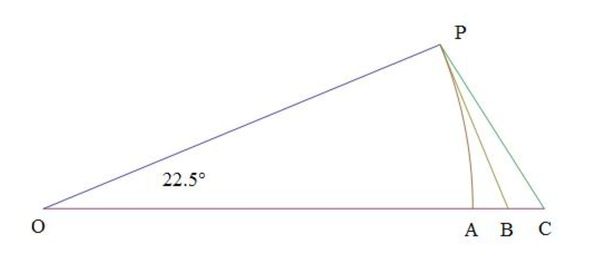
$\angle OPB=90°$
$OP=OA=1$
$OB=Sec(\dfrac { 45° }{ n } )$
$OC=(\dfrac { a }{ b } )(\dfrac { 1 }{ 4n } )Csc(\dfrac{45°}{n})$

In this diagram shown, $n=2$ and $\dfrac { a }{ b } =\dfrac { 25 }{ 7 }$, a very crude apprximation of $\pi$. $\dfrac { a }{ b }$ is selected so that $OC>OB$, so that it is clear that the areas are

$\left[ OPC \right] >\left[ OPB \right] >\left[ OPC \right]$

That is

$(\dfrac { 1 }{ 8n } )(\dfrac { a }{ b } )>(\dfrac { 1 }{ 2 } )Tan(\dfrac { 45° }{ n } )>(\dfrac { 1 }{ 8n } )\pi$

so that if we can prove that for some sufficiently large $n$

$(\dfrac { 1 }{ 4n } )(\dfrac { a }{ b } )>Tan(\dfrac { 45° }{ n } )$

then we've proven that

$\dfrac { a }{ b } >\pi$

Now but there is a delightfully useful trigonometric identity to use for this purpose, which Archimedes didn't have

$Tan(nx)=F(n,Tan(x))=i\dfrac { { (1-iTan(x)) }^{ n }-{ (1+iTan(x)) }^{ n } }{ { (1-iTan(x)) }^{ n }+{ (1+iTan(x)) }^{ n } }$

If $(\dfrac { 1 }{ 4n } )(\dfrac { a }{ b } )>Tan(\dfrac { 45° }{ n } )$, then

$F(n,(\dfrac { 1 }{ 4n } )(\dfrac { a }{ b } ))>F(n,Tan(\dfrac { 45° }{ n } ))$, (a little handwaving here), but since

$F(n,Tan(\dfrac { 45° }{ n } ))=1$, we have

$F(n,(\dfrac { 1 }{ 4n } )(\dfrac { a }{ b } ))>1$

So, for $\dfrac { a }{ b } =\dfrac { 22 }{ 7 }$, all we have to do is to show that for some sufficiently large $n$, let's say $n=24$, which corresponds to the regular $96$ sided polygon Archimedes used

$F(n,(\dfrac { 1 }{ 4n } )(\dfrac { a }{ b } ))=F(24,(\dfrac { 1 }{ 96 } )(\dfrac { 22 }{ 7 } ))>1$

Using that trigonometric identity above, the exact final rational fraction is

$\dfrac { 3070617780371250623172531488874792422422762969087263790473600 }{3070399174588386853835740065608415583799863505007168821897761 }$

Note that the first $6$ digits of the numerator and denominator are

$307061>307039$

which conclusively and exactly proves that $22/7$$>\pi$, without resorting to approximations, without using known computed values of $\pi$, nor infinite series, nor infinite products, nor infinite continued fractions.

Going further, we can let $n=1557$, corresponding to a regular polygon of $6228$ sides, and let $a/b=355/113$, another famous and very accurate approximation. We end up with a rational fraction with a numerator and a denominator both $9105$ digits long, the first $12$ digits of each being

$196554866601 > 196554866571$

thus proving that $355/113>\pi$ as well.

Addendum: Note that as $n\rightarrow \infty$

$Tan(x)=Tan(n(\dfrac { x }{ n } ))=F(n,Tan(\dfrac { x }{ n } ))\approx F(n,(\dfrac { x }{ n } ))$

$F(n,(\dfrac { x }{ n } ))=i\dfrac { { (1-\dfrac { ix }{ n } ) }^{ n }-{ (1+\dfrac { ix }{ n } ) }^{ n } }{ { (1-\dfrac { ix }{ n } ) }^{ n }+{ (1+\dfrac { ix }{ n } ) }^{ n } } =i\dfrac { { e }^{ -ix }-{ e }^{ ix } }{ { e }^{ -ix }+{ e }^{ ix } } =Tan(x)$

which shows the relationship between the exponential form of the $Tan(x)$ function and the trigonometric identity given above for $Tan(nx)$