Vector analysis
Draw a circle in the xy plane .At a few representative points draw the vector v tangent to the circle ,pointing in the clockwise direction.By comparing adjacent vectors,determine the sign of dv sub x/dy and dv sub y/dx .According to cartesian construct of curl that is cross product expansion.What is the direction curl of vector v?Explain how it illustrates the geometrical interpretation of curl.(Here d/dx and d/dy stands for partial derivatives and sub x and y means the x and y component of vector v )
No vote yet
1 vote
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
Define some terms on the unit circle (assuming the tangent vector v is clockwise).
x=cosθy=sinθz=0vx=sinθ=yvy=−cosθ=−xvz=0
Take partial derivatives:
∂y∂vx=1∂x∂vy=−1
Suppose the curl of v is C:
Cx=∂y∂vz−∂z∂vy=0Cy=−∂x∂vz+∂z∂vx=0Cz=∂x∂vy−∂y∂vx=−2
The curl of v is therefore a vector in the −z direction, which agrees with the well-known right-hand rule.
Log in to reply
Thanks a lot you always help me I did the same way by introducing same parameters in the circle it assures that my attempt was right.As author has directly written the vector v even making v sub z non zero but that makes sense because choice of v sub z should be in a manner that C sub x and C sub y should be zero that is derivatives should cancel out to zero in order to make consistency with right hand rule
pls help me with this problem ASAP https://brilliant.org/discussions/thread/potential-energy/
@Steven Chase and @Josh Silverman.Help me with this As shown in the following fig.in the given three arrangements A,B and C where pulleys are ideal,strings are light and inextensible,balls attached at the ends of strings are identical and surfaces where the balls rest are frictionless .Identify the nature of equilibria (i.e stable,unstable or neutral) of the arrangements . @Steven Chase @Josh Silverman Now in the figure shown we have to assume that pulley like in A arrangement is also in B and C arrangement but instead of inclined surfaces concavity in B and convexity in C is introduced as it was super hard for me to draw such figures with mouse .PLS give detailed solutions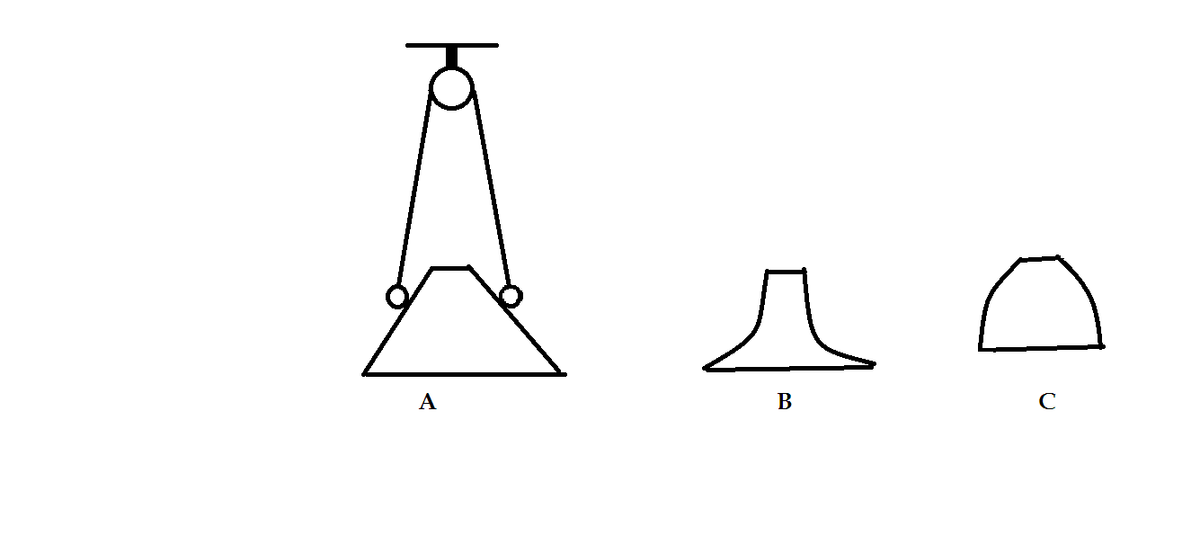
@Steven Chase @Josh Silverman As shown in the following fig.in the given three arrangements A,B and C where pulleys are ideal,strings are light and inextensible,balls attached at the ends of strings are identical and surfaces where the balls rest are frictionless .Identify the nature of equilibria (i.e stable,unstable or neutral) of the arrangements . @Steven Chase @Josh Silverman Now in the figure shown we have to assume that pulley like in A arrangement is also in B and C arrangement but instead of inclined surfaces concavity in B and convexity in C is introduced as it was super hard for me to draw such figures with mouse .PLS give detailed solutions
@Steven Chase Help me with this new problem about equilibria of pulleys
Thanks a lot can you recommend me something on books ,videos,websites,problems regarding the preparation of Indian National Physics Olympiad.
Log in to reply
I haven't been involved with those Olympiads, but there are many on this site who have. I'm sure they could give you some suggestions.
Log in to reply
As shown in the following fig.in the given three arrangements A,B and C where pulleys are ideal,strings are light and inextensible,balls attached at the ends of strings are identical and surfaces where the balls rest are frictionless .Identify the nature of equilibria (i.e stable,unstable or neutral) of the arrangements . @Steven Chase @Josh Silverman Now in the figure shown we have to assume that pulley like in A arrangement is also in B and C arrangement but instead of inclined surfaces concavity in B and convexity in C is introduced as it was super hard for me to draw such figures with mouse .PLS give detailed solutions
@Josh Silverman @Steven Chase
@Steven Chase
Help asap
reply asap